Floyd算法

一种求解“多源最短路”问题的算法

在Floyd算法中，图一般用邻接矩阵存储，边权可正可负（但不允许负环），利用动态规划的思想，逐步求解出任意两点之间的最短距离

int d[N][N],初始为无穷

d[i][j]表示考虑到当前情况下，点i到点j的最短距离

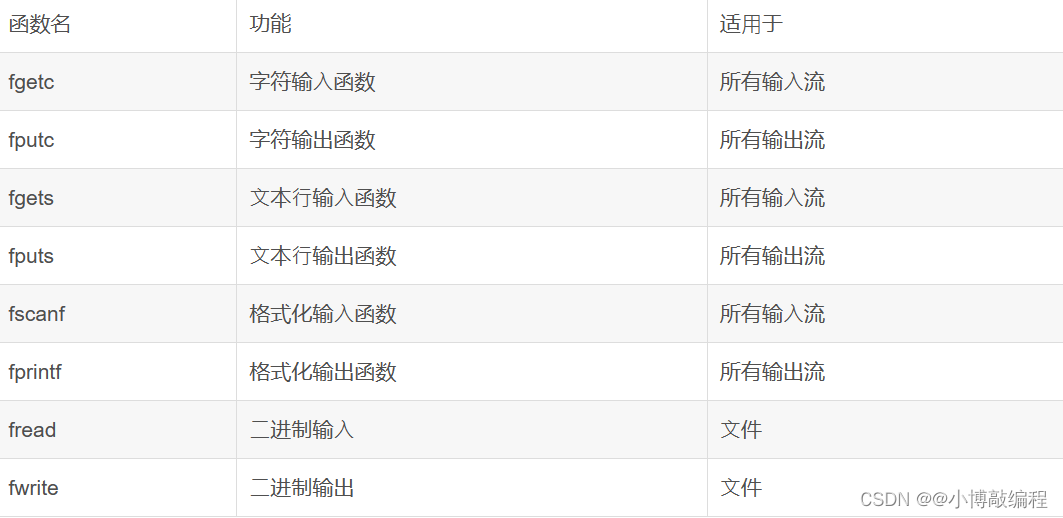
Floyd算法

//注意K作为中转点，必须放最外层

for(in k=1;k<=n;++k)
    for(int i=1;i<=n;++i)
        for(int j=1j<=n;++j)
            if(dep[i][k]!=Long.MAX_VALUE&&dep[k][j]!=Long.MAX_VALUE)
                dep[i][j]=Math.min(dep[i][j],dep[i][k]+dep[k][j]);

只能用来处理n<=500的问题（这也是一个提示，当遇到n<=500的图论问题时，就可以考虑使用Floyd算法）

例题

已知公园有N个景点，景点和景点之间一共有M条道路，小明有Q个观景计划，每个计划包含一个起点st和ed，表示他想从st去到ed，但是小明体力有限，对于每个计划他想走最少的路完成，你可以帮他吗？

输入描述

输入第一行包含三个正整数N,M,Q

第2到M+1行包含三个正整数u,v,w,表示n<->v之间存在一条距离为w的路

第M+2到M+Q-1行每行包含两个正整数st,ed,其含义如题所述

1<=N<=400,1<=M<=N*(N-1)/2,Q<=10^3,1<=u,v,st,ed<=n,1<=w<=10^9

Dijkstra算法

算法需要准备的东西

long dep[N];//dep[i]表示点i距离源点的最短距离。优先队列q以距离从小到大排列

PriorityQueue<long []>q=new PriorityQueue<>((o1,o2)->Long.compare(o1[0],o2[0]));
q.add(new long[]{0L,1L});
while(!q.isEmpty()){

    long []a=q.poll();
    for(int []y:list[(int)a[1]]){
        if(a[0]+y[1]<dep[y[0]]){
            dep[y[0]]=a[0]+y[1];
            q.add(new long [] {dep[y[0]],y[0]});
        
        }
    }
}

例题

小明是蓝桥王国的王子，今天是他登基之日。
在即将成为国王之前，老国王给他出了道题，他想要考验小明是否有
能力管理国家。
题目的内容如下:
蓝桥王国一共有 N个建筑和 M条单向道路，每条道路都连接石两个
建筑，每个建筑都有自己编号，分别为 1~N(其中皇官的编号为1)
国王想让小明回答从皇官到每个建筑的最短路经是多少，但紧张的小
明此时已经无法思考，请你编写程序帮助小明回答国王的考核。

输入描述
输入第一行包含三个正整数 N,M
第2到 M+1行每行包三个正整数 u,v,m，表示u-->v之间存在一条距离为w 的路
1≤N≤3*10^5,1<=m <=10^6, 1< ui,ui<N, 0<=wi< 10^9