通俗说法:

等变性（Equivariance）：对一个输入施加某种变换后所产生的结果同样反应在输出上，说明该变换具有等变性。寻找一个从输入图像到输出类别的映射，这个映射对目标的几何变换(如平移，旋转，投影变换)具有不变性。输入X1，经过平移变换获得X2。f1和f2是经过特征映射的结果，f1经过相同的平移变换后可以得到f2。可以说明这个特征映射操作具有等变性。

 例子：假设我们的变换是将图像向右平移一段距离，我们的函数是检测一个人脸的位置（比如说输出坐标），就是先将图片像右移，接着我们在新图较之原图偏右的位置检测到人脸；则我们先检测人脸再右移或者对原图右移再检测，这两个输出结果是一样的，这个函数就具有等变性。

不变性（Invariance）：意味着即使目标的外观发生了某种变化，但是你依然可以把它识别出来。这对图像分类来说是一种很好的特性，因为我们希望图像中目标无论是被平移，被旋转，还是被缩放，甚至是不同的光照条件、视角，都可以被成功地识别出来。

为什么具有cnn具有不变性？

不严谨的说法是卷积操作+池化操作约等于不变性

卷积：简单地说，图像经过平移，相应的特征图上的表达也是平移的。

 

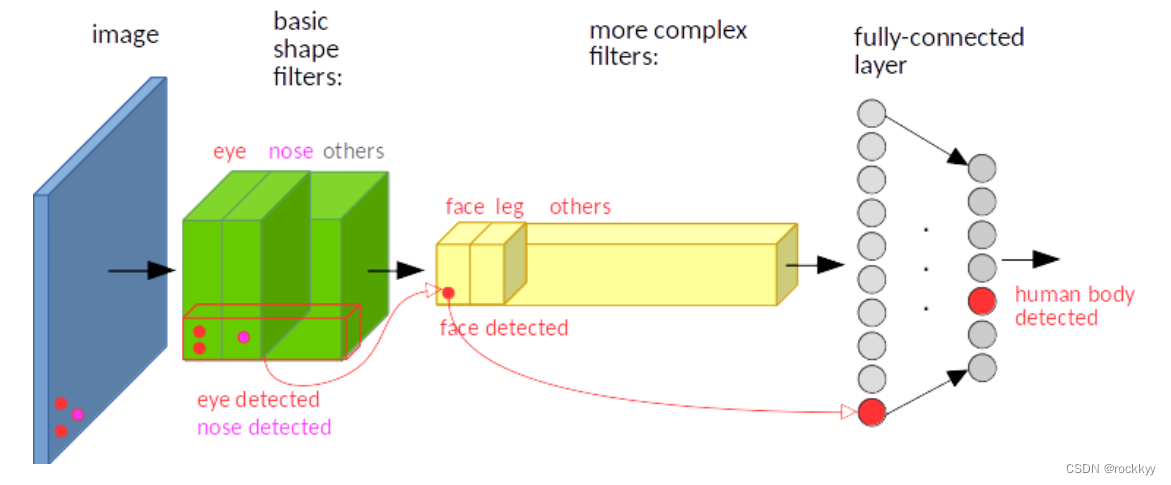
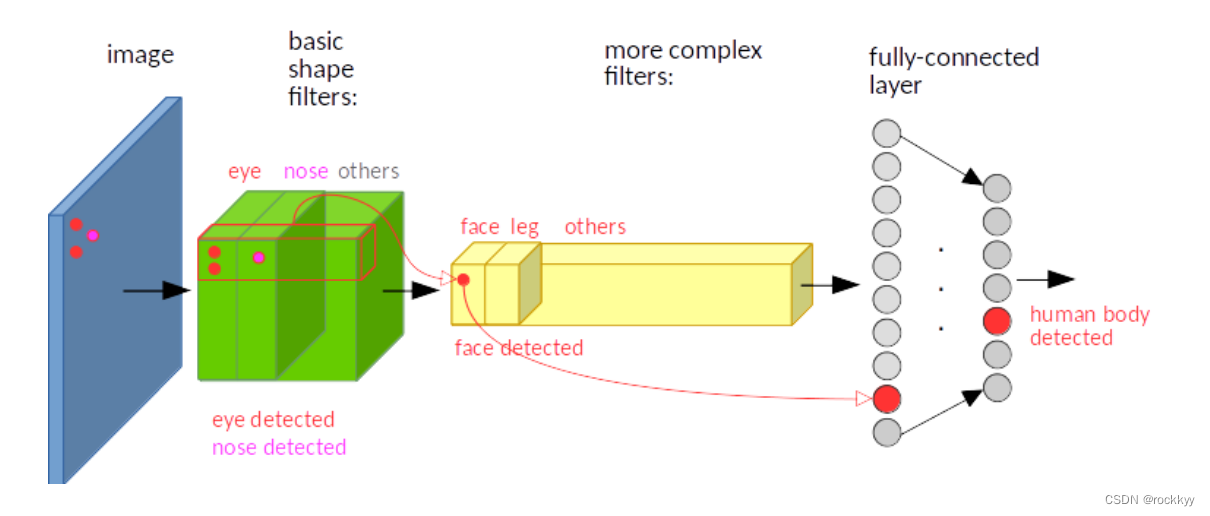
 池化：比如最大池化，它返回感受野中的最大值，如果最大值被移动了，但是仍然在这个感受野中，那么池化层也仍然会输出相同的最大值。这就有点平移不变的意思了。

Reference：

卷积神经网络为什么具有平移不变性？ | Tina's Blog (zhangting2020.github.io)

What is translation equivariance, and why do we use convolutions to get it? | by Christian Wolf | Medium