LCA(最近公共祖先)
定义:有根树的两个节点u,v,他们的LCA是一个节点x,其中x是他们的公共祖先并且X的深度尽可能大。
法1---Tarjan算法:
核心:DFS+并查集
在并查集中建立仅有u的集合,设该集合祖先为u,对于他的每一个孩子v:dfs(v)
合并v到父节点u的集合,设置u为已遍历。
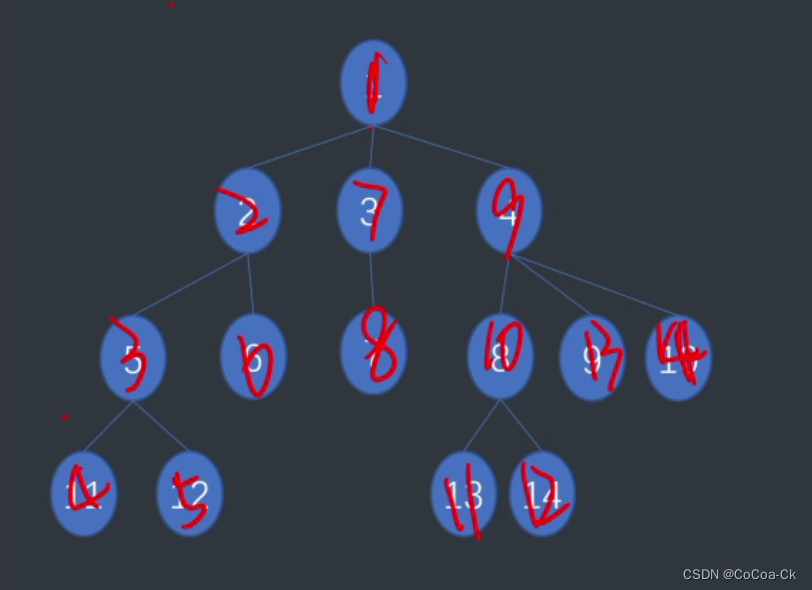
有点抽象,来看看图例吧:
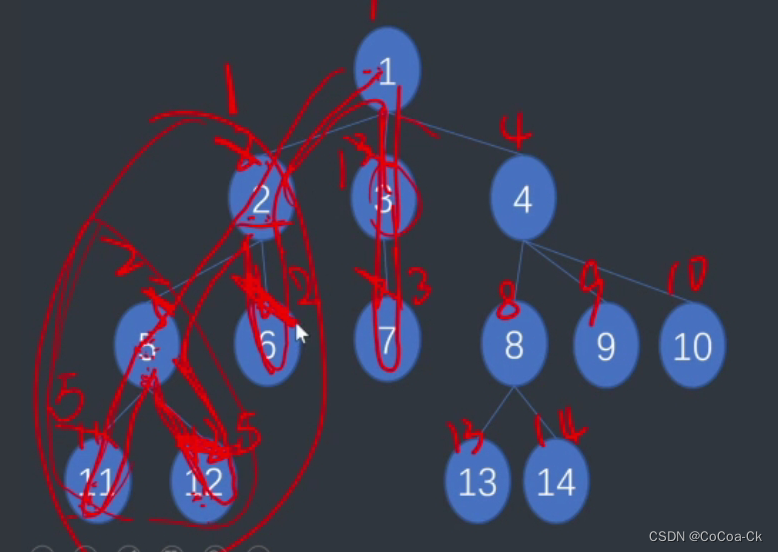
首先,一开始每一个点的fa都是自己,然后遍历到11,它没有儿子,设置11为已遍历并指向5,然后到12,此时若有11与12的询问就是11的fa,标记12并到5,5指2并标记,依次类推即可
注意,这要把所有询问提前记录下来(即离线操作)
下面是模板代码:
#include<bits/stdc++.h>
using namespace std;
int fa[100000];
vector<int> a[100000];
int que[1000][1000];
bool vis[100000];
int find(int x){
if(x==fa[x]) return x;
return fa[x]=find(fa[x]);
}
void merge(int x,int y){
x=find(x);
y=find(y);
fa[x]=y;
}
void dfs(int x,int fa){
for(int i=0;i<a[x].size();i++){
int y=a[x][i];
dfs(y,x);
merge(y,x);
}
vis[x]=1;
for(int i=1;i<=n;i++){
if(vis[i]&&que[x][i]){
int tmp=find(i);
cnt[tmp]+=que[x][i];
que[x][i]=que[i][x]=0;
}
}
}法2--通过DFS序转化成RMQ问题
对有根树DFS,按照遍历顺序记录2*N-1的序列即欧拉序列
我们发现两个数(u,v)(前面的先出现)的LCA就是最后一次出现的u和第一次出现的v中间的数就是从u--v的路径,而其中深度最低(包含自己)的就是其LCA。
因此我们求一个min即可,其中我们为了方便可以从第一次出现的u开始(其子树不影响)
怎么求RMQ?
1.线段树。
2.ST。
线段树大家都知道,那么就看一下ST吧
In a word,ST就是DP+倍增
我们用f[i][j]表示[i,i+2^j-1]的min,f[i][0]=a[i],因此,f[i][j]=min(f[i][j-1],f[i+2^(j-1),][j-1])
当我们要查询时,对于[10,20],我们可以先得到[10,18]的min与[19,20](根据2进制看)
我们也可以[10,18]以及[12,20]。
下面是模板代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
int b[N],dp[N][N];
void rmq_st(int n){
for(int i=1;i<=n;i++) dp[i][0]=b[i];
int m=(int)(log(1.0*n)/log(2.0));
for(int j=1;j<=m;j++){
int t=n-(1<<j)+1;
for(int i=1;i<=t;i++){
dp[i][j]=min(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);
}
}
}
int rmp_find(int l,int r){
int k=(int)(log(1.0*(r-l+1))/log(2.0));
return min(dp[l][k],dp[r-(1<<k)+1][k]);
}接下来我们看看如何编号。
我们用DFN序编号即可以(直接按照深度存的话对于一个深度可能有很多对应)
下面是实现代码:
void dfs(int x,int fa){
int tmp=++num;
b[++cnt]=tmp;//以DFS代替的欧拉序
f[tmp]=x;//实现从DFS序到真实点的映射
first[x]=cnt;//记录x第一次出现的位置
for(int i=head[x];i!=-1;i=edge[i].next){
int v=edge[i].dian;
if(v==fa) continue;
dfs(v,x);
b[++cnt]=tmp;
}
}
int LCA(int a,int b){
if(first[a]>first[b]) swap(a,b);
int k=rmq_find(first[a],first[b]);
return f[k];
}下面介绍一下如何求两个点的距离算是应用吧:
每一个点到根的距离-2*LCA到根的距离。
下面介绍介绍常见的3种“dfs序”
欧拉序:每经过一点记录一次的序列
DFS序:记录进栈与出栈的序列。
DFN序:只记录进栈的序列。
对于这个图:
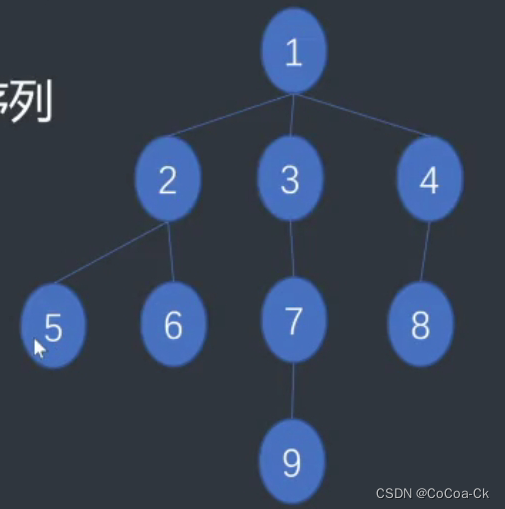
欧拉序:12552.....DFS序:1255662379.。。。DFN序(时间戳):12563....
对于时间戳:
125637948,我们记录一下每一个子树的最大时间(即最后进栈),我们发现对于256,379,任何一个子树在其中都是连着并不重复出现的,而当我们知道一个子树的最大时间就知道了对应的区间。
这有什么用呢?
在树上1.修改x变成Y,2.查以x为根的子树的权值和。
这就转化成了区间和的问题,对DFN序再用树状数组维护即可。
我们来个应用吧:
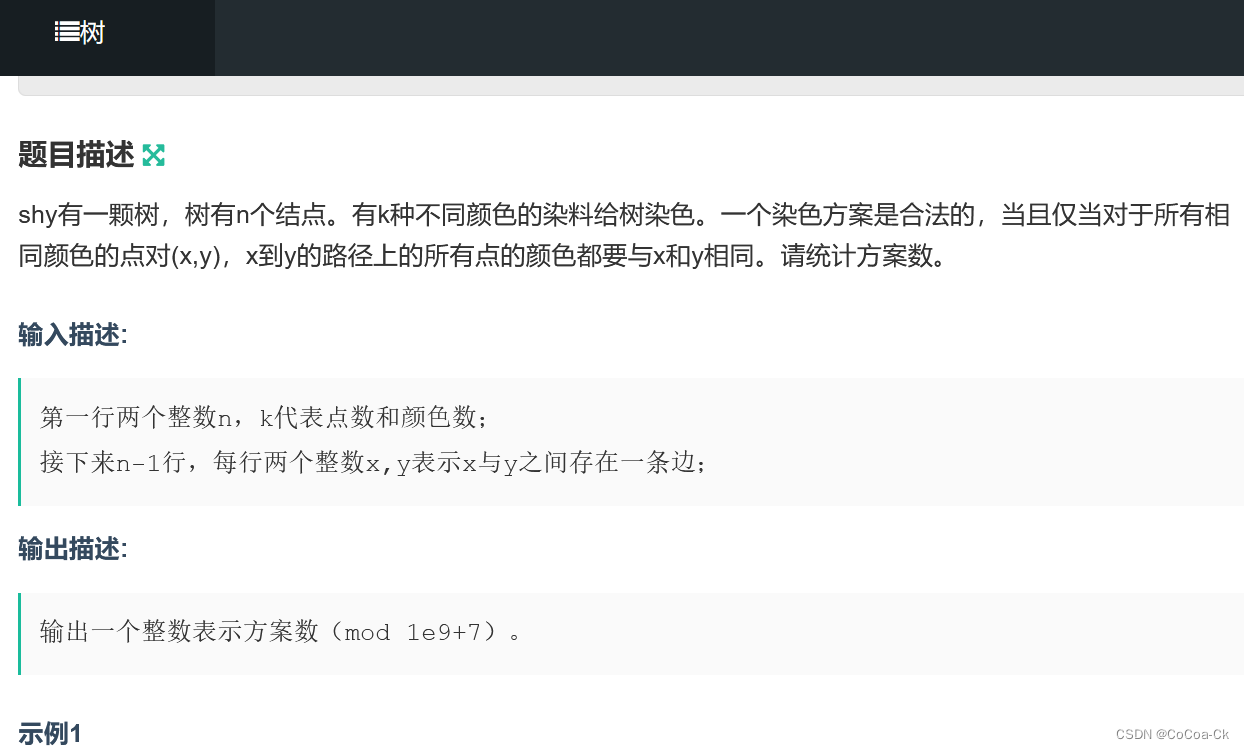
我们先按DFN,我们发现一个点要么跟父亲一样,要么是一个从来没有出现的点,这个就是合法的,于是我们令dp[i][j]表示走到i时用了j种颜色的方案数,易得状态转移方程:
dp[i][j]=dp[i-1][j]+dp[i-1][j-1]*(k-j+1).
下面是AC代码:
#include<bits/stdc++.h>
#define mod 1000000007
using namespace std;
int n,y,k,x;
long long dp[400][400];
int main(){
cin>>n>>k;
dp[0][0]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=k;j++){
dp[i][j]=(dp[i-1][j]+dp[i-1][j-1]*(k-j+1))%mod;
}
}
long long ans=0;
for(int i=1;i<=k;i++) ans=(ans+dp[n][i])%mod;
cout<<ans;
}