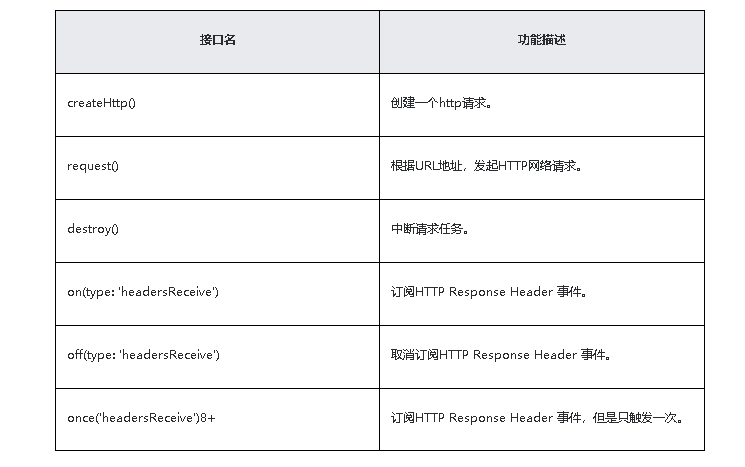
有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ,其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。
一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后,可以无限地前进。
给你一个数组 points ,返回引爆所有气球所必须射出的 最小 弓箭数 。
示例 1:
输入:points = [[10,16],[2,8],[1,6],[7,12]] 输出:2 解释:气球可以用2支箭来爆破: -在x = 6处射出箭,击破气球[2,8]和[1,6]。 -在x = 11处发射箭,击破气球[10,16]和[7,12]。
示例 2:
输入:points = [[1,2],[3,4],[5,6],[7,8]] 输出:4 解释:每个气球需要射出一支箭,总共需要4支箭。
示例 3:
输入:points = [[1,2],[2,3],[3,4],[4,5]] 输出:2 解释:气球可以用2支箭来爆破: - 在x = 2处发射箭,击破气球[1,2]和[2,3]。 - 在x = 4处射出箭,击破气球[3,4]和[4,5]。
提示:
1 <= points.length <=points[i].length == 2-<= xstart < xend <=
- 1
对于示例 1 的一个简单图示:

思路:
采用贪心思路。局部最优:遇到重合的气球就只用一支箭。全局最优:引爆所有气球的箭数最少。
要怎么确定气球是否重合呢?将气球按照 xstart 升序排列,然后比较当前气球的 xstart 和前一个气球的 xend 是否有重合,如果有的话,则说明这两个气球可以用一支箭引爆,如果没有重合的话,则箭的数量加一支,来引爆当前气球。
需要注意的是,如果当前气球和前一个气球有重合,则需要更新 已重合的气球中的最小右边界,下一次比较时,就用下一个气球的 xstart 与 已重合的气球中的最小右边界 xend 进行比较,如果有重合,则继续更新 已重合气球中的最小右边界;如果没有重合,则需要加一支箭来引爆 下一个气球。
代码:
class Solution {
public int findMinArrowShots(int[][] points) {
//按照 xstart 进行升序排序
//利用 Integer.compare 避免溢出
Arrays.sort(points,(o1,o2)->{
return Integer.compare(o1[0],o2[0]);
});
//因为 points 不为空,所以至少需要一支箭
int count =1;
for(int i=1;i<points.length;i++){
if(points[i][0]>points[i-1][1]){//此时说明前后两支箭不重合,注意没有等于,因为等于的话相当于重合。
count++;//需要多一支箭来引爆 points[i] 对应的气球
}
else{//此时说明 points[i] 与 points[i-1] 重合
// 需要更新最小的重合的右边界
points[i][1] = Math.min(points[i][1],points[i-1][1]);
}
}
return count;
}
}参考:代码随想录