1.5-数组-059. 螺旋矩阵 II★★

news2024/10/5 17:27:49

59. 螺旋矩阵II ★★

力扣题目链接，给你一个正整数 n ，生成一个包含 1 到 $n^2$ 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。1 <= n <= 20

示例 1：

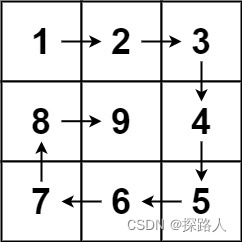
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

思路

本题没有什么算法，就是模拟过程，但较考察代码的掌控能力。 参考数组：每次遇到二分法，都是一看就会，一写就废中讲解的二分法，一定要坚持 循环不变量原则。

模拟顺时针画矩阵的过程:

填充上行从左到右
填充右列从上到下
填充下行从右到左
填充左列从下到上

由外向内一圈一圈画下去。

画每条边都要坚持一致的左闭右开、或左开右闭原则，这样一圈才能按照统一的规则画下来。这里按左闭右开，画一圈，大家看看：

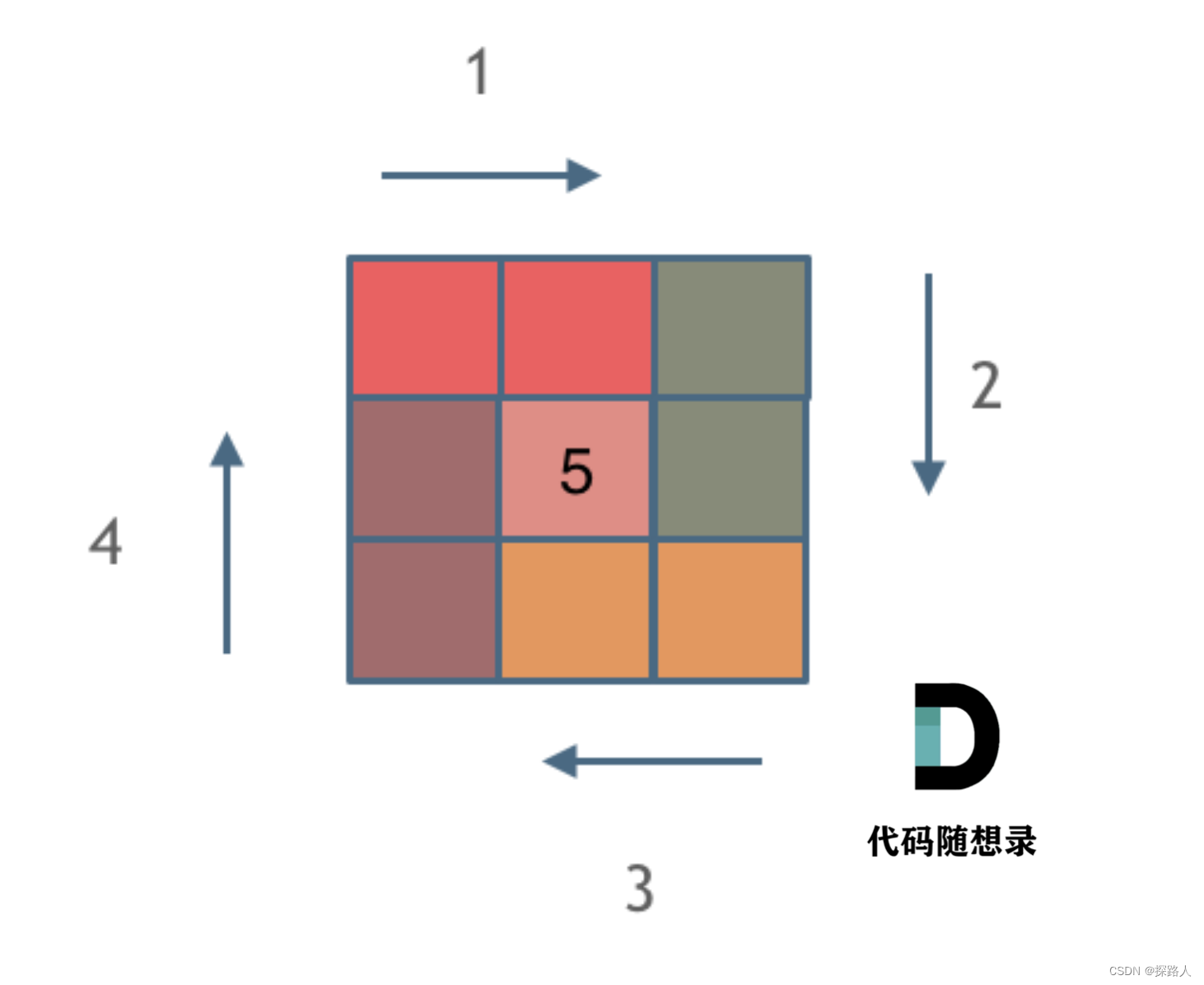
在这里插入图片描述

本地练习

pub struct Solution;

impl Solution {
    pub fn generate_matrix(n: i32) -> Vec<Vec<i32>> {
        
    }
}

fn main() {
    let res = [4, 3, 1].iter().map(|&x| Solution::generate_matrix(x)).collect::<Vec<Vec<Vec<_>>>>();
    println!("{:?}: {:?}", vec![
        vec![vec![1, 2, 3, 4], vec![12, 13, 14, 5], vec![11, 16, 15, 6], vec![10, 9, 8, 7]],
        vec![vec![1, 2, 3], vec![8, 9, 4], vec![7, 6, 5]],
        vec![vec![1]],
    ] == res, res);
}

Rust答案

impl Solution {
    pub fn generate_matrix(n: i32) -> Vec<Vec<i32>> {
        let mut res = vec![vec![0; n as usize]; n as usize]; // 二维矩阵存储结果
        let (mut start_x, mut start_y) = (0, 0);    // 循环每一圈的起始位置
        let mut loop_idx = n / 2;    // 循环几圈，例如 n 为 3，则 loop = 1 只循环一圈
        // let mid = loop_idx as usize; // 矩阵中心，n % 2 > 0 时有效，n = 3，中心为(1，1)，n = 5，中心为(2, 2)
        let mut count = 1;  // 用来给矩阵中每一个格子赋值
        let mut offset = 1; // 控制每条边遍历的长度，每完成一圈，增加收缩两位（左右/上下 各一位）
        while loop_idx > 0 {
            let (mut i, mut j) = (start_x, start_y);

            while j < (start_y + (n as usize) - offset) {
                res[i][j] = count;
                count += 1;
                j += 1;
            }

            while i < (start_x + (n as usize) - offset) {
                res[i][j] = count;
                count += 1;
                i += 1;
            }

            while j > start_y {
                res[i][j] = count;
                count += 1;
                j -= 1;
            }

            while i > start_x {
                res[i][j] = count;
                count += 1;
                i -= 1;
            }

            // 第二圈开始时，起始位置各自加1，例如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)
            start_x += 1;
            start_y += 1;
            offset += 2;    // 向内圈进发时，每进一圈增加收缩的步进
            loop_idx -= 1;  // 剩余圈数，每次减 1
        }

        if n % 2 == 1 {     // n为奇数时（对2取模有余数时），说明有中心点，需要单独给中间位置赋值
            let mid = (n / 2) as usize; // 矩阵中心，n % 2 > 0 时有效，n = 3，中心为(1，1)，n = 5，中心为(2, 2)
            res[mid][mid] = count;
        }
        res
    }
}