机器学习优化算法（深度学习）

预备知识

梯度

Hessian 矩阵（海森矩阵，或者黑塞矩阵）

拉格朗日中值定理

柯西中值定理

泰勒公式

黑塞矩阵（Hessian矩阵）

Jacobi 矩阵

优化方法

梯度下降法（Gradient Descent）

随机梯度下降法（Stochastic Gradient Descent, SGD）

原理

优点

缺点

核心思路代码体现

运行结果

动量法（Momentum）和Nesterov 动量法

动量法

原理

优点

缺点

牛顿动量（Nesterov）算法

原理

和动量法的区别

Adam（Adaptive Moment Estimation）

原理

代码

AdaGrad（Adaptive Gradient Algorithm）和RMSprop

Adagrad方法

原理

优缺点

RMSprop

原理

牛顿法（Newton's Method）和拟牛顿法（Quasi-Newton Methods）

原理

代码

共轭梯度法（Conjugate Gradient）

原理

代码

SA（Simulated Annealing）

原理

代码

AC-SA（Adaptive Clustering-based Simulated Annealing）

PSO（Particle Swarm Optimization）

预备知识

梯度

关于梯度，可以看我的这篇博客，这里就不多加阐述了，梯度

Hessian 矩阵（海森矩阵，或者黑塞矩阵）

我们先看一下百科的定义：

很抽象对吧，别着急，慢慢来，我们要先了解一下泰勒展开式：

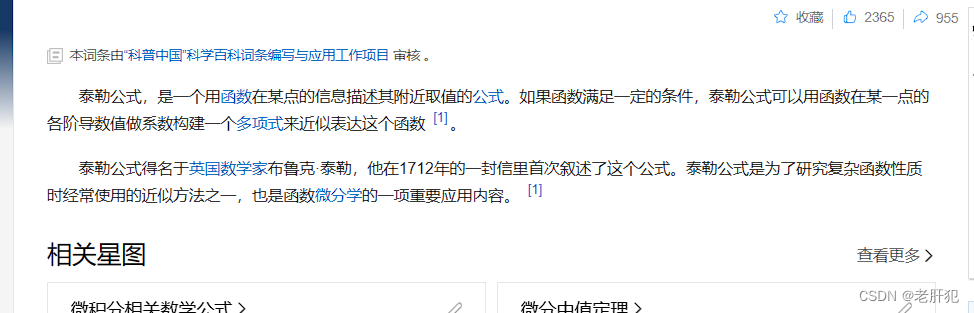
什么是泰勒展开式呢？

这就需要了解一下柯西中值定理了：

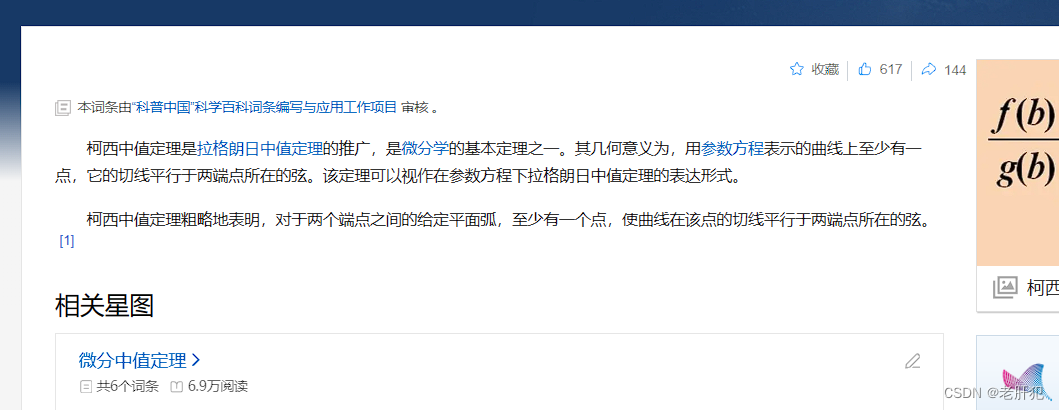
在了解柯西中值定理之前，我们要先了解拉格朗日中值定理：

拉格朗日中值定理

什么意思呢？

就是如果函数f(x)在闭区间上[a,b]连续，在开区间(a,b)上可导，那么在开区间(a,b)内至少存在一点ξ使得f '(ξ)=(f(b)-f(a))/(b-a)。

在几何意义上表示为：

在知道了拉格朗日中值定理后，我们就可以了解柯西中值定理了，柯西中值定理就是拉格朗日中值定理的推广。

柯西中值定理

它的原理如下：

几何意义：

怎么理解呢？我的理解是这样的，我们的百科是通过参数方程的形式，用参数方程的确也方便一些（本人关于参数方程的部分很多都忘却了）

什么是参数方程，这是知乎网友给出的答案：

放到我们这里来也就是说，我们把x换成t那么这个不等式的参数方程为：

我们会得到他的图像：

所以

所以就是我们百科给的那样的几何意义：曲线上至少有一点，它的切线的斜率与割线斜率是相等的。

泰勒公式

接下来我们就要说一下泰勒公式了：

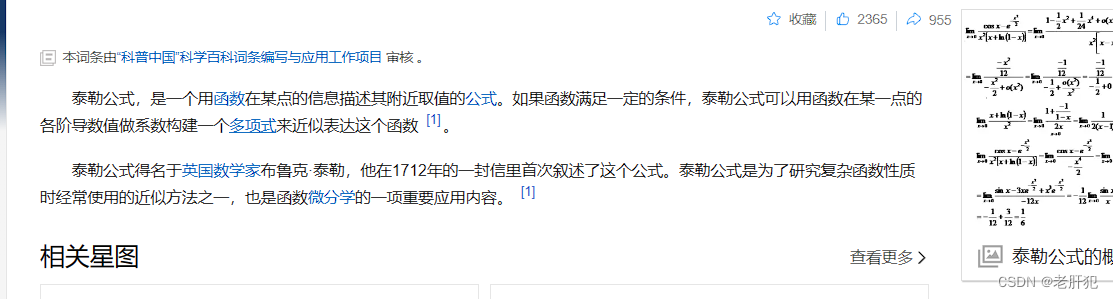
这是百科给的定义，下面是

其实我也不想直接copy百科，可是这个公式确实就是这样的

泰勒公式的几何意义是利用多项式函数来逼近原函数，由于多项式函数可以任意次求导，易于计算，且便于求解极值或者判断函数的性质，因此可以通过泰勒公式获取函数的信息，同时，对于这种近似，必须提供误差分析，来提供近似的可靠性

黑塞矩阵（Hessian矩阵）

黑塞矩阵就是根据泰勒展开式得来的，这一块，百科确实写的不错，我们看百科

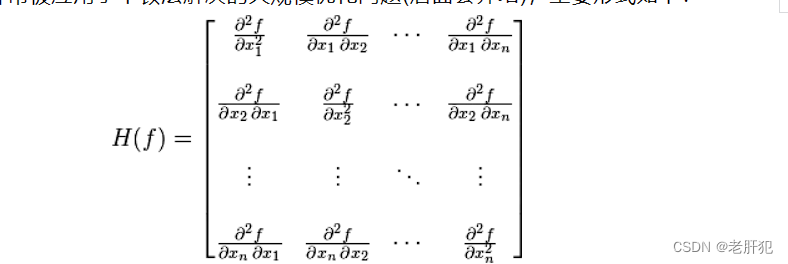
前面明白的话，这里应该就没问题了

Jacobi 矩阵

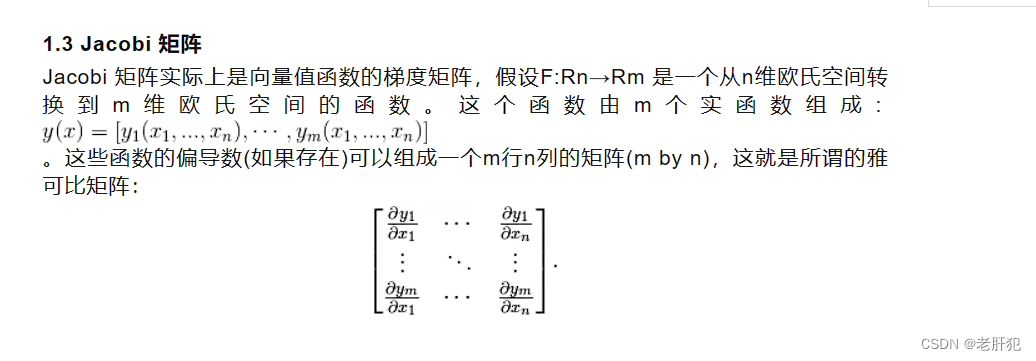
这个矩阵就是这个样子的，至于推导过程，这里就不多加阐述了。

优化方法

梯度下降法（Gradient Descent）

详情请点击梯度下降法

随机梯度下降法（Stochastic Gradient Descent, SGD）

原理

随机梯度下降法一般都称之为SGD，是在梯度下降算法效率上做了优化，也就是基本原理和梯度下降相同。

他的随机体现在了，不使用所有的样本计算当前的梯度，而是随机梯度下降是在每次迭代时使用一个样本来对参数进行更新

优点

这样每次都会得到和全部样本的梯度方向相似的方向，从而进行梯度下降，最后的结果虽然和直接全部样本的梯度进行下降来比准确度什么的都要小一些，但是这样会更快收敛。且训练集通常存在冗余，大量样本都对梯度做出了非常相似的贡献。此时基于小批量样本估计梯度的策略也能够计算正确的梯度，但是节省了大量时间。

缺点

SGD的缺点是容易陷入局部最优解，可结合其他优化算法如动量法或Adam等来提高收敛效果

核心思路代码体现

import  torch
import numpy as np
from matplotlib import pyplot as plt, font_manager
print('随机梯度下降-----------')


# 定义损失函数
def loss_function(w, X, y):
    return np.mean(np.sum(np.square(X.dot(w) - y)))


# 定义梯度函数
def gradient(w, X, y):
    return np.mean(X.T.dot((X.dot(w) - y)) )


# 定义SGD优化器
def sgd(X, y, learning_rate=0.01, epochs=100):
    n_features = X.shape[1]
    w = np.zeros(n_features)
    for epoch in range(epochs):
        for i in range(len(X)):
            grad = gradient(w, X[i], y[i])
            w -= learning_rate * grad
        print("Epoch %d loss: %f" % (epoch + 1, loss_function(w, X, y)))
    return w
X=np.array([[0.180,0.001*1,0.001*4],[0.100,0.001*2,0.001*2],
            [0.160,0.001*3,0.001*4],[0.080,0.001*4,0.001*2],
            [0.090,0.001*5,0.001*2],[0.110,0.001*6,0.001*3],
            [0.120,0.001*7,0.001*3],[0.170,0.00*8,0.001*4],
            [0.150,0.001*9,0.001*4],[0.140,0.001*10,0.001*4],
            [0.130,0.001*11,0.001*3]])
y = np.array([+1, -1, +1, -1, -1, -1, -1, +1, +1, +1, -1])
sgd(X,y)

运行结果

D:\Anaconda3\envs\pytorch\python.exe D:\learn_pytorch\学习过程\第三周的代码\代码一.py 
随机梯度下降-----------
Epoch 1 loss: 10.999823
Epoch 2 loss: 10.999646
Epoch 3 loss: 10.999470
Epoch 4 loss: 10.999293
Epoch 5 loss: 10.999118
Epoch 6 loss: 10.998942
Epoch 7 loss: 10.998766
Epoch 8 loss: 10.998591
Epoch 9 loss: 10.998416
Epoch 10 loss: 10.998242
Epoch 11 loss: 10.998067
Epoch 12 loss: 10.997893
Epoch 13 loss: 10.997719
Epoch 14 loss: 10.997545
Epoch 15 loss: 10.997372
Epoch 16 loss: 10.997199
Epoch 17 loss: 10.997026
Epoch 18 loss: 10.996853
Epoch 19 loss: 10.996681
Epoch 20 loss: 10.996509
Epoch 21 loss: 10.996337
Epoch 22 loss: 10.996166
Epoch 23 loss: 10.995994
Epoch 24 loss: 10.995823
Epoch 25 loss: 10.995652
Epoch 26 loss: 10.995482
Epoch 27 loss: 10.995311
Epoch 28 loss: 10.995141
Epoch 29 loss: 10.994971
Epoch 30 loss: 10.994802
Epoch 31 loss: 10.994632
Epoch 32 loss: 10.994463
Epoch 33 loss: 10.994295
Epoch 34 loss: 10.994126
Epoch 35 loss: 10.993958
Epoch 36 loss: 10.993790
Epoch 37 loss: 10.993622
Epoch 38 loss: 10.993454
Epoch 39 loss: 10.993287
Epoch 40 loss: 10.993120
Epoch 41 loss: 10.992953
Epoch 42 loss: 10.992786
Epoch 43 loss: 10.992620
Epoch 44 loss: 10.992454
Epoch 45 loss: 10.992288
Epoch 46 loss: 10.992122
Epoch 47 loss: 10.991957
Epoch 48 loss: 10.991792
Epoch 49 loss: 10.991627
Epoch 50 loss: 10.991462
Epoch 51 loss: 10.991298
Epoch 52 loss: 10.991134
Epoch 53 loss: 10.990970
Epoch 54 loss: 10.990806
Epoch 55 loss: 10.990643
Epoch 56 loss: 10.990480
Epoch 57 loss: 10.990317
Epoch 58 loss: 10.990154
Epoch 59 loss: 10.989992
Epoch 60 loss: 10.989830
Epoch 61 loss: 10.989668
Epoch 62 loss: 10.989506
Epoch 63 loss: 10.989344
Epoch 64 loss: 10.989183
Epoch 65 loss: 10.989022
Epoch 66 loss: 10.988861
Epoch 67 loss: 10.988701
Epoch 68 loss: 10.988540
Epoch 69 loss: 10.988380
Epoch 70 loss: 10.988221
Epoch 71 loss: 10.988061
Epoch 72 loss: 10.987902
Epoch 73 loss: 10.987742
Epoch 74 loss: 10.987584
Epoch 75 loss: 10.987425
Epoch 76 loss: 10.987267
Epoch 77 loss: 10.987108
Epoch 78 loss: 10.986950
Epoch 79 loss: 10.986793
Epoch 80 loss: 10.986635
Epoch 81 loss: 10.986478
Epoch 82 loss: 10.986321
Epoch 83 loss: 10.986164
Epoch 84 loss: 10.986008
Epoch 85 loss: 10.985851
Epoch 86 loss: 10.985695
Epoch 87 loss: 10.985539
Epoch 88 loss: 10.985384
Epoch 89 loss: 10.985228
Epoch 90 loss: 10.985073
Epoch 91 loss: 10.984918
Epoch 92 loss: 10.984764
Epoch 93 loss: 10.984609
Epoch 94 loss: 10.984455
Epoch 95 loss: 10.984301
Epoch 96 loss: 10.984147
Epoch 97 loss: 10.983994
Epoch 98 loss: 10.983840
Epoch 99 loss: 10.983687
Epoch 100 loss: 10.983534

进程已结束,退出代码0

这里只是简单训练了100次，可以看出来损失函数是不断下降的

动量法（Momentum）和Nesterov 动量法

动量法

原理

动量法是梯度下降算法的一种改进，它引入了动量的概念以加速目标函数收敛过程并减小震荡。动量法的基本思想是在更新参数的过程中，不仅考虑当前的梯度方向，同时也考虑历史累积的梯度信息。

折扣因子表示历史梯度的影响力，越大代表影响力越大。直观上来说，要是当前时刻的梯度与历史梯度方向趋近，这种趋势会在当前时刻加强，否则当前时刻的梯度方向减弱。这一点从上面也可以看出来。

优点

考虑历史梯度，将会引导参数朝着最优值更快收敛

缺点

当折扣率变大时，对历史梯度的记忆更多，我们的参数值变化时容易“震荡”，也就是幅度比较大的“来回变化”

牛顿动量（Nesterov）算法

原理

为了解决“震荡”问题，我们才有了牛顿动量法。引入了一个动量单位，这里面的“贝塔”也是一个折扣因子

和动量法的区别

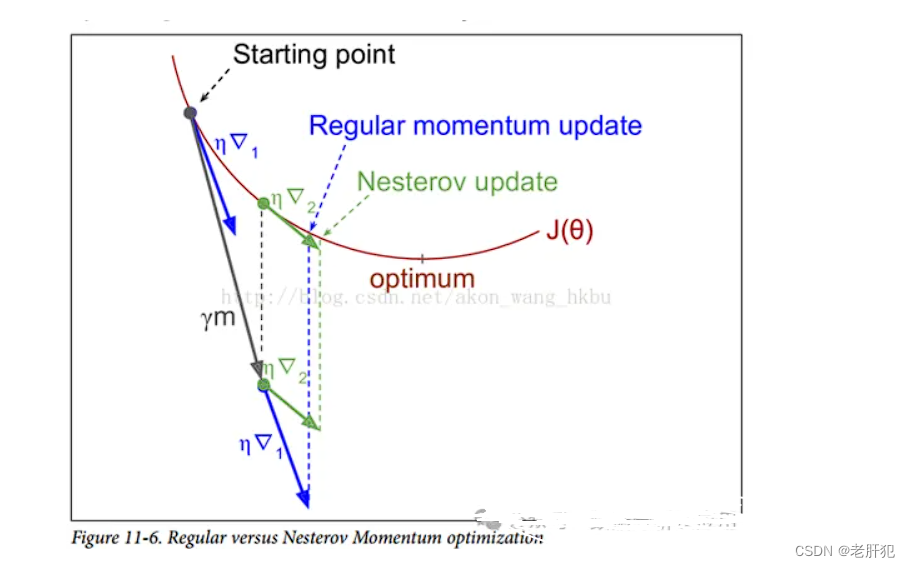
倒三角1表示的是动量法，倒三角2就是牛顿动量法，可以看到牛顿动量法比普通的动量法更快的收敛，并且幅度小，会减弱“震荡”

Adam（Adaptive Moment Estimation）

原理

Adam是最常用的优化算法之一，是一种自适应学习率的优化算法，能计算每个参数的自适应学习率。

Adam 算法的关键在于同时计算梯度的一阶矩（均值）和二阶矩（未中心的方差）的指数移动平均，并对它们进行偏差校正，以确保在训练初期时梯度估计不会偏向于 0。

二阶矩的计算式就是方差的计算式没有减去均值，也就是这样的： $\frac{\sum_{i}^{n}Xi^{2}}{n}$

（图片内容来自网络，侵权必删）

代码

import torch
import torch.optim as optim
import numpy as np
print("Adam（Adaptive Moment Estimation）--------------------------------")
x = torch.Tensor([[0.18],[0.1], [0.16], [0.08], [0.09], [0.11], [0.12], [0.17], [0.15], [0.14], [0.13]])
y = torch.Tensor([[0.18], [0.1], [0.16], [0.08], [0.09], [0.11], [0.12], [0.17], [0.15], [0.14], [0.13]])
bath = 5
epoches = 100
listw = []
listl = []
lista = []
a = 0
loss = 0
class LNode(torch.nn.Module):
    def __init__(self):
        super(LNode,self).__init__()
        self.linear=torch.nn.Linear(1,1)
    def forward(self,x):
        predict_y = self.linear(x)
        return predict_y
module=LNode()
# 定义损失函数和梯度函数（这里使用PyTorch的自动梯度计算）
loss_function = torch.nn.MSELoss()  # 均方误差损失函数
gradient = torch.autograd.grad  # 自动梯度计算函数

# 定义Adam优化器（这里使用了PyTorch的Adam类）
optimizer = optim.Adam([torch.Tensor([0.])], lr=0.01)  # 学习率设置为0.01，初始权重为0向量（注意：PyTorch中优化器的权重参数需要是tensor对象）
for i1 in range(1,bath):
    for i2 in range(1,epoches):
        a=a+1
        pre_y = module(x)
        optimizer.zero_grad()  # 清除历史梯度信息（如果使用其他优化器，可能需要手动清除梯度）
        loss = loss_function( pre_y, y)  # 计算损失函数值（这里使用了PyTorch的Tensor类，模拟了线性回归问题的数据和目标）
        loss.backward()  # 反向传播计算梯度（这里使用了PyTorch的backward方法）
        optimizer.step()  # 更新权重（这里使用了PyTorch的step方法）
    print('第{1}次训练，loss:{0}'.format(loss, a))
    listl.append(loss.data)
    lista.append(a)
    print('w:', module.linear.weight.data.item())
    print('b:', module.linear.bias.data.item())
    listw.append(module.linear.weight.data.item())

运行结果

D:\Anaconda3\envs\pytorch\python.exe D:\learn_pytorch\学习过程\第三周的代码\代码三.py 
Adam（Adaptive Moment Estimation）--------------------------------
第99次训练，loss:0.0038715994451195
w: -0.7687562704086304
b: 0.20267844200134277
第198次训练，loss:0.0038715994451195
w: -0.7687562704086304
b: 0.20267844200134277
第297次训练，loss:0.0038715994451195
w: -0.7687562704086304
b: 0.20267844200134277
第396次训练，loss:0.0038715994451195
w: -0.7687562704086304
b: 0.20267844200134277

进程已结束,退出代码0

AdaGrad（Adaptive Gradient Algorithm）和RMSprop

Adagrad方法

原理

首先了解一下稀疏数据：

稀疏数据是指，数据框中绝大多数数值缺失或者为零的数据。

稀疏参数：稀疏的数据对应的参数

Adagrad方法是通过参数来调整合适的学习率η，对稀疏参数进行大幅更新和对频繁参数进行小幅更新。因此，Adagrad方法非常适合处理稀疏数据。

下面就是如何实现的

下面的r是我们给每个参数都要有的一个变量，初始为0，我们对一个参数来说，每次的参数更新都

要把梯度按平方和累加到该变量，假设该变量为S，梯度为g，t表示时间步，就是参数更新的第几次。

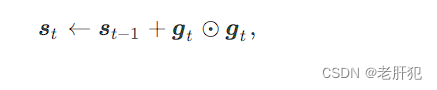
其中⊙ 是按元素相乘。接着，我们将目标函数自变量中每个元素的学习率通过按元素运算重新调整一下：

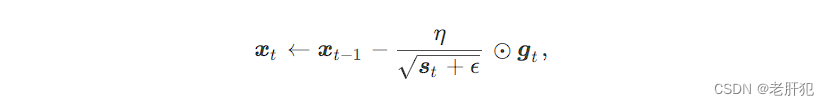
就和我们下面做的笔记一样。

优缺点

Adagrad方法的主要好处是，不需要手工来调整学习率。大多数参数使用了默认值0.01，且保持不变。

Adagrad方法的主要缺点是，学习率η总是在降低和衰减。

因为每个附加项都是正的，在分母中累积了多个平方梯度值，故累积的总和在训练期间保持增长。这反过来又导致学习率下降，变为很小数量级的数字，该模型完全停止学习，停止获取新的额外知识。

因为随着学习速度的越来越小，模型的学习能力迅速降低，而且收敛速度非常慢，需要很长的训练和学习，即学习速度降低。

RMSprop

原理

RMSProp算法是AdaGrad算法的改进，修改AdaGrad以在非凸条件下效果更好，解决了AdaGrad所面临的问题。

RMSProp主要思想：使用指数加权移动平均的方法计算累积梯度，以丢弃遥远的梯度历史信息（让距离当前越远的梯度的缩减学习率的权重越小）。

其他大致和上一个方法一样，就是多了一个不断减小的衰减系数。

牛顿法（Newton's Method）和拟牛顿法（Quasi-Newton Methods）

原理

（截图内容来自网络，侵权必删）

可以看一下这位网友在知乎的博客：理解牛顿法 - 知乎 (zhihu.com)

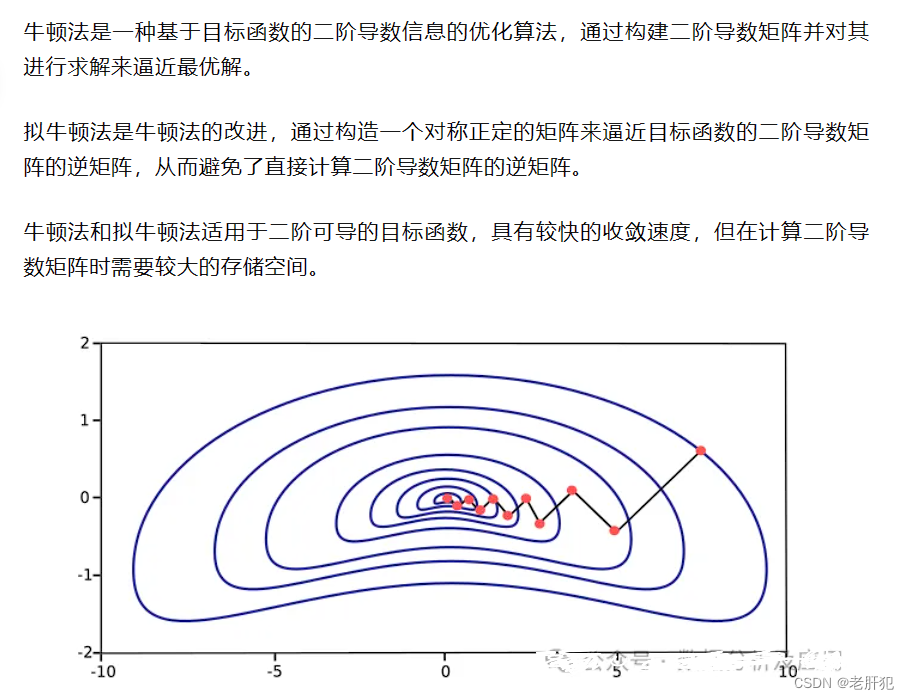
代码


import numpy as np  
from scipy.linalg import inv  
  
# 定义损失函数和Hessian矩阵  
def loss_function(w, X, y):  
    return np.sum(np.square(X.dot(w) - y)) / len(y)  
  
def hessian(w, X, y):  
    return X.T.dot(X) / len(y)  
  
# 定义牛顿法优化器  
def newton(X, y, learning_rate=0.01, epochs=100):  
    n_features = X.shape[1]  
    w = np.zeros(n_features)  
    for epoch in range(epochs):  
        H = hessian(w, X, y)  
        w -= inv(H).dot(gradient(w, X, y))  
        print("Epoch %d loss: %f" % (epoch+1, loss_function(w, X, y)))  
    return w

共轭梯度法（Conjugate Gradient）

共轭梯度法是介于梯度下降法和牛顿法之间的一种方法，利用共轭方向进行搜索。

共轭梯度法的优点是在每一步迭代中不需要计算完整的梯度向量，而是通过迭代的方式逐步逼近最优解。

该方法适用于大规模问题，尤其是稀疏矩阵和对称正定的问题。

LBFGS（Limited-memory Broyden–Fletcher–Goldfarb–Shanno）

原理

一种有限内存的Broyden-Fletcher-Goldfarb-Shanno（BFGS）算法，主要用于解决大规模优化问题。由于它只需要有限数量的计算机内存，因此特别适合处理大规模问题。LBFGS算法的目标是最小化一个给定的函数，通常用于机器学习中的参数估计。

代码


import numpy as np  
from scipy.optimize import minimize  
  
# 目标函数  
def objective_function(x):  
    return x**2 - 4*x + 4  
  
# L-BFGS算法求解最小值  
result = minimize(objective_function, x0=1, method='L-BFGS-B')  
x_min = result.x  
print(f"L-BFGS的最小值为：{objective_function(x_min)}")

SA（Simulated Annealing）

原理

一种随机搜索算法，其灵感来源于物理退火过程。该算法通过接受或拒绝解的移动来模拟退火过程，以避免陷入局部最优解并寻找全局最优解。在模拟退火算法中，接受概率通常基于解的移动的优劣和温度的降低，允许在搜索过程中暂时接受较差的解，这有助于跳出局部最优，从而有可能找到全局最优解。

代码


import numpy as np  
from scipy.optimize import anneal  
  
# 目标函数  
def objective_function(x):  
    return (x - 2)**2  
  
# SA算法求解最小值  
result = anneal(objective_function, x0=0, lower=-10, upper=10, maxiter=1000)  
x_min = result.x  
print(f"SA的最小值为：{objective_function(x_min)}")

AC-SA（Adaptive Clustering-based Simulated Annealing）

一种基于自适应聚类的模拟退火算法。通过模拟物理退火过程，利用聚类技术来组织解空间并控制解的移动。该方法适用于处理大规模、高维度的优化问题，尤其适用于那些具有多个局部最优解的问题。

遗传算法是一种基于自然选择和遗传学机理的生物进化过程的模拟算法，适用于解决优化问题，特别是组合优化问题。该算法通过数学的方式，利用计算机仿真运算，将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时，相对一些常规的优化算法，通常能够较快地获得较好的优化结果。