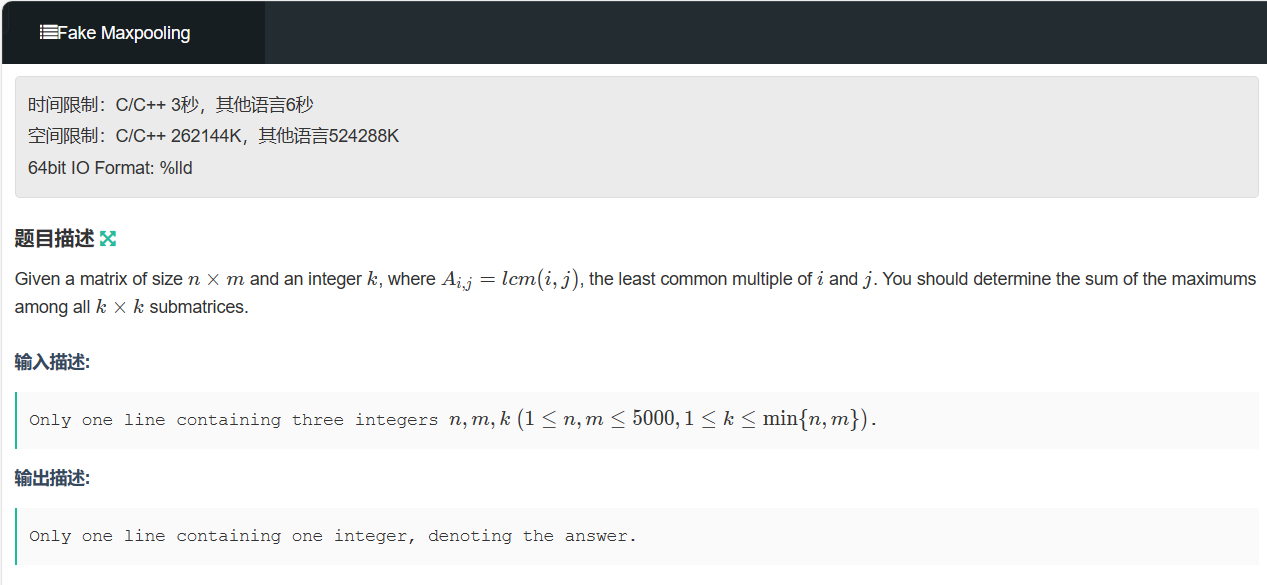
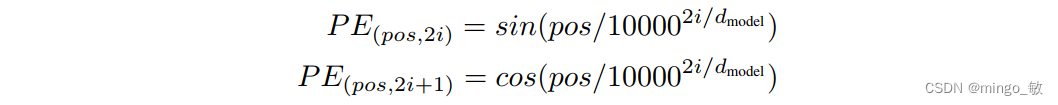矩阵乘法：

1、当矩阵A的列数（column）等于矩阵B的行数（row）时，A与B可以相乘。

Ankie的评论：一个人是站着的，一个人是躺着的，站着的高度=躺着的长度。

在计算attention的时候，因为QK是一样的矩阵，所以必须把K转置（躺下），才能相乘。

2、矩阵C的行数等于矩阵A的行数，C的列数等于B的列数。

3、乘积C的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。

Ankie的评论：C里面每个值，都是乘积之和（点积）。

矩阵乘法与点积dot product的关系：

因为点积是2个向量做运算：

两个向量a = [a1, a2,…, an]和b = [b1, b2,…, bn]的点积定义为：

a·b=a1b1+a2b2+……+anbn。

Ankie的评论：

跟上面矩阵乘法一对比，就看得出：

矩阵C的第一个元素，其实就是A的第一行和B的第一列做点积。

假如矩阵A只有一行，而B只有一列，矩阵乘法 == 向量点积。

假如矩阵A不止一行，而B也不止一行，矩阵乘法 ==  多个 向量点积。

这样就可以理解标题叫做dot-product attention，而实际上用的是矩阵乘法。

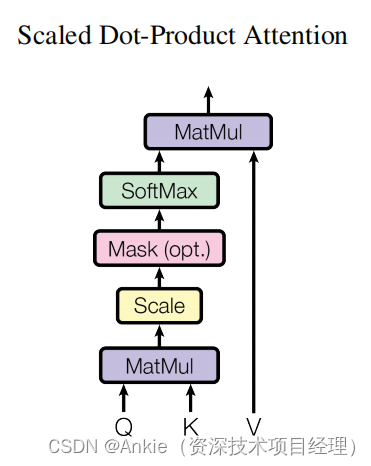
回到点积的几何作用：

Ankie的评论：因为点积可以计算相似值，或者距离，attention就拿来计算attention的相似值，或者距离。