二维双指针

思路:考虑暴力做法,我们统计前缀和,然后枚举以
(
x
1
,
y
1
)
(x_1,y_1)
(x1,y1),
(
x
2
,
y
2
)
(x_2,y_2)
(x2,y2)为左上,右下顶点的矩阵有多少是合法的,那么,这样的时间复杂度为
n
4
n^4
n4。考虑进行优化,因为二维前缀和同样具有单调性,我们可以选择枚举左,右边界,然后对于枚举的左右边界,使用双指针进行上下边界的计算,这样的时间复杂度就降低为了
n
3
n^3
n3。
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
typedef long long ll;
typedef pair<ll, ll> pll;
typedef array<int, 3> ar;
int mod = 1e9+7;
// const int maxv = 4e6 + 5;
// #define endl "\n"
int a[1005][1005];
int s[1005][1005];
void solve()
{
int n,m,k;
cin>>n>>m>>k;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>a[i][j];
s[i][j]=a[i][j]-s[i-1][j-1]+s[i][j-1]+s[i-1][j];
}
}
ll ans=0;
for(int i=1;i<=m;i++){
for(int j=i;j<=m;j++){
for(int c=1,t=1;c<=n;c++){
while(t<=c&&s[c][j]+s[t-1][i-1]-s[t-1][j]-s[c][i-1]>k) t++;
if(c>=t) ans+=c-t+1;
}
}
}
cout<<ans<<endl;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
t=1;
// cin>>t;
while(t--){
solve();
}
system("pause");
return 0;
}
二维滑动窗口
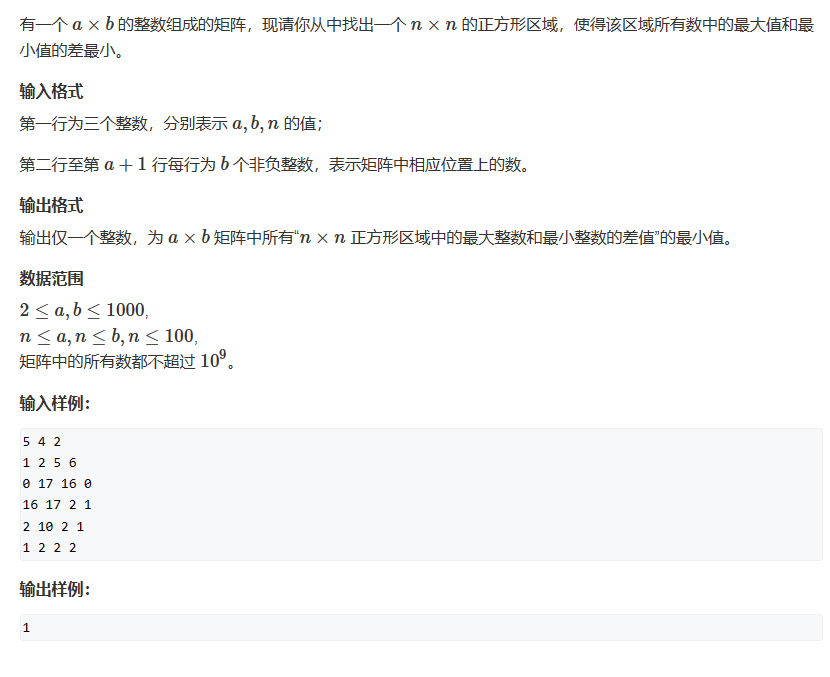
思路:首先考虑一维的情况,那么我们直接使用一个单调队列进行维护最大值和最小值即可,那么对于二维矩阵,以一个大小为
k
×
k
k\times k
k×k的矩阵为例,我们首先可以算出每一行中长度为k的最大值,此时我们知道了每一行的信息后,对于矩阵的最大值,肯定在前面已经算出来的行最大值中产生,我们再计算一遍列最大值即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5;
typedef long long ll;
typedef pair<ll, ll> pll;
typedef array<int, 3> ar;
int mod = 1e9+7;
// const int maxv = 4e6 + 5;
// #define endl "\n"
int n,m,k;
void solve()
{
cin>>n>>m>>k;
vector<vector<int>>a(n+5,vector<int> (m+5));
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++) cin>>a[i][j];
}
vector<vector<int>> rminv(n+5,vector<int> (m+5)),rmaxv(n+5,vector<int> (m+5));
//计算行最大值,rmaxv[i][j]代表第i行(j-k+1,j)内的最大值,rminv同理
auto getmax=[](vector<int> a,vector<int>& rmaxv,int m)//单调队列维护滑动窗口
{
deque<int> q;
for(int i=1;i<=m;i++){
if(q.size()&&i-q.front()+1>k) q.pop_front();
while(q.size()&&a[q.back()]<=a[i]) q.pop_back();
q.push_back(i);
rmaxv[i]=a[q.front()];
}
};
auto getmin=[](vector<int> a,vector<int>& rminv,int m)
{
deque<int> q;
for(int i=1;i<=m;i++){
if(q.size()&&i-q.front()+1>k) q.pop_front();
while(q.size()&&a[q.back()]>=a[i]) q.pop_back();
q.push_back(i);
rminv[i]=a[q.front()];
}
};
for(int i=1;i<=n;i++){
getmax(a[i],rmaxv[i],m);
getmin(a[i],rminv[i],m);
}
int ans=2e9;
vector<int> cmaxv(n+5),cminv(n+5),b(n+5),c(n+5);
//b,c数组用于保存n行的行最大值和最小值;cmaxv即为对n行的最大值进行计算,得出整个矩阵的最大值。
for(int i=k;i<=m;i++){
for(int j=1;j<=n;j++){
b[j]=rmaxv[j][i];
c[j]=rminv[j][i];
}
getmax(b,cmaxv,n);
getmin(c,cminv,n);
for(int i=k;i<=n;i++) ans=min(ans,cmaxv[i]-cminv[i]);
}
cout<<ans<<endl;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
t=1;
// cin>>t;
while(t--){
solve();
}
system("pause");
return 0;
}
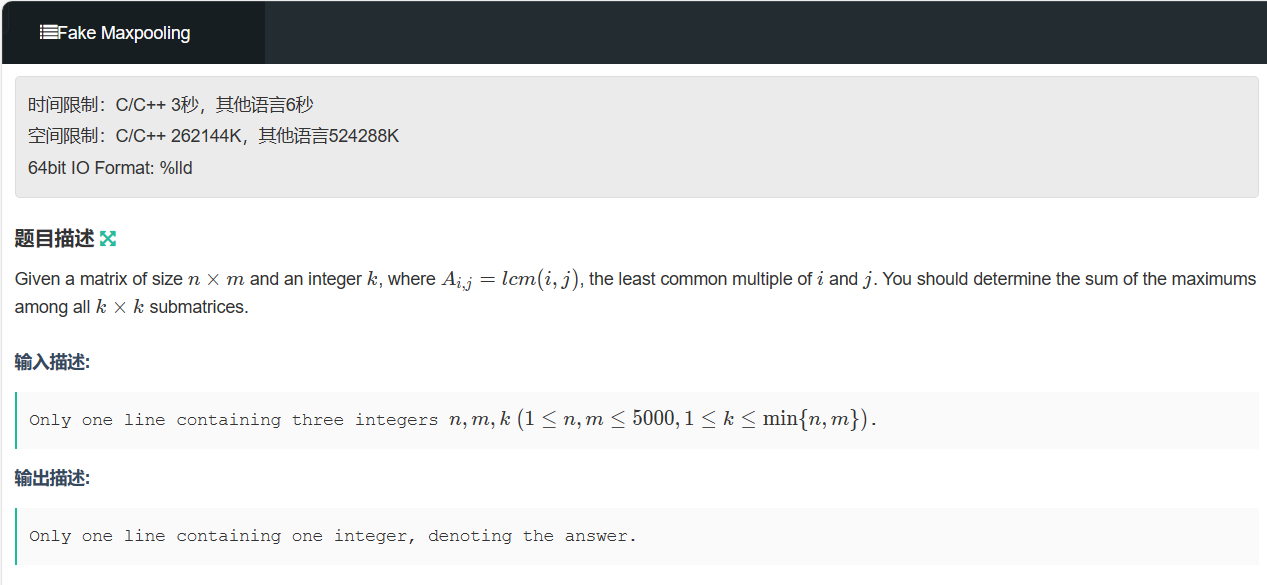
板子题,计算矩阵所有最大值的和即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 5e3 + 5;
typedef long long ll;
typedef pair<ll, ll> pll;
typedef array<int, 3> ar;
int mod = 1e9+7;
// const int maxv = 4e6 + 5;
// #define endl "\n"
int n,m,k;
void solve()
{
cin>>n>>m>>k;
vector<vector<int>> a (n+5,vector<int> (m+5));
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
a[i][j]=lcm(i,j);
}
}
vector<vector<int>>rmaxv(n+5,vector<int> (m+5));
auto getmax=[](vector<int> a,vector<int>& rmaxv,int m)
{
deque<int> q;
for(int i=1;i<=m;i++){
if(q.size()&&i-q.front()+1>k) q.pop_front();
while(q.size()&&a[q.back()]<=a[i]) q.pop_back();
q.push_back(i);
rmaxv[i]=a[q.front()];
}
};
for(int i=1;i<=n;i++){
getmax(a[i],rmaxv[i],m);
}
ll ans=0;
vector<int> cmaxv(n+5),b(n+5);
for(int i=k;i<=m;i++){
for(int j=1;j<=n;j++){
b[j]=rmaxv[j][i];
}
getmax(b,cmaxv,n);
for(int i=k;i<=n;i++) ans+=(ll)cmaxv[i];
}
cout<<ans<<endl;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
t=1;
// cin>>t;
while(t--){
solve();
}
system("pause");
return 0;
}