Hash 索引不支持顺序和范围查询;
二叉查找树(BST):解决了排序的问题,极端情况下可能会退化成线性链表,查询效率急剧下降;

平衡二叉树(AVL) :通过旋转解决了平衡的问题,但是旋转操作效率太低;
AVL 树是严格的平衡二叉树,所有节点的左右子树高度差不能超过 1

红黑树 :通过舍弃严格的平衡和引入红黑节点,解决了 AVL 旋转效率过低的问题,但是在磁盘等场景下,树仍然太高,IO 次数太多;
红黑树并不追求严格的平衡,而是大致的平衡:
节点是红色或黑色。
根是黑色。
所有叶子都是黑色(叶子是NIL节点)。
每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点(简称黑高)。红黑树保证最长路径不超过最短路径的二倍,因而近似平衡(最短路径就是全黑节点,最长路径就是一个红节点一个黑节点,当从根节点到叶子节点的路径上黑色节点相同时,最长路径刚好是最短路径的两倍)

B 树 :通过将二叉树改为多路平衡查找树,解决了树过高的问题;
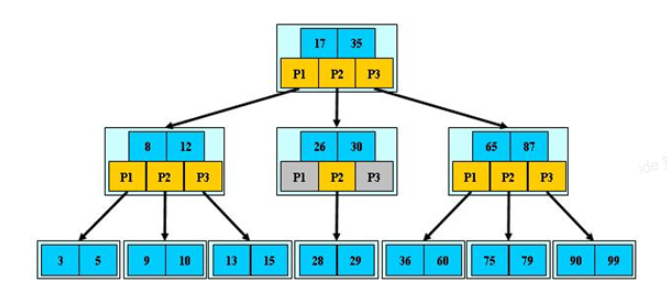
B+树 :B 树中每个节点(包括叶节点和非叶节点)都存储真实的数据,B+树中只有叶子节点存储真实的数据,非叶节点只存储键。因此能存更多记录。B+树的叶节点之间通过双向链表链接,因此更适合范围查询和排序查找。
InnoDB存储引擎中页的大小为16KB,一般表的主键类型为INT(占用4个字节)或BIGINT(占用8个字节),指针类型也一般为4或8个字节,也就是说一个页(B+Tree中的一个节点)中大概存储16KB/(8B+8B)=1K个键值(因为是估值,为方便计算,这里的K取值为〖10〗^3)。
也就是说一个深度为3的B+Tree索引可以维护10^3 * 10^3 * 10^3 = 10亿 条记录。(这种计算方式存在误差,而且没有计算叶子节点,如果计算叶子节点其实是深度为4了)
Mysql索引——B+树是怎么提高查询效率?_b+树的查询效率-CSDN博客