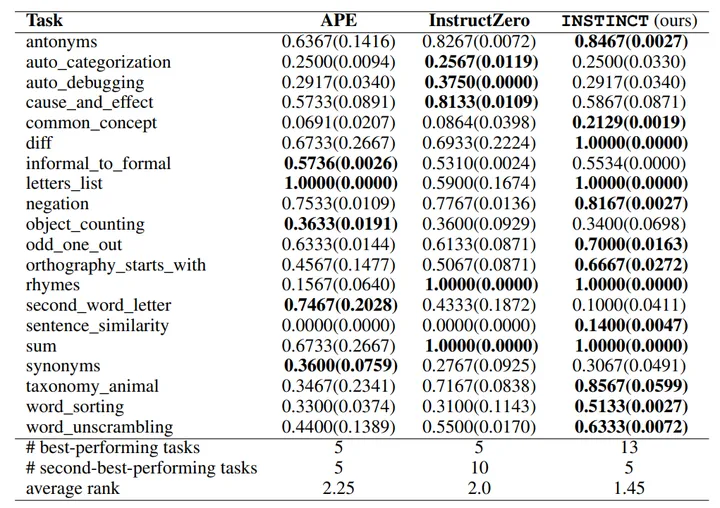
0网络稳定性 - 蓝桥云课 (lanqiao.cn)

知识点：克鲁斯卡尔生成树，lca，倍增

最小生成树的模板：最小生成树【模板】-CSDN博客

题解代码如下：

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+100;
const int inf=0x7fffffff;
int n,m,q;
struct point{
    int beg,end,dis;
};
point ed[N];
typedef pair<int,int> pii;
vector<pii>g[N];
bool vis[N];
int f[N];
int cost[N][20],dep[N],fa[N][20];
int find(int x)
{
    if(f[x]==x)
        return x;
    else
        return f[x]=find(f[x]);
}
void Union(int a,int b)
{
    a=find(a);
    b=find(b);
    if(a!=b)
        f[a]=b;
}
void krus()
{
    sort(ed,ed+m,[&](point a,point b){ return a.dis>b.dis; });   for(int i=0;i<m;i++)
    {
        if(find(ed[i].beg)!=find(ed[i].end))
        {
            Union(ed[i].beg,ed[i].end);
            g[ed[i].beg].push_back((pii){ed[i].end,ed[i].dis});
            g[ed[i].end].push_back((pii){ed[i].beg,ed[i].dis});
        }
    }
}

void dfs(int u,int fat)
{
    vis[u]=true;
    dep[u]=dep[fat]+1;//记录点的深度
    fa[u][0]=fat;//u点向上跳0^2次
    for(int i=1;i<=19;i++)
    {
        if(fa[u][i-1]>0)//递推点的所有能跳到的祖先节点
        {
            fa[u][i]=fa[fa[u][i-1]][i-1];
            cost[u][i]=min(cost[u][i-1],cost[fa[u][i-1]][i-1]);//存路径中的两相邻点间的路稳定性低那条路的值
        }
    }
    for(auto i:g[u])
    {
        if(i.first!=fat)
        {
            cost[i.first][0]=i.second;//到父节点的网络稳定性的值
            dfs(i.first,u);
        }
    }   
}
int lca(int u,int v)
{
    int res=inf;
    if(dep[u]<dep[v])//从u点找
        swap(u,v);
    int dx=dep[u]-dep[v];
    for(int i=0;dx>0;i++,dx=dx/2)//dx>>=1，让u,v到达树同一层
    {
        if(dx&1)
        {
            res=min(res,cost[u][i]);//保存路径中的两相邻节点间的路稳定性最低的那条路的值
            u=fa[u][i];
        }    
    }
    if(u==v)//特判，v点为u的祖先节点
        return res;
    for(int i=19;i>=0;i--)//让u，v点跳到公共祖先的儿子节点
    {
        if(fa[u][i]!=fa[v][i])
        {
            res=min(res,min(cost[u][i],cost[v][i]));//还是保存路径中的两相邻的点的网络稳定性低的那条路的值
            u=fa[u][i],v=fa[v][i];
        }
    }
    res=min(res,min(cost[u][0],cost[v][0]));//找到公共祖先后的:答案就是 u->公共祖先->v 的路径中每相邻两点的路的网络稳定性的最小值
    return res;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);cout.tie(nullptr);
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++)//初始化并查集
        f[i]=i;
    for(int i=0;i<m;i++)
    {
        cin>>ed[i].beg>>ed[i].end>>ed[i].dis;
    }
    krus();//生成最大树，因为找稳定性高的总路径
    for(int i=1;i<=n;i++)
    {
        if(!vis[i])//每个点以根节点遍历图，图可能不联通
            dfs(i,0);
    }
    while(q--)
    {
        int x,y;
        cin>>x>>y;
        if(find(x)==find(y))//查找两点是否可以到达
            cout<<lca(x,y)<<endl;
        else
            cout<<-1<<endl;
    }
    return 0;
}