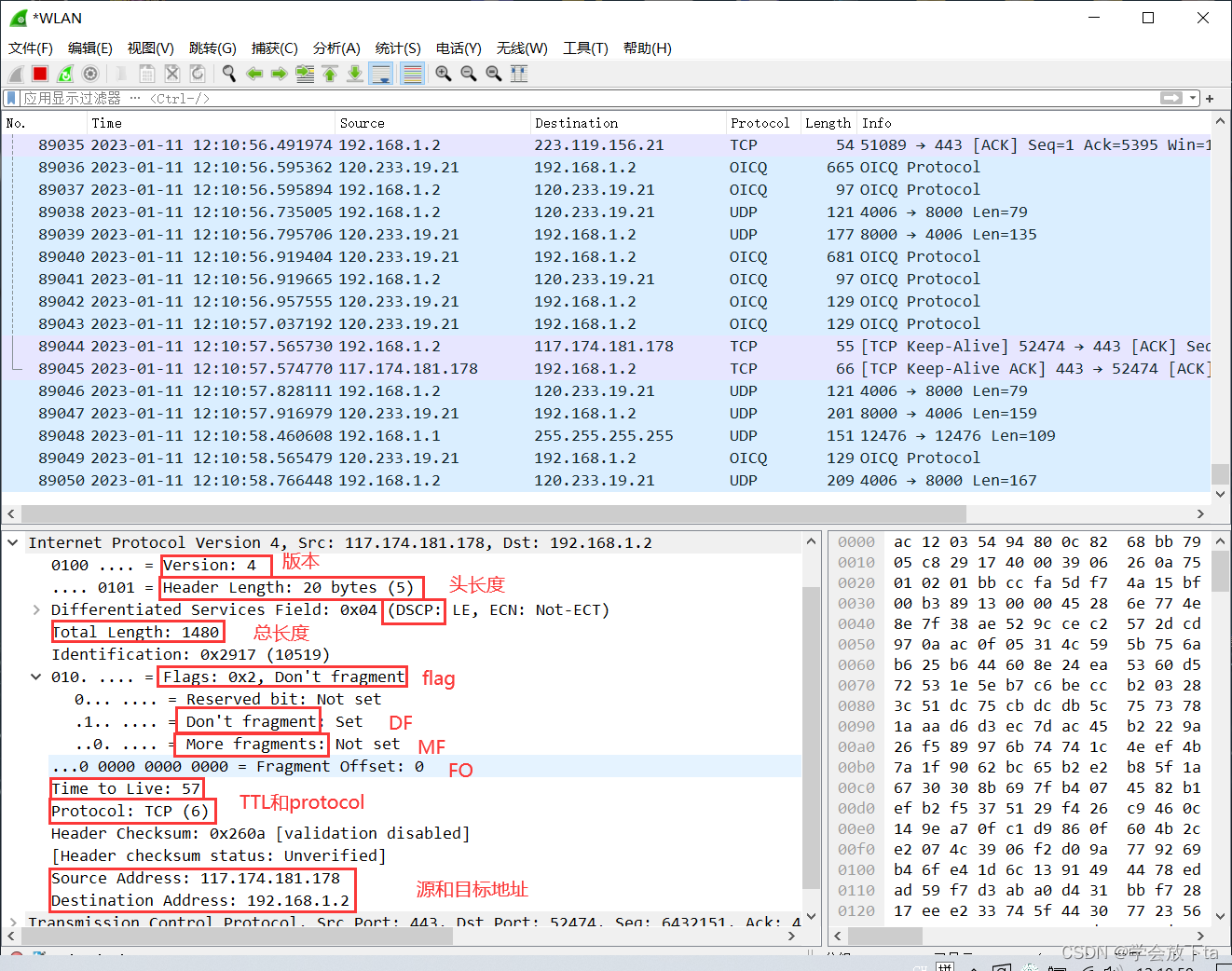
一、相关性模型(SPSS)
相关性模型涉及到两种最为常用的相关系数:
- 皮尔逊person相关系数
- 斯皮尔曼spearman等级相关系数
1、皮尔逊相关系数

相关性可视化


总结:
1.如果两个变量本身就是线性的关系,那么皮尔逊相关系数绝对值大的就是相关性强,小的就是相关性弱;
2.在不确定两个变量是什么关系的情况下,即使算出皮尔逊相关系数,发现很大,也不能说明那两个变量线性相关,甚至不能说他们相关,一定要先画出散点图来看才行。
2、斯皮尔曼相关系数

斯皮尔曼相关系数被定义成等级之间的皮尔逊相关系数
MATLAB中计算斯皮尔曼相关系数

代码:
% 必须为列向量,'表示求转置
X = [3 8 4 7 2]'
Y = [5 10 9 10 6]'
coeff = corr(X , Y , 'type' , 'Spearman')
二、回归模型
回归分析是数据分析中最基础也是最重要的分析工具,绝大多数的数据分析问题,都可以使用回归的思想来解决。回归分析的任务就是,通过研究自变量X和因变量Y的相关关系,尝试去解释Y的形成机制,进而达到通过X去预测Y的目的。
1、常见的回归分析:
- 线性回归(GDP增长率)
- 0-1回归(0表示还款/1表示未还款)
- 定序回归(1-5喜欢程度逐步增加)
- 计数回归(次数:非负)
- 生存回归(截断数据)
2、回归分析的分类

3、不同数据类型的处理方法

4、内生性的探究

5、内生性的蒙特卡罗模拟

代码:
%% 蒙特卡洛模拟:内生性会造成回归系数的巨大误差
% 蒙特卡洛的次数
times = 300;
R = zeros(times,1);
K = zeros(times,1);
for i = 1: times
n = 30;
x1 = -10+rand(n,1)*20;
u1 = normrnd(0,5,n,1) - rand(n,1);
x2 = 0.3*x1 + u1;
u = normrnd(0,1,n,1);
y = 0.5 + 2 * x1 + 5 * x2 + u ;
k = (n*sum(x1.*y)-sum(x1)*sum(y))/(n*sum(x1.*x1)-sum(x1)*sum(x1));
K(i) = k;
u = 5 * x2 + u;
r = corrcoef(x1,u);
R(i) = r(2,1);
end
plot(R,K,'*')
xlabel('x_1和u的相关系数')
ylabel('k的估计值')

三、多元线性回归分析
例1 多元线性回归
clear;
clc;
%多元线性回归
x1 = [7 1 11 11 7 11 3 1 2 21 1 11 10];
x2 = [26 29 56 31 52 55 71 31 54 47 40 66 68];
x3 = [6 15 8 8 6 9 17 31 54 47 40 66 68];
x4 = [60 52 20 47 33 22 6 44 22 26 34 12 12];
y = [78.5 74.3 104.3 87.6 95.9 109.2 102.7 72.5 93.1 115.9 83.8 113.3 109.4];
X = [ones(length(y), 1),x1',x2',x3',x4']
Y = y'
[b,bint,r,rint,stats] = regress(Y,X);
b,bint,stats
%残差图
figure(1);
rcoplot(r,rint)
%拟合图
figure(2);
z=b(1)+b(2)*x1+b(3)*x2+b(4)*x3+b(5)*x4;
plot(X,y,'k+',X,z)



残差图:

拟合图:

例2 成年女子的身高与腿长关系


%16名成年女子的身高与腿长所得数据
clear;
clc;
x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]';
y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]';
%配成y=a+b*x形式
plot(x,y,'r+')
%figure(1)
z=x;
x=[ones(16,1),x];
[b,bint,r,rint,stats]=regress(y,x);
%结果与polyfit(x,y,1)相同
b,bint,stats
rcoplot(r,rint)
plot(x,y,'r+')
hold on
a=140:165;
b=b(1)+b(2)*a;
%figure(3)
plot(140:165,b,'g')
残差分析,作残差图:

从残差图可以看出,除第二个数据外,其余数据的残差离零点均较近,且残差的置信区间均包含零点,这说明回归模型 y=-16.073+0.7194x能较好的符合原始数据,而第二个数据可视为异常点(而剔除)。
预测及作图:

例3 物体降落距离与时间关系

代码:直接作二次多项式回归
t=1/30:1/30:14/30;
s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];
[p,S]=polyfit(t,s,2)

s=489.2946t²+65.8896t+9.1329
四、多元非线性回归分析
使用格式:
beta = nlinfit(x,y, ‘ 程序名’,beta0)
[beta,r,J] = nlinfit(X,y,fun,beta0)
- X给定的自变量数据
- Y给定的因变量数据
- fun要拟合的函数模型(句柄函数或者内联函数形式)
- beta0函数模型中待定系数估计初值(即程序的初始实参)
- beta返回拟合后的待定系数其中beta为估计出的回归系数
- r为残差
- J为Jacobian矩阵
例1 混凝土抗压强度与时间

代码:
x=[2 3 4 5 7 9 12 14 17 21 28 56];
r=rand(1,12)-0.5;
y1=[35 42 47 53 59 65 68 73 76 82 86 99];
y=y1+r;
myfunc=inline('beta(1)+beta(2)*exp(beta(4)*x)+beta(3)*exp(-beta(4)*x)','beta','x');
beta=nlinfit(x,y,myfunc,[0.5 0.5 0.5 0.5]);
a=beta(1),k1=beta(2),k2=beta(3),m=beta(4)%test the model
xx=min(x):max(x);
yy=a+k1*exp(m*xx)+k2*exp(-m*xx);
plot(x,y,'o',xx,yy,'r')