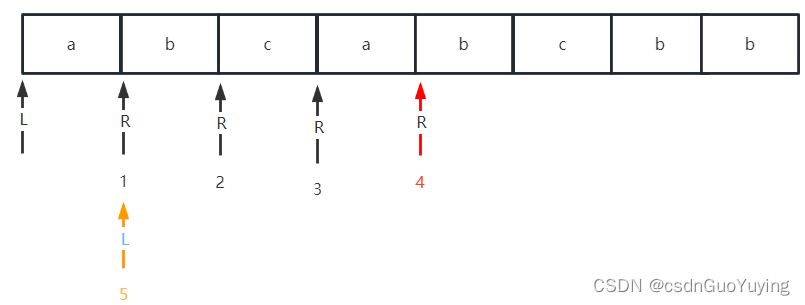
其实这题本身并不难,考的知识点就是归并排序和逆序对;
那么难点在哪呢?就在如何发现这题是个逆序对:
至少读到这里我们可以知道,虽然火柴高度是唯一的,但我们不可能直接开一个 max long int 大小的数组!很明显,有一个考点:离散化!
由此可见,若想使min(Σ[(ai-bi)^2])最小,而和式中ai^2+bi^2是个定值,那么,就只能在 2*aibi 这一项上
排列数。证明完成,那么我们要找的就是两个数列 l1, l2 中每一个数是否按我们所说的原则一一对应,比如说一个数列第1大的数对应另一个数列第1大的数,第2大的数对应另一个第2大的数,以此类推……
那么,不管三七二十一,先快排让两个序列有序一下吧(每个序列中火柴棒高度不同,不会导致编号混乱),反正有编号在那;然后我们来看一组数据(样例1)
A:2314->1234对应原编号为:3124
B:3214->1234对应原编号为:3214那么,A序列中输入的第一个数是第3小的,类推;
B序列中输入的第一个数是第3小的,符合,类推;
然我我们就发现了,A中第二个数与B中第二个数不一样(顺序不同),那么这就是一个逆序对,这个数不符合原则;不懂继续看看,等会就懂了;
找到不符合原则的数。
我们存一个数组c[i];
c[B[i]编号]=A[i]编号;为什么这么做?
数据说话:
A:2 3 1 4->1 2 3 4对应原编号为:3 1 2 4
B:3 2 1 4->1 2 3 4对应原编号为:3 2 1 4
c[B[1]编号]=c[3]=a[1]编号=3
c[B[2]编号]=c[2]=a[2]编号=1
c[B[3]编号]=c[1]=a[3]编号=2
c[B[4]编号]=c[4]=a[4]编号=4
于是c[1]=2 c[2]=1 c[3]=3 c[4]=4
逆序对数=1,交换一次,结束;神奇吗?不神奇,这就是排序;读到这里,读者应该对排序有了更深的理解;
为什么上述操作可以实现?因为产生了逆序;只要序列原来对应的数是符合要求的,他们编号相同,那么我们排完序两数的相对位置不发生改变,因此不会产生逆序;一旦A中编号与B中的不同,即大小顺序不同(顺序的整理快排都帮我们实现了),那么这个数是不符合要求的,我们需要处理一下,剩下的在c数组中的数都是符合要求的(也就就是计入逆序对)。想到这里,程序就over了;不信的读者可以把第二个样例按我上面的分析写出来,自己也可以再写几组简单的样例,多过几遍流程;

#include<cstdio>
#include<algorithm>
using namespace std;
const int mod=99999997;
long long n,x[10000005],p[1000005],ans=0;
struct fire{
int hi,bh;
}l1[1000005],l2[1000005];
bool cmp1(fire a,fire b)
{
return a.hi<b.hi;
}
void msort(int s,int t)//归并排序;
{
if(s==t)return ;
int mid=(s+t)/2;
msort(s,mid);msort(mid+1,t);
int i=s,k=s,j=mid+1;
while(i<=mid && j<=t)
{
if(x[i]<=x[j])
{
p[k]=x[i];
++k;++i;
}
else
{
p[k]=x[j];
++k;++j;
ans=(ans+mid-i+1)%mod;
//此处找到逆序对,mid-i~mid中数全都与j构成逆序,还会少算一个,+1;
}
}
while(i<=mid)
{
p[k]=x[i];
++k;++i;
}
while(j<=t)
{
p[k]=x[j];
++k;++j;
}
for(int i=s;i<=t;i++)
{
x[i]=p[i];
}
}
int main()
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)
scanf("%d",&l1[i].hi),l1[i].bh=i;
for(int i=1;i<=n;i++)
scanf("%d",&l2[i].hi),l2[i].bh=i;
sort(l1+1,l1+n+1,cmp1);
sort(l2+1,l2+n+1,cmp1);
//排序;
for(int i=1;i<=n;i++)
x[l2[i].bh]=l1[i].bh;
msort(1,n);
//调用归并;
printf("%lld",ans);
return 0;//这个不会有人忘的吧?
}over~加油加油,慢慢来