CCF-CSP认证考试 202212-3 JPEG 解码 100分题解

更多 CSP 认证考试题目题解可以前往：CSP-CCF 认证考试真题题解

原题链接： 202212-3 JPEG 解码

时间限制： 1.0s
内存限制： 512.0MB

问题背景

四年一度的世界杯即将画上尾声。在本次的世界杯比赛中，视频助理裁判（Video Assistant Referee, VAR）的应用可谓是大放异彩。VAR 使用视频回放技术帮助主裁判作出正确判罚决定。西西艾弗岛足球联赛的赛场上也引入了一套 VAR 设备。作为技术供应商的技术主管小C，需要存储和编码 VAR 产生的图像数据。小 C 分析比较发现，JPEG 编码算法可以达到较好的压缩效果，并且质量损失是可以接受的。因此，小 C 决定使用 JPEG 编码算法来存储和传输图像数据。JPEG 是一种常用的图片有损压缩算法，它的压缩率高，但是压缩后的图片质量下降较多。JPEG 图片的压缩率一般在 10:1 到 20:1 之间，一般用于存储照片等图片质量要求不高的场景。

为了简化问题，我们以灰度图片为例，介绍 JPEG 编码算法的过程。一张灰度图片，可以被视为由多个像素点组成。每个像素点对应一个 0 到 255 之间的数值，用于表示像素点的亮度。JPEG 编码算法将图片分割为 $\times 8$ 的小块，每个小块被称作一个最小编码单元。对每个小块进行如下的计算：

将每个像素点的数值减去 128，使得每个像素点的数值都在 -128 到 127 之间。
将每个小块的像素点排成一个 $\times 8$ 的矩阵，并对矩阵进行离散余弦变换（DCT）。进行离散余弦变换后，仍然得到一个 $\times 8$ 的矩阵，矩阵中的每个元素都是实数，并且所得矩阵的左上方的数字的绝对值较大，右下方的数字的绝对值较小，甚至接近 0。
对矩阵进行量化操作。量化操作是指将矩阵中的每个元素都除以一个数字，并取整数。量化操作的目的是为了减少矩阵中的数据，从而减少编码后的文件大小。量化操作的数字越大，矩阵中的数据就越少，但是压缩后的图片质量也会越差。
对矩阵进行 Z 字形扫描。Z 字形扫描是指从左上角开始，沿着 Z 字形的路径扫描矩阵中的元素，将扫描到的元素依次排成一个数组，由于 Z 字形扫描的路径是从左上角到右下角，数组结尾处可能存在着连续的 0，为了节省空间，可以不存储这些连续的 0。得到的数据被称为扫描数据。

最后，将得到的各个小块的扫描数据采用哈夫曼编码进行压缩，并置于必要的数据结构中，就能得到一张 JPEG 图片了。

问题描述

在本题中，你需要实现一个能够解码 JPEG 图片的一个最小编码单元的程序。解码的步骤与上述编码的步骤相反，具体的步骤是：

读入量化矩阵 $Q_{i,j}$ ，其中 $i, j$ 的取值范围为 $\sim 7$ 。
初始化一个 $\times 8$ 的矩阵 $M$ ，令 $M_{i,j} = 0$ 。
读入扫描数据，将扫描数据按照这样的顺序写入矩阵 $M$ ：从左上角 $M_{0,0}$ 开始，接下来填充它的右侧相邻的元素 $M_{0,1}$ ，然后依次向左下方填充直至 $M_{1,0}$ ，接下来从它下侧相邻的元素 $M_{2,0}$ 开始，依次向右上方填充直至 $M_{0, 2}$ ，依次类推，循环往复，直至填充满整个矩阵或用尽所有扫描数据，如图所示。

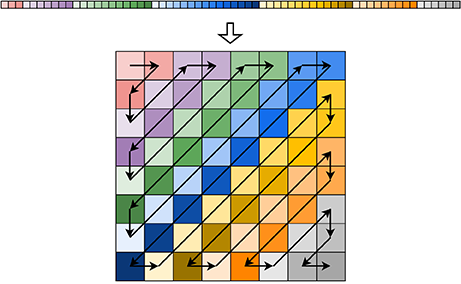
填充顺序
将矩阵 $M$ 中的每个元素都乘以量化矩阵 $Q$ 中的对应元素。
对矩阵 $M$ 进行离散余弦逆变换，得到一个 $\times 8$ 的矩阵 $M^{'}$ 。其中，逆变换的公式如下：
$M'_{i,j} = \frac{1}{4} \sum_{u=0}^{7} \sum_{v=0}^{7} \alpha(u) \alpha(v) M_{u,v} \cos \left( \frac{\pi}{8} \left( i + \frac{1}{2} \right) u \right) \cos \left( \frac{\pi}{8} \left( j + \frac{1}{2} \right) v \right)$ 其中 $\alpha(u) = \begin{cases} \sqrt{\frac{1}{2}} & u = 0 \\ 1 & u \neq 0 \end{cases}$
将矩阵 $M^{'}$ 中的每个元素都加上 $128$ ，并取最接近的整数（四舍五入）。如果得到的整数大于 $255$ ，则取 $255$ ；如果得到的整数小于 $0$ ，则取 $0$ 。得到的矩阵即为解码后的图片。

例如，假设给定的量化矩阵是：
$\begin{bmatrix} 16 & 11 & 10 & 16 & 24 & 40 & 51 & 61 \\ 12 & 12 & 14 & 19 & 26 & 58 & 60 & 55 \\ 14 & 13 & 16 & 24 & 40 & 57 & 69 & 56 \\ 14 & 17 & 22 & 29 & 51 & 87 & 80 & 62 \\ 18 & 22 & 37 & 56 & 68 & 109 & 103 & 77 \\ 24 & 35 & 55 & 64 & 81 & 104 & 113 & 92 \\ 49 & 64 & 78 & 87 & 103 & 121 & 120 & 101 \\ 72 & 92 & 95 & 98 & 112 & 100 & 103 & 99 \\ \end{bmatrix}$

给出的扫描数据是：-26, -3, 0, -3, -2, -6, 2, -4, 1, -3, 1, 1, 5, 1, 2, -1, 1, -1, 2, 0, 0, 0, 0, 0, -1 -1，那么填充后的矩阵 $M$ 是：
$\begin{bmatrix} -26 & -3 & -6 & 2 & 2 & -1 & 0 & 0 \\ 0 & -2 & -4 & 1 & 1 & 0 & 0 & 0 \\ -3 & 1 & 5 & -1 & -1 & 0 & 0 & 0 \\ -3 & 1 & 2 & -1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix}$

与量化矩阵逐项相乘后的矩阵是：
$\begin{bmatrix} -416 & -33 & -60 & 32 & 48 & -40 & 0 & 0 \\ 0 & -24 & -56 & 19 & 26 & 0 & 0 & 0 \\ -42 & 13 & 80 & -24 & -40 & 0 & 0 & 0 \\ -42 & 17 & 44 & -29 & 0 & 0 & 0 & 0 \\ 18 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{bmatrix}$

经过离散余弦逆变换后的矩阵 $M^{'}$ 是：
$\begin{bmatrix} -65.83 & -62.63 & -71.04 & -68.04 & -55.65 & -64.99 & -68.37 & -45.72 \\ -70.87 & -72.59 & -72.07 & -45.82 & -20.30 & -40.63 & -65.74 & -57.11 \\ -70.40 & -78.12 & -68.13 & -17.40 & 19.72 & -14.45 & -60.84 & -63.38 \\ -63.00 & -73.21 & -61.78 & -7.56 & 26.97 & -13.59 & -60.21 & -57.75 \\ -58.02 & -65.09 & -61.36 & -27.06 & -6.29 & -40.45 & -67.70 & -50.14 \\ -57.26 & -57.09 & -64.34 & -57.62 & -48.02 & -65.58 & -72.36 & -47.25 \\ -53.45 & -45.52 & -60.89 & -73.60 & -64.55 & -63.43 & -62.21 & -44.67 \\ -47.14 & -34.38 & -53.26 & -73.78 & -60.19 & -47.06 & -46.88 & -40.80 \\ \end{bmatrix}$

经过加 $128$ 后并取整的矩阵是：
$\begin{bmatrix} 62 & 65 & 57 & 60 & 72 & 63 & 60 & 82 \\ 57 & 55 & 56 & 82 & 108 & 87 & 62 & 71 \\ 58 & 50 & 60 & 111 & 148 & 114 & 67 & 65 \\ 65 & 55 & 66 & 120 & 155 & 114 & 68 & 70 \\ 70 & 63 & 67 & 101 & 122 & 88 & 60 & 78 \\ 71 & 71 & 64 & 70 & 80 & 62 & 56 & 81 \\ 75 & 82 & 67 & 54 & 63 & 65 & 66 & 83 \\ 81 & 94 & 75 & 54 & 68 & 81 & 81 & 87 \\ \end{bmatrix}$

输入格式

从标准输入读入数据。

输入的前 8 行，每行有空格分隔 8 个正整数，是量化矩阵。

接下来的 1 行是 1 个正整数 $n$ ，表示扫描数据的个数。

接下来的 1 行是 1 个数字 $T$ ，取值为 0、1 或 2，表示要进行的任务。

接下来的 1 行，有空格分隔的 $n$ 个整数，是扫描数据。

输出格式

输出到标准输出中。

输出共 8 行，每行有 8 个空格分隔的整数，表示一个图像矩阵。

当 $T$ 取 0 时，输出填充（步骤 3）后的图像矩阵；当 $T$ 取 1 时，输出量化（步骤 4）后的图像矩阵；当 $T$ 取 2 时，输出最终的解码结果。

样例输入

16 11 10 16 24 40 51 61
12 12 14 19 26 58 60 55
14 13 16 24 40 57 69 56
14 17 22 29 51 87 80 62
18 22 37 56 68 109 103 77
24 35 55 64 81 104 113 92
49 64 78 87 103 121 120 101
72 92 95 98 112 100 103 99
26
2
-26 -3 0 -3 -2 -6 2 -4 1 -3 1 1 5 1 2 -1 1 -1 2 0 0 0 0 0 -1 -1

样例输出

62 65 57 60 72 63 60 82
57 55 56 82 108 87 62 71
58 50 60 111 148 114 67 65
65 55 66 120 155 114 68 70
70 63 67 101 122 88 60 78
71 71 64 70 80 62 56 81
75 82 67 54 63 65 66 83
81 94 75 54 68 81 81 87

样例说明

本组样例即为题目描述中的样例。

子任务

对于 20% 的数据，有 $T = 0$ ；

对于 40% 的数据，有 $T = 0$ 或 $1$ ；

对于 100% 的数据，有 $\in \left\{0, 1, 2\right\}$ ，且 $\in \left[0, 64\right]$ ，并且量化矩阵中的各个元素 $q_{i,j}$ 满足 $0 < q_{i,j} < 256$ ，扫描序列中的各个元素 $m_i$ 满足 $256 < m_i < 256$ 。

提示

在 C/C++ 语言中，可以通过包含 math.h（C 语言）或 cmath（C++ 语言）来使用数学函数。 $\pi$ 的值可以通过表达式 acos(-1) 获得。

在 Python 语言中，可以通过 from math import pi 引入 $\pi$ 。

在 Java 语言中，可以使用 Math.PI 来获取 $\pi$ 的值.

题解

构造矩阵 $M$ 的时候设置一个变量 $d i r$ 表示方向， $d i r = 0$ 时从左下往右上填充， $d i r = 1$ 时从右上往左下填充。注意判断边界是两个维度都要考虑是否到达边界。

别的直接根据题目的信息和公式操作即可，别忘了在输出前要把范围更改到 $[0, 255]$ 中，并四舍五入到整数。

时间复杂度： $\mathcal{O}(8^4)$ 。

参考代码（0ms，2.917MB）

/*
    Created by Pujx on 2024/3/25.
*/
#pragma GCC optimize(2, 3, "Ofast", "inline")
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
//#define int long long
//#define double long double
using i64 = long long;
using ui64 = unsigned long long;
using i128 = __int128;
#define inf (int)0x3f3f3f3f3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define yn(x) cout << (x ? "yes" : "no") << endl
#define Yn(x) cout << (x ? "Yes" : "No") << endl
#define YN(x) cout << (x ? "YES" : "NO") << endl
#define mem(x, i) memset(x, i, sizeof(x))
#define cinarr(a, n) for (int i = 1; i <= n; i++) cin >> a[i]
#define cinstl(a) for (auto& x : a) cin >> x;
#define coutarr(a, n) for (int i = 1; i <= n; i++) cout << a[i] << " \n"[i == n]
#define coutstl(a) for (const auto& x : a) cout << x << ' '; cout << endl
#define all(x) (x).begin(), (x).end()
#define md(x) (((x) % mod + mod) % mod)
#define ls (s << 1)
#define rs (s << 1 | 1)
#define ft first
#define se second
#define pii pair<int, int>
#ifdef DEBUG
    #include "debug.h"
#else
    #define dbg(...) void(0)
#endif

const int N = 2e5 + 5;
//const int M = 1e5 + 5;
const int mod = 998244353;
//const int mod = 1e9 + 7;
//template <typename T> T ksm(T a, i64 b) { T ans = 1; for (; b; a = 1ll * a * a, b >>= 1) if (b & 1) ans = 1ll * ans * a; return ans; }
//template <typename T> T ksm(T a, i64 b, T m = mod) { T ans = 1; for (; b; a = 1ll * a * a % m, b >>= 1) if (b & 1) ans = 1ll * ans * a % m; return ans; }

int a[N];
int n, m, t, k, q;
const double val = sqrt(0.5);
const double pi = acos(-1);

template <typename T = int> struct Matrix {
    int m, n; // m 行 n 列的矩阵
    vector<vector<T>> v;

    Matrix(): n(0), m(0) { v.resize(0); }
    Matrix(int r, int c, T num = T()) : m(r), n(c) {
        v.resize(m, vector<T>(n, num));
    }
    Matrix(int n) : m(n), n(n) { // 单位矩阵的构造函数
        v.resize(n, vector<T>(n, 0));
        for (int i = 0; i < n; i++) v[i][i] = 1;
    }

    Matrix& operator += (const Matrix& b) & {
        assert(m == b.m && n == b.n);
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                v[i][j] += b[i][j];
        return *this;
    }
    Matrix& operator -= (const Matrix& b) & {
        assert(m == b.m && n == b.n);
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                v[i][j] -= b[i][j];
        return *this;
    }
    Matrix& operator *= (const T& b) & {
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                v[i][j] *= b;
        return *this;
    }
    Matrix& operator *= (const Matrix& b) & {
        assert(n == b.m);
        Matrix ans(m, b.n);
        for (int i = 0; i < m; i++)
            for (int j = 0; j < b.n; j++)
                for (int k = 0; k < n; k++)
                    ans[i][j] += v[i][k] * b[k][j];
        return *this = ans;
    }
    friend Matrix operator + (const Matrix& a, const Matrix& b) {
        Matrix ans = a; ans += b; return ans;
    }
    friend Matrix operator - (const Matrix& a, const Matrix& b) {
        Matrix ans = a; ans -= b; return ans;
    }
    friend Matrix operator * (const Matrix& a, const T& b) {
        Matrix ans = a; a *= b; return ans;
    }
    friend Matrix operator * (const Matrix& a, const Matrix& b) {
        Matrix ans = a; ans *= b; return ans;
    }
    Matrix trans() const {
        Matrix ans(n, m);
        for (int i = 0; i < n; i++)
            for (int j = 0; j < m; j++)
                ans[i][j] = v[j][i];
        return ans;
    }
    Matrix ksm(const long long& x) const {
        assert(n == m);
        Matrix ans(n), a = *this;
        for (long long pw = x; pw; a *= a, pw >>= 1) if (pw & 1) ans *= a;
        return ans;
    }
    vector<T>& operator [] (const int& t) { return v[t]; }
    const vector<T>& operator [] (const int& t) const { return v[t]; }

    friend bool operator == (const Matrix& a, const Matrix& b) {
        assert(a.m == b.m && a.n == b.n);
        for (int i = 0; i < a.m; i++)
            for (int j = 0; j < a.n; j++)
                if (a[i][j] != b[i][j])
                    return false;
        return true;
    }
    friend bool operator != (const Matrix& a, const Matrix& b) {
        return !(a == b);
    }

    friend istream& operator >> (istream& in, Matrix& x) {
        for (int i = 0; i < x.m; i++)
            for (int j = 0; j < x.n; j++)
                in >> x[i][j];
        return in;
    }
    friend ostream& operator << (ostream& out, const Matrix& x) {
        for (int i = 0; i < x.m; i++)
            for (int j = 0; j < x.n; j++)
                out << x[i][j] << " \n"[j == x.n - 1];
        return out;
    }
};

void work() {
    Matrix<int> Q(8, 8), M(8, 8);
    cin >> Q >> n >> t;
    cinarr(a, n);

    bool dir = false;
    int x = 0, y = 0;
    for (int i = 1; i <= n; i++) {
        M[x][y] = a[i];
        if (!dir && (!x || y == 7)) dir = true, y == 7 ? x++ : y++;
        else if (!dir) x--, y++;
        else if (!y || x == 7) dir = false, x == 7 ? y++ : x++;
        else x++, y--;
    }
    if (t == 0) return cout << M, void();

    for (int i = 0; i < 8; i++)
        for (int j = 0; j < 8; j++)
            M[i][j] *= Q[i][j];
    if (t == 1) return cout << M, void();

    auto alpha = [&] (int u) -> double {
        if (!u) return val;
        else return 1;
    };
    Matrix<double> M1(8, 8);
    for (int i = 0; i < 8; i++)
        for (int j = 0; j < 8; j++) {
            for (int u = 0; u < 8; u++)
                for (int v = 0; v < 8; v++)
                    M1[i][j] += alpha(u) * alpha(v) * M[u][v] * cos(pi / 8 * (i + 0.5) * u) * cos(pi / 8 * (j + 0.5) * v);
            M1[i][j] /= 4;
            M1[i][j] += 128;
            M1[i][j] = max(M1[i][j], 0.0);
            M1[i][j] = min(M1[i][j], 255.0);
        }
    cout << fixed << setprecision(0) << M1;
}

signed main() {
#ifdef LOCAL
    freopen("C:\\Users\\admin\\CLionProjects\\Practice\\data.in", "r", stdin);
    freopen("C:\\Users\\admin\\CLionProjects\\Practice\\data.out", "w", stdout);
#endif
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    int Case = 1;
    //cin >> Case;
    while (Case--) work();
    return 0;
}
/*
     _____   _   _       _  __    __
    |  _  \ | | | |     | | \ \  / /
    | |_| | | | | |     | |  \ \/ /
    |  ___/ | | | |  _  | |   }  {
    | |     | |_| | | |_| |  / /\ \
    |_|     \_____/ \_____/ /_/  \_\
*/

关于代码的亿点点说明：

代码的主体部分位于 void work() 函数中，另外会有部分变量申明、结构体定义、函数定义在上方。
#pragma ... 是用来开启 O2、O3 等优化加快代码速度。
中间一大堆 #define ... 是我习惯上的一些宏定义，用来加快代码编写的速度。
"debug.h" 头文件是我用于调试输出的代码，没有这个头文件也可以正常运行（前提是没定义 DEBUG 宏），在程序中如果看到 dbg(...) 是我中途调试的输出的语句，可能没删干净，但是没有提交上去没有任何影响。
ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); 这三句话是用于解除流同步，加快输入 cin 输出 cout 速度（这个输入输出流的速度很慢）。在小数据量无所谓，但是在比较大的读入时建议加这句话，避免读入输出超时。如果记不下来可以换用 scanf 和 printf，但使用了这句话后，cin 和 scanf、cout 和 printf 不能混用。
将 main 函数和 work 函数分开写纯属个人习惯，主要是为了多组数据。