人工智能的决策树介绍

news2024/9/30 23:31:51

决策树模型

决策树基于“树”结构进行决策

每个“内部结点”对应于某个属性上的“测试”
每个分支节点对应于该测试的一种可能结果（即属性的某个取值）
每个“叶结点”对应于一个“预测结果”

学习过程：通过对训练样本的分析来确定“划分属性”（即内部结点所对应的属性）

预测过程：将测试示例从根结点开始，沿着划分属性所构成的“判定测试序列”下行，直到叶结点

决策树简史

第一个决策树算法：CLS（Concept Learning System）

使决策树受到关注、成为机器学习主流技术的算法：ID3

最常用的决策树算法：C4.5

可以用于回归任务的决策树算法：CART(Classification and Regression Tree)

基于决策树的最强大算法：RF(Random Forest)

决策树的基本算法

基本流程：

策略：“分而治之”

自根至叶的递归过程

在每个中间结点寻找一个“划分”属性

三种停止条件：①当前结点包含的样本全属于同一类别，无需划分；②当前属性集为空，或是所有样本在属性集上取值相同，无法划分；③当前结点包含的样本集合为空，不能划分

信息增益

信息熵

信息熵是度量样本集合“纯度”最常用的一种指标

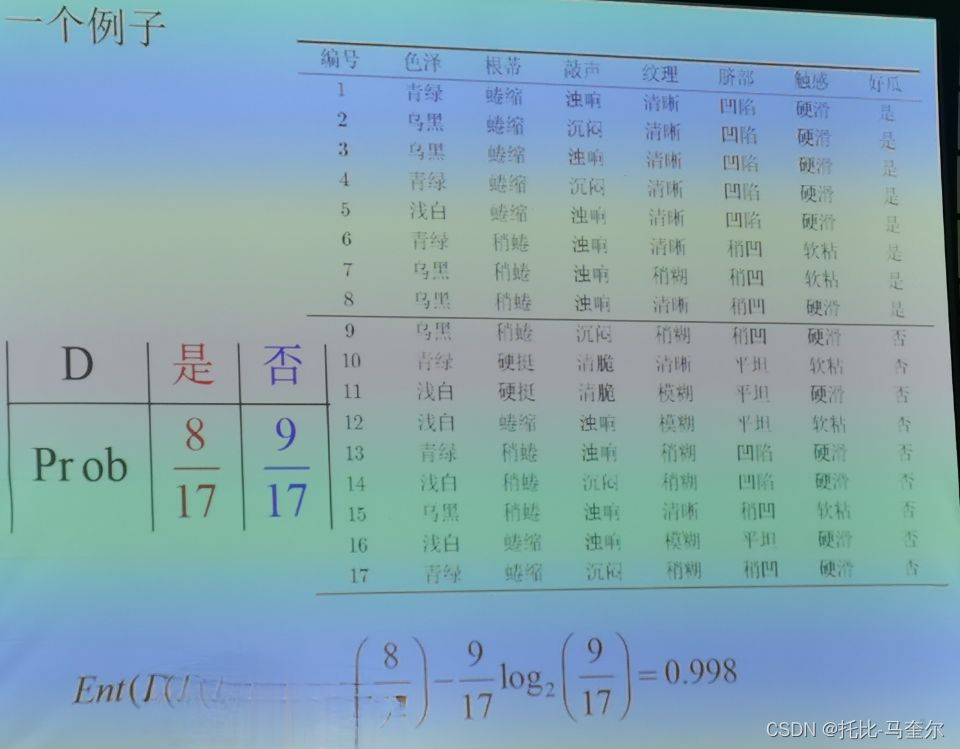
假设当前样本集合D中第k类样本所占的比例为 $p_{k}$ ,则D的信息熵定义为：

$Ent(D)=-\sum_{k=1}^{|y|}p_{k}log_{2}(p_{k})$

其中y指的是总共有多少个类

Ent(D)的值越小，则D的纯度越高

如果p=0,则 $plog_{2}(p)=0$

Ent(D)的最小值：0，此时D只有一类；

最大值： $log_{2}(y)$ ，此时D每个样本都是一类

信息增益

离散属性a的取值：{ $a^1,a^2...a^v$ }

$D_{v}$ ：D中在a上取值= $a^v$ 的样本集合

以属性a对数据集D进行划分所获得的信息增益为：

$Gain(D,a) = Ent(D)-\sum_{v=1}^{V}\frac{|D^v|}{|D|}Ent(D^v)$

信息增益指的是划分前的信息熵--划分后的信息熵

$\frac{|D^v|}{|D|}$ 指的是第v个分支的权重，样本越多越重要

生成决策树的例子

增益率

信息增益：对可取值数目较多的属性有所偏好

$Gain_-ratio(D,a)=\frac{Gain(D,a)}{IV(a)}$

其中 $IV(a)= -\sum_{v=1}^{V}\frac{|D^v|}{|D|}log_{2}\frac{|D^v|}{|D|}$

属性a的可能取值数目（即分支V越多），则 $IV(a)$ 的值通常就越大

启发式：先从候选划分属性中找出信息增益高于平均水平的，再从中选取增益率最高的

基尼指数

$Gini(D)=\sum_{k=1}^{|y|}\sum_{k'!=k}{p_{k}p_{k'}}=1-\sum_{k=1}^{|y|}p_{k}^{2}$

基尼指数越小，数据集D的纯度就越高

属性a的基尼指数： $Gini_-index(D,a)=\sum_{v=1}^{V}\frac{|D^{v}|}{|D|}Gini(D^{v})$

在侯选属性集合中，选取那个使划分后基尼指数最小的属性

划分选择vs剪枝

划分选择的各种准则虽然对决策树的尺寸有较大影响，但对泛化性能的影响很有限

剪枝方法和程度对决策树泛化性能的影响更为显著

剪枝是决策树对付“过拟合”的主要手段

剪枝

为了尽可能正确分类训练样本，有可能造成分支过多->过拟合，可通过主动去掉一些分支来降低过拟合的风险

预剪枝

提前终止某些分支的生长

后剪枝

生成一棵完全树，再“回头”剪枝

	预剪枝	后剪枝
时间开销	训练时间开销降低，测试时间开销降低	训练时间开销增加，测试时间开销降低
过/欠拟合风险	过拟合风险降低，欠拟合风险增加	过拟合风险降低，欠拟合风险基本不变
泛化性能	后剪枝通常优于预剪枝

连续值

基本思路：连续属性离散化

连续变量 $x_{1}<x_{2}<....<x_{n}$ ，取区间的中点 $\frac{x_{i}+x_{i+1}}{2}$ 作为属性值

常见做法：二分法

n个属性值可形成n-1个候选划分

然后可将它们当做n-1个离散属性值处理

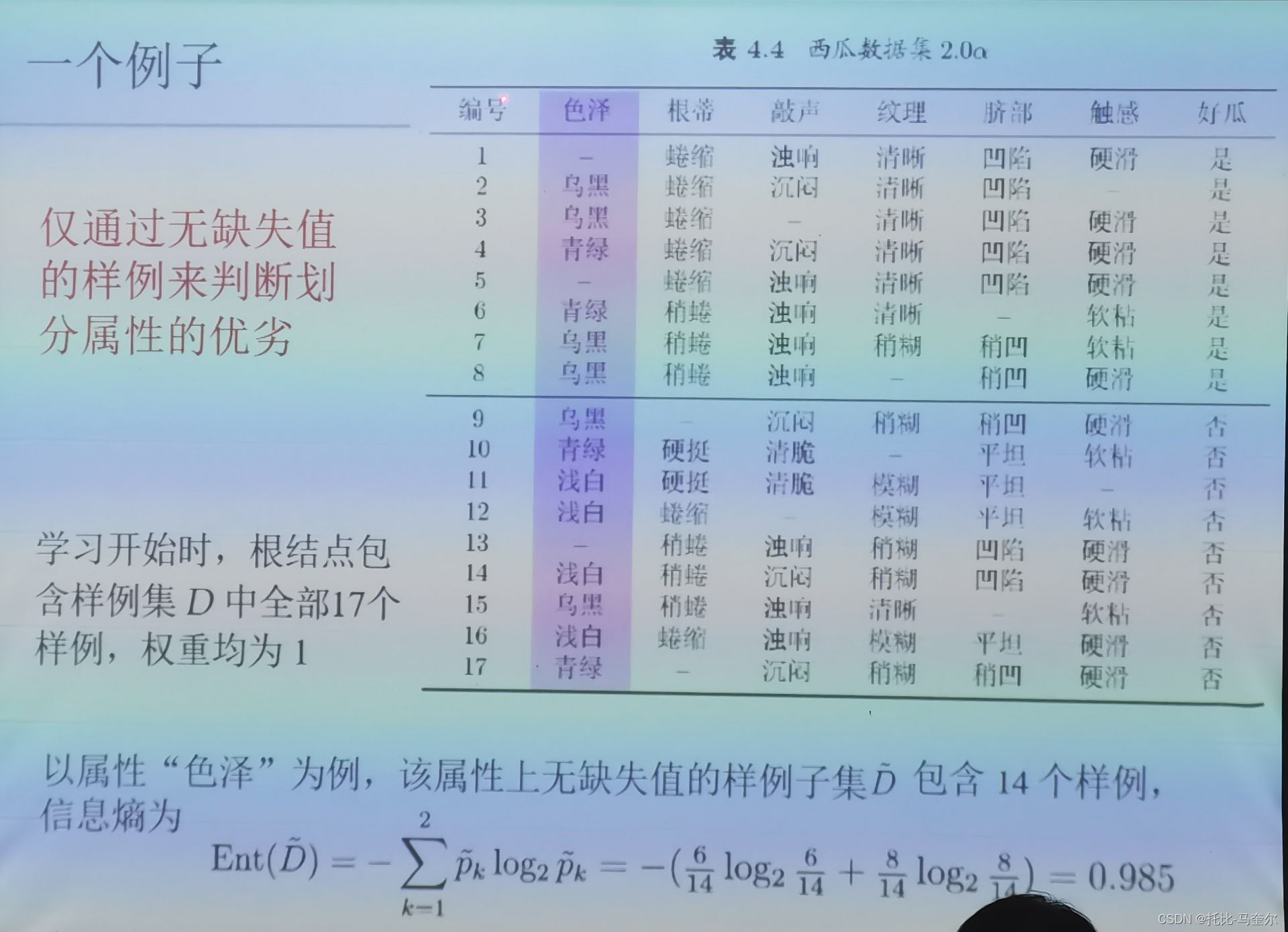
缺失值

现实应用中，经常会遇到属性值“缺失”现象；

选择划分属性的基本思路：样本赋权，权重划分

缺失值计算信息增益

从“树”到“规则”

一棵决策树对应于一个“规则集”

每个从根结点到叶结点的分支路径对应于一条规则

好处：①改善可理解性；②进一步提高泛化能力

多变量决策树

每个分支结点不仅考虑一个属性；“斜决策树”不是为每个非叶节点寻找最佳划分属性，而是建立一个线性分类器

线性回归

$f(x)=wx_{i}+b$ $f(x)\simeq y_{i}$

离散属性的处理：若有“序”，则连续化；否则，转化为k维向量

令均方误差最小化，有 $(w^{*},b^{*})=\frac{1}{m}\sum_{i=1}^{m}(f(x_{i})-y_{i})^2=\frac{1}{m}\sum_{i=1}^{m}(y_{i}-wx_{i}-b)^2$

对 $E_{(w,b)}=\sum_{i=1}^{m}(y_{i}-wx_{i}-b)^2$ 进行最小二乘参数估计

分别对w和b求导：

$\frac{\partial E_{(w,b)}}{\partial w}=2(w\sum_{i=1}^{m}x_{i}^{2}-\sum_{i=1}^{m}(y_{i}-b)x_{i})$

$\frac{\partial E_{(w,b)}}{\partial b}=2(mb-\sum_{i=1}^{m}(y_{i}-wx_{i}))$

令导数为0，得到闭式解：

$w=\frac{\sum_{i=1}^{m}y_{i}(x_{i}-\bar x)}{\sum_{i=1}^{m}x_{i}^{2}-\frac{1}{m}(\sum_{i=1}^{m}x_{i})^{2}}$ ， $b=\frac{1}{m}\sum_{i=1}^{m}(y_{i}-wx_{i})$