代码随想录算法训练营第27天|二叉搜索树、LeetCode700.二叉搜索树中的搜索、LeetCode98.验证二叉搜索树

1、二叉搜索树

二叉搜索树是一个有序树：

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉搜索树

这就决定了，二叉搜索树，递归遍历和迭代遍历和普通二叉树都不一样。

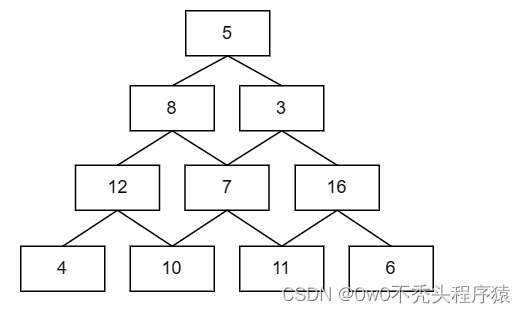
如：

2、LeetCode700.二叉搜索树中的搜索

700. 二叉搜索树中的搜索 - 力扣（LeetCode）

第一想法（递归法）

就是递归遍历二叉搜索树

代码

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        // 空，不存在
        if(!root)   return NULL;
        // 找到
        if(root->val == val)   return root;
        // 递归去找
        if(val < root->val)
            return searchBST(root->left, val);
        if(val > root->val)
            return searchBST(root->right, val);
        return NULL;
    }
};

迭代法

一提到二叉树遍历的迭代法，可能立刻想起使用栈来模拟深度遍历，使用队列来模拟广度遍历。对于二叉搜索树可就不一样了，因为二叉搜索树的特殊性，也就是节点的有序性，可以不使用辅助栈或者队列就可以写出迭代法。

对于一般二叉树，递归过程中还有回溯的过程，例如走一个左方向的分支走到头了，那么要调头，在走右分支。而对于二叉搜索树，不需要回溯的过程，因为节点的有序性就帮我们确定了搜索的方向。

代码

OMG…居然这么短这么简单…

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        // 法2 迭代
        while(root){
            if(val < root->val) root = root->left;
            else if(val > root->val)    root = root->right;
            else return root;
        }
        return root;
    }
};

3、LeetCode98.验证二叉搜索树

98. 验证二叉搜索树 - 力扣（LeetCode）

第一想法

递归地验证。

代码

噢居然一遍过了！！！噢不…额外的测试用例没过，看来是跳进陷阱里面去了

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        if(root == NULL)    return true;
        // 判断左右节点是否符合
        bool left = true;
        bool right = true;
        //左子树
        if(root->left){
            //左节点是否符合
            if(root->left->val >= root->val)
                left = false;
            else
                //左节点合格，左子树是否合格
                left = isValidBST(root->left);
        }
      	//右子树
        if(root->right){
            if(root->right->val <= root->val)
                right = false;
            else
                right = isValidBST(root->right);
        }
      	//左右同时合格才行
        return left && right;
    }
};

犯错的情况：

6比10小，但是却在10的右子树上。

解题思路（递归法）

代码随想录 (programmercarl.com)

中序遍历下，输出的二叉搜索树节点的数值是有序序列。有了这个特性，验证二叉搜索树，就相当于变成了判断一个序列是不是递增的了。

代码：

中序遍历，存入数组。最后判断数组是否是递增的。

class Solution {
private:
    vector<int> vec;
    void traversal(TreeNode* root) {
        if (root == NULL) return;
        traversal(root->left);
        vec.push_back(root->val); // 将二叉搜索树转换为有序数组
        traversal(root->right);
    }
public:
    bool isValidBST(TreeNode* root) {
        vec.clear(); // 不加这句在leetcode上也可以过，但最好加上
        traversal(root);
        for (int i = 1; i < vec.size(); i++) {
            // 注意要小于等于，搜索树里不能有相同元素
            if (vec[i] <= vec[i - 1]) return false;
        }
        return true;
    }
};

还有另外的写法以及迭代法，但是短时间内没看懂，先掌握这一种，下次再来看（代码随想录的网站上）