一般学习过编程的人都知道，排序算法有很多种，包括直接选择排序、直接插入排序、计数排序、快速排序、归并排序、冒泡排序等，在我看来，以上六种排序算法是必须要掌握的，今天，我们先来讲解一下冒泡排序算法，我每次讲解排序算法的时候，都会按四步走，分别是：

（1）学习理解排序原理
（2）举一个例子，模拟排序过程
（3）梳理排序过程中i，j变量的变化
（4）编写代码程序

---

第一步：学习理解冒泡排序的原理（以从小到大排序为例）

将数组中的每个相邻的元素进行两两比较，按照小的元素在前的原则确定这两个元素是否交换。这样每一轮执行之后，最大的元素就会被交换到最后一位。

完成一轮之后，我们就可以再从头进行第二轮的比较，直到倒数第二位时结束（因为最后一位已经是被排序好的了）。这样子一轮之后，第二大的元素就被交换到倒数第二位。

然后以此类推……最终数据全部有序了。

---

根据以上原理的学习，有些人可能感觉到有点抽象，没关系，我们举一个具体的例子来讲解。

第二步：模拟冒泡排序的过程

有一个数组，它的待排元素为：3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48，现在我们要将这组数据进行升序排列，即从小到大排列。

我们可以观察以下动图的排序过程，在排序的过程中，我们可以看到的是，相邻的元素是两两进行比较的，如果左边的元素大于右边的元素，那么就进行交换，否则就不进行交换。

当第一轮排序过后，可以看到50这个最大的数据，已经被排到最后一位了；

当第二轮排序过后，可以看到48这个第二大的数据，已经被排到倒数第二位了；

当第三轮排序过后，可以看到47这个第三大的数据，已经被排到倒数第三位了；

按照原理，以此类推，最终所有的数据都会有序………………记住核心原理，两两比较，大的数据往后冒……

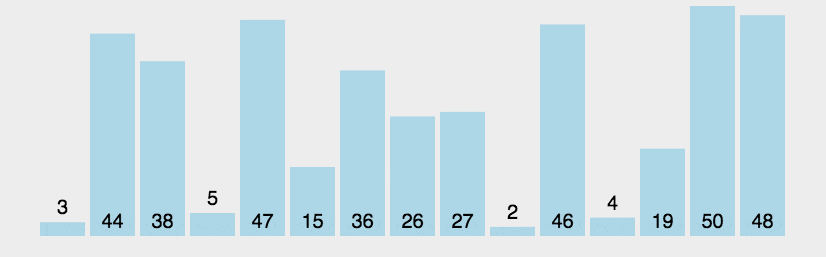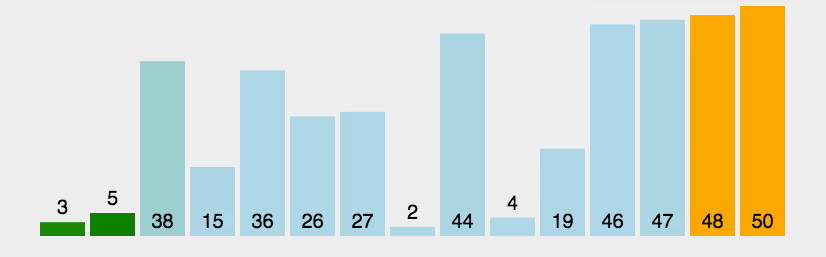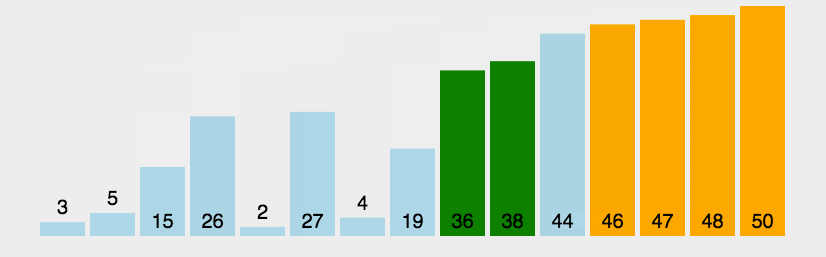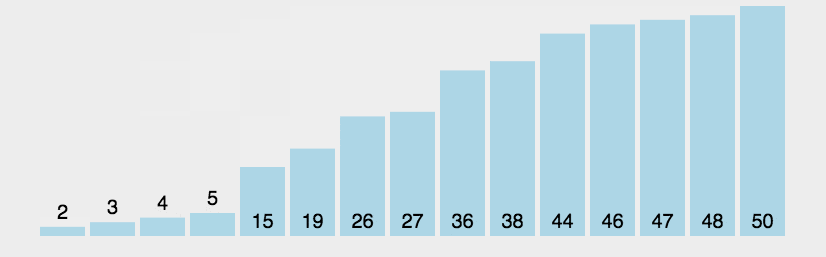
接下来我们一起来思考一个问题，假设我有5, 3, 2 , 4, 1这5个元素，我还是想要对这组数据进行升序排列，那么我需要 进行几轮的排序，才能够使得这组数据有序呢？
第一轮排序：确定5的位置，为最后一位
第二轮排序：确定4的位置，为倒数第二位
第三轮排序：确定3的位置，为倒数第三位
第四轮排序：确定2的位置，为倒数第四位
此时就只剩下1这个元素了，还有必要再进行第五轮排序吗？ 没有必要，因为2 3 4 5已经有序了，自然而然，1这个数字已经落在第一个位置了。于是，我们得出一个结论， 如果你有n个数据，那么只需要进行n-1轮的排序就能够把这n个数据给排列有序。

第三步：梳理排序过程中i，j变量的变化

原理听起来似乎很简单，但是如果进行编写代码的话，我想会难住很多小伙伴。在这里，我用n代表总共要排序的元素个数,i代表循环的轮数，j代表每一轮比较时的下标位置。

在进行代码编写之前，我们先来思考一个问题，对于n个元素，我们需要进行n-1轮的排序，每一轮进行排序的时候，元素需要进行两两的比较，假设当前的元素为a[j]，那么它就应该和a[j+1]这个元素进行比较，对于升序而言，如果a[j]>a[j+1]，那么就需要交换这两个元素的位置，否则就不交换。

第二点，每一轮进行两两比较的时候，都需要比较到最后一个元素吗？当然不一定，比如说还是5,3,2,4,1这5个元素，第一轮排序之后变成：3,2,4,1,5；再进行第二轮排序的时候，因为5已经确定了位置，所以这个时候只需要比较3,2,4,1这4个元素即可，5是已排元素，而3,2,4,1是待排元素，我们只需要比较待排元素就好了。第二轮排序结束之后，序列变为：2,3,1,4,5；再进行第三轮排序的时候，只需要比较2,3,1,这3个元素就好了，4,5这两个已排元素无需再管它。也就说，每一轮的排序过程中，j的取值范围是不一样的，j的取值范围会随着排序的轮数变化而变化，而i就代表排序的轮数，即j会随着i的变化而变化。如果你到这里还是觉得很抽象，没关系，稍后的代码会让你一目了然。

根据上面的分析，我们知道，假设有n个元素，那么需要n-1轮的排序，i的取值是0~n-2，而j的取值是0~n-2-i，可以想象一下，当第一轮排序的时候，此时i=0，j的取值范围从0~n-2。当最后一轮排序的时候，i等于n-2，那么此时j的取值范围为：0~0，j取0，j+1取1，让下标0的元素和下标1的元素进行比较一次即可，这一次做完，数据就全部排序完成了。

注意，在编写代码的过程中，数组不要越界。

---

第四步：编写代码程序

#include<bits/stdc++.h>
using namespace std;
int a[] = {2,5,3,1,7,4,8,9,0,6}; 
void print(int n) {
    for(int i=0;i<n;i++)
        cout << a[i] << " ";
    cout << endl;
}
void bubSort(int n) {
    for(int i=0;i<n-1;i++) {
        bool flag = true;  //假设在这一轮开始之前，序列已经有序 
        for(int j=0;j<n-1-i;j++) {
            if(a[j]>a[j+1]) {
                swap(a[j],a[j+1]);
                flag = false;
            }
        } 
        if(flag==true) {
            break;
        }
        print(n);  //每一轮排序完之后，输出打印查看结果 
    }
}
int main() {
    print(10);
    bubSort(10);
    print(10);
    return 0;
}

代码的编写过程和我讲的有一点不同，不同在我多了一个flag标记变量，它有什么作用呢?它是用来优化我们程序的，我举一个简单的例子，比如有 5 1 2 3 4 ，这5个数，当第一轮排序之后，变成 1 2 3 4 5，可以发现，此时数列已经有序了，接下来还有必要排序吗？显然没有必要了；当第二轮排序的时候发现，这个序列没有任何元素进行交换，说明该序列已经有序了，这个时候我们使用一个标记变量flag来做标记，如果这个标记变量没有改变过，那么这一轮结束，排序算法也可以结束了。第二轮排序完，就可以直接结束排序的过程了，而没有必要进行第3、4轮的排序，继续进行排序也没错，只不过浪费了时间而已。但是时间往往是衡量一个算法最重要的指标。

通过以上的方法，大大提高了冒泡排序的效率，不得不说，冒泡排序算法是一种聪明的排序，当数据有序时，冒泡排序就直接退出了，结束排序过程。

---

你想要检验你的算法是否学习明白了，最好的方式就是去做题，题目我一般是发布在群里，因为会做另外的讲解。如果你对于以上的代码有任何疑问，你可以私信我，或者你想进入我的算法讨论群也可以私信我…如果你只是想在群里呆着，不说话，不互动，那你不要私信我，谢谢！