题目链接：最长斐波那契数列

题目：

输入一个没有重复数字的单调递增的数组，数组中至少有 3 个数字，请问数组中最长的斐波那契数列的长度是多少？例如，如果输入的数组是 [1, 2, 3, 4, 5, 6, 7, 8]，由于其中最长的斐波那契数列是 1、2、3、5、8，因此输出 5。

分析：

所谓斐波那契数列，是指数列中从第三个数字开始每个数字都等于前面两个数字之和，如数列 1、2、3、5、8、13 就是一个斐波那契数列。

可以从左至右每次从输入的数组中取出一个数字，使之和前面的若干数字组成斐波那契数列。一个数字可能和前面不同的数字组成不同的斐波那契数列。例如，输入数组 [1, 2, 3, 4, 5, 6, 7, 8]，假设我们处理到数字 6，数字 6 就可以和前面的数字组成两个斐波那契数列，分别是 1、5、6 和 2、4、6。也就是说，每处理到一个数字时可能面临若干选择，需要从这些选择中找出最长的斐波那契数列。解决一个问题需要多个步骤，每一步面临若干选择，这个题目看起来适合运用回溯法。但由于这个问题没有要求列出所有的斐波那契数列，而是找出最长斐波那契数列的长度，也就是求最优解，因此可以用动态规划来解决这个问题。

分析确定状态转移方程：

应用动态规划的关键在于找出状态转移方程。将数组记为 A，A[i] 表示数组中下标为 i 的数字。对于每个 j（0 <= j < i），A[j] 都有可能是在某个斐波那契数列中 A[i] 前面的一个数字。如果存在一个 k（0 <= k < j）满足 A[k] + A[j] = A[i]，那么这 3 个数字就组成了一个斐波那契数列。这个以 A[i] 为结尾、前一个数字是 A[j] 的斐波那契数列是在以 A[j] 为结尾、前一个数字是 A[k] 的序列的基础上增加一个数字 A[i]，因此前者的长度是在后者的长度的基础上加 1。

例如，在数组 A = [1, 2, 3, 4, 5, 6, 7, 8] 中，A[7] 等于 8。数字 8 既可以在 1、2、3、5（结尾数字为 A[4]）的基础上形成更长的斐波那契数列，也可以和数字 6（A[5]）一起形成斐波那契数列 2、6、8，还可以和数字 7（A[6]）一起组成斐波那契数列 1、7、8。虽然序列 2、6 和 1、7 本身都不是斐波那契数列，但在后面添加数字 8 之后就变成斐波那契数列。

由于以 A[i] 为结尾的斐波那契数列的长度依赖于它前面的数字 A[j]，不同的 A[j] 能和 A[i] 形成不同的斐波那契数列，它们的长度也可能不同。因此，状态转移方程有两个参数 i 和 j，f(i, j) 表示以 A[i] 为最后一个数字、A[j] 为倒数第 2 个数字的斐波那契数列的长度。如果数组中存在一个数字 k，使 A[i] = A[j] + A[k]（0 <= k < j < i），那么 f(i, j) = f(j, k) + 1，即在以 A[j] 为最后一个数字、A[k] 为倒数第 2 个数字的斐波那契数列的基础上增加一个数字 A[i]，形成更长的一个数列。f(i, j) 的值可能是 2，此时虽然 A[i] 和 A[j] 这两个数字现在还不能形成一个有效的斐波那契数列，但可能会在之后增加一个新的数字使之形成长度为 3 甚至更长的斐波那契数列。

根据状态转移方程写代码：

由于状态转移方程有两个参数 i 和 j，因此需要一个二维数组来缓存 f(i, j) 的计算结果。i 对应二维数组的行号，j 对应二维数组的列号。由于 i 大于 j，因此实际上只用到了二维数组的左下角部分。如果数组的长度是 n，那么 i 的取值范围为 1 ~ n - 1，而 j 的取值范围为 0 ~ n - 2。

下表记录了计算数组 [1, 2, 3, 4, 5, 6, 7, 8] 中最长斐波那契数列的长度的过程。

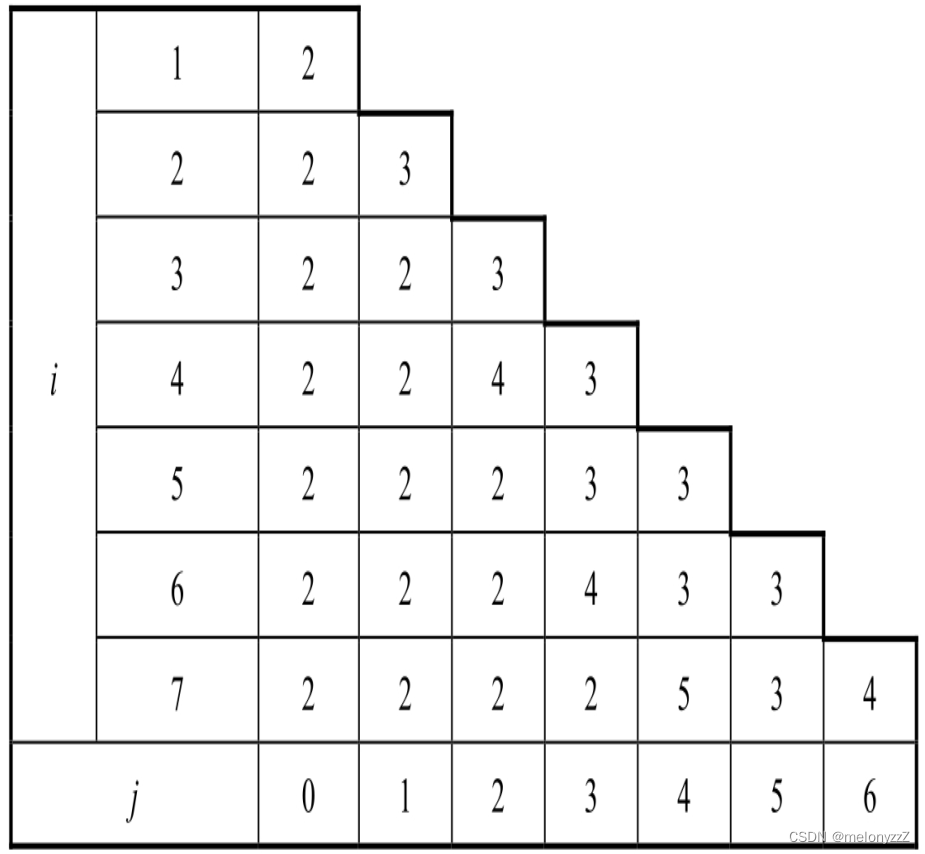
代码实现：

class Solution {
public:
    int lenLongestFibSubseq(vector<int>& arr) {
        unordered_map<int, int> numToIndex;
        numToIndex[arr[0]] = 0;
​
        int n = arr.size();
        vector<vector<int>> dp(n, vector<int>(n - 1));
        int result = 0;
        for (int i = 1; i < n; ++i)
        {
            for (int j = 0; j < i; ++j)
            {
                int target = arr[i] - arr[j];
                if (numToIndex.count(target) && numToIndex[target] < j)
                {
                    int k = numToIndex[target];
                    dp[i][j] = dp[j][k] + 1;
                    result = max(result, dp[i][j]);
                }
                else
                {
                    dp[i][j] = 2;
                }
            }
            numToIndex[arr[i]] = i;
        }
        return result;
    }
};