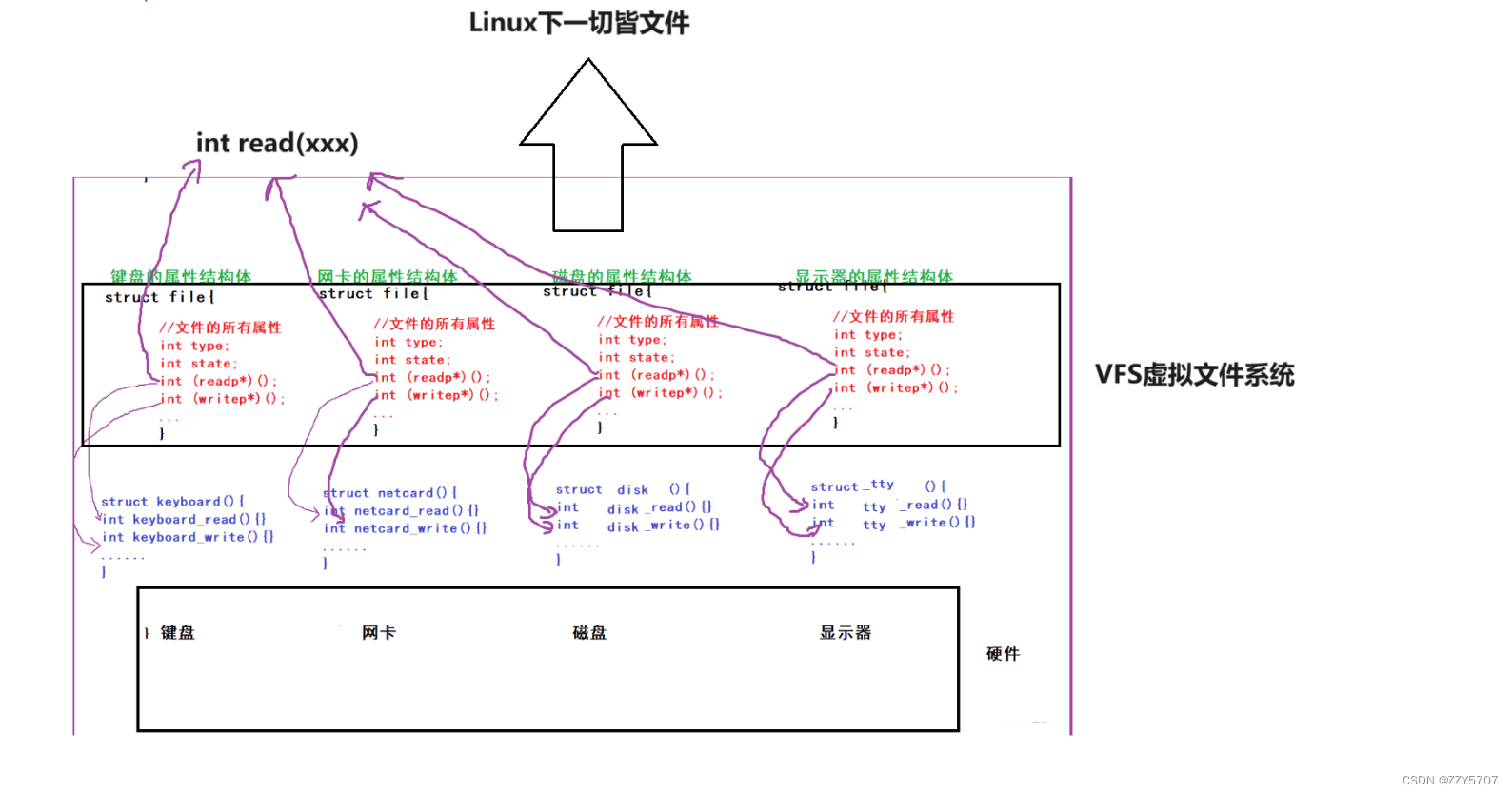
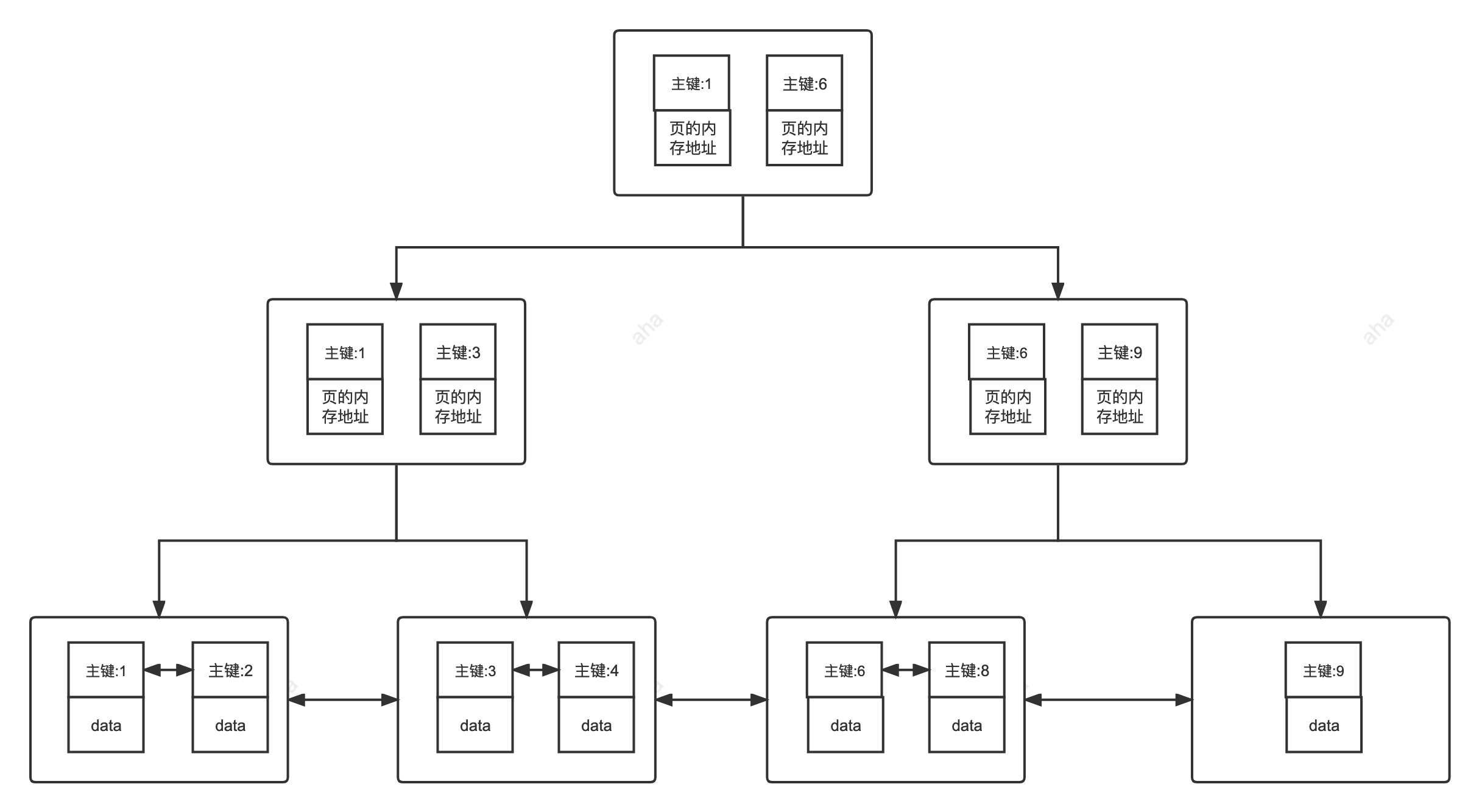
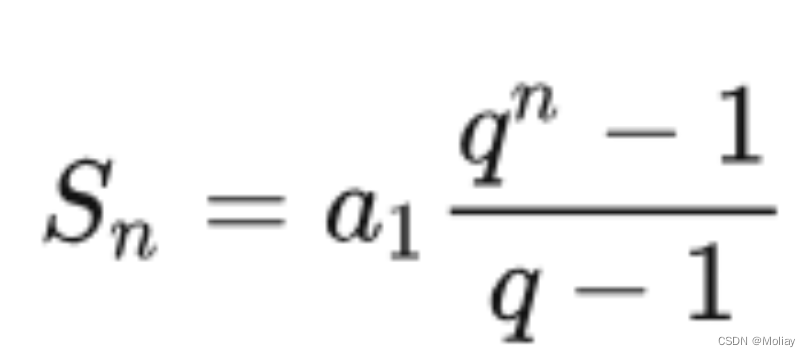哪里存在KV Cache?
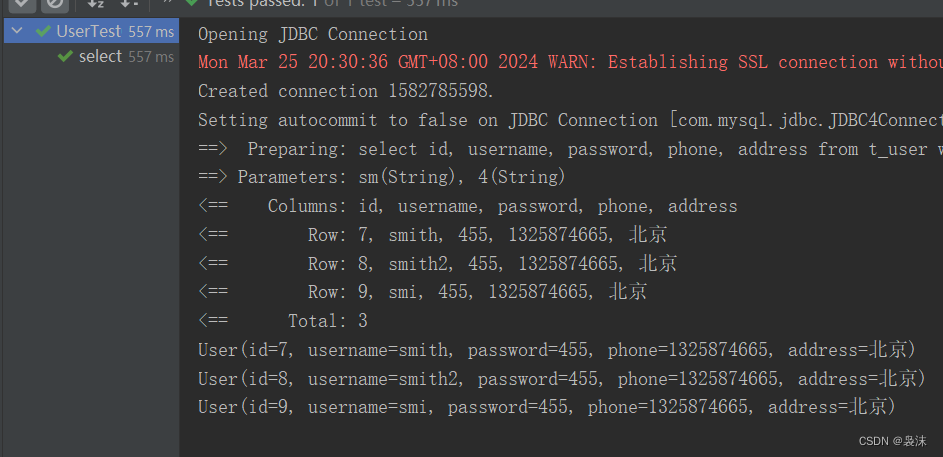
KV cache发生在多个token生成的步骤中,并且只发生在decoder中(例如,decoder-only模型,如 GPT,或在encoder-decoder模型,如T5的decoder部分),BERT这样的encoder模型不是生成式模型(而是判别性模型),因此没有KV cache。
以下动图是GPT-2以自回归形式生成文本的动态图:

下图是Attention的标准计算方式:
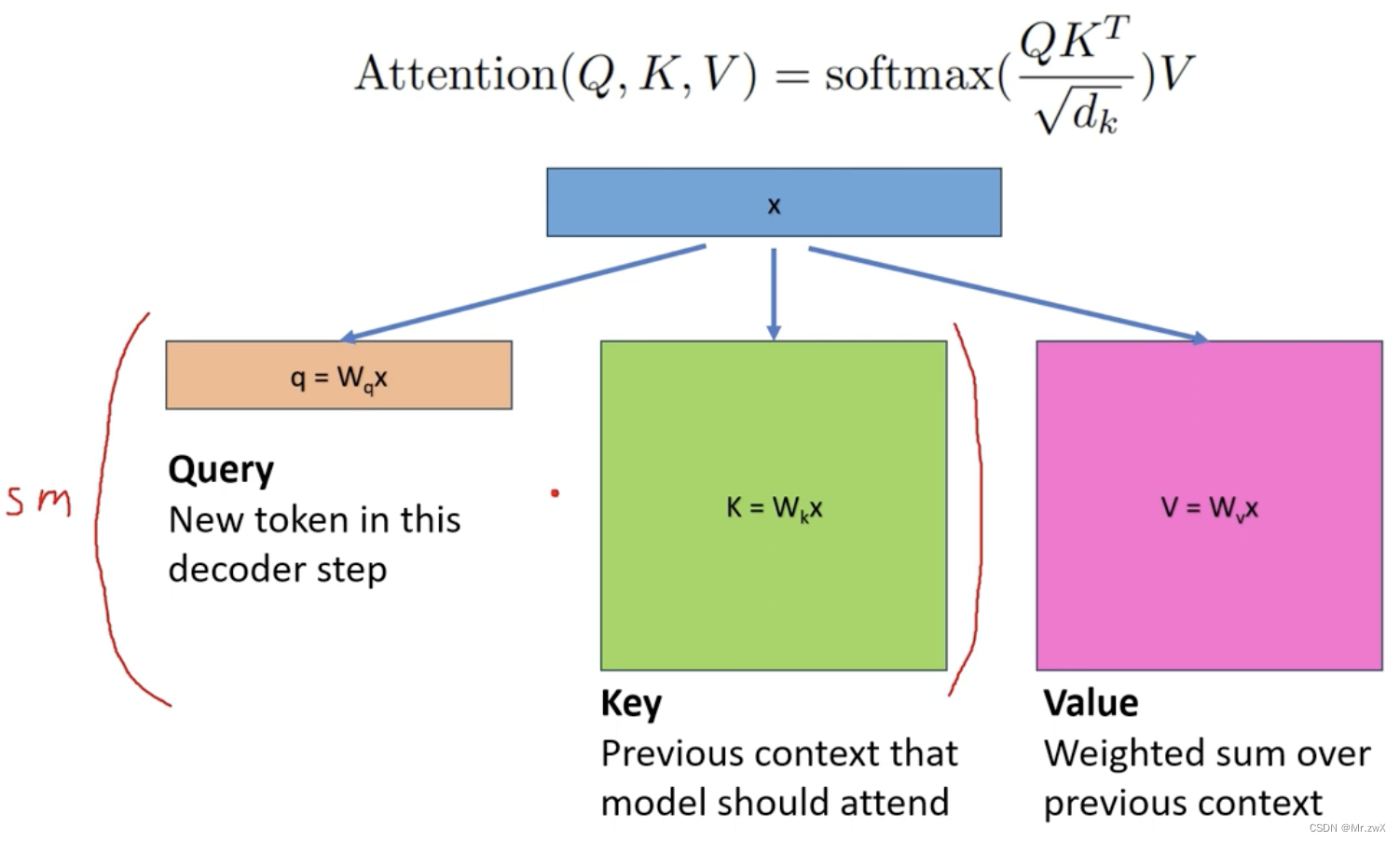
什么是KV Cache?
通过缓存以前的键(Key)和值(Value),我们可以只关注计算新token的注意力。
如下图,每当来一个新的token
q
n
e
w
q_{new}
qnew时,计算得到新的
k
n
e
w
k_{new}
knew和
v
n
e
w
v_{new}
vnew,并将其拼接(concat)到缓存的
K
p
r
e
v
K_{prev}
Kprev和
V
p
r
e
v
V_{prev}
Vprev中。
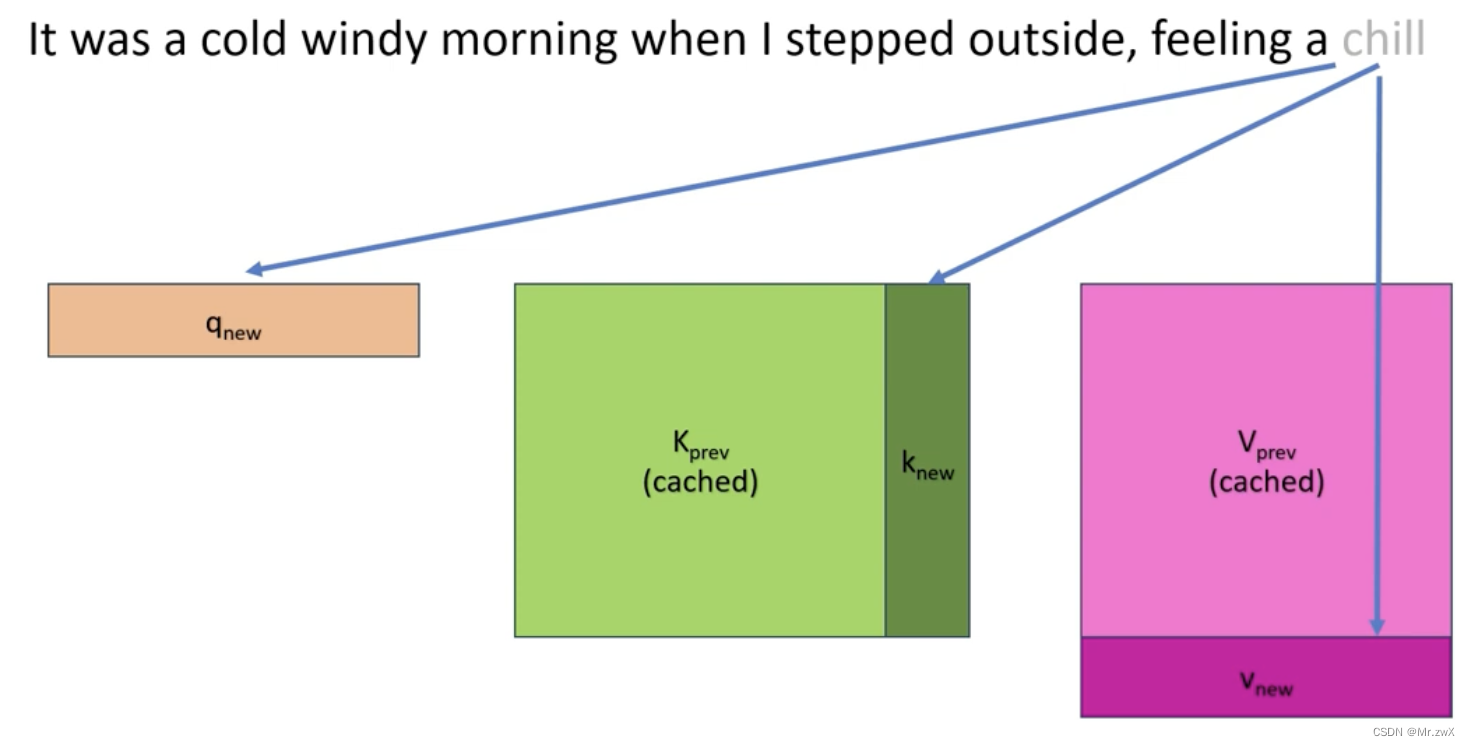

假设
T
T
T是序列长度,
D
D
D是维度(也就是上图的emb_size)。
在没有cache的情况下:
- Q : ( T , D ) Q: (T, D) Q:(T,D)
- K T : ( D , T ) K^T: (D, T) KT:(D,T)
- V : ( T , D ) V: (T, D) V:(T,D)
- Q K T : ( T , T ) QK^T: (T, T) QKT:(T,T)
- A t t e n t i o n : ( T , D ) Attention: (T, D) Attention:(T,D)
可以看到,每来一个新的query token后,都需要重新计算一遍注意力,复杂度是 O ( T 2 ) O(T^2) O(T2),这也就是原始的Transformer平方复杂度。
在有cache的情况下:
- Q : ( 1 , D ) Q: (1, D) Q:(1,D)
- K T : ( D , T ) K^T: (D, T) KT:(D,T)
- V : ( T , D ) V: (T, D) V:(T,D)
- Q K T : ( 1 , T ) QK^T: (1, T) QKT:(1,T)
- A t t e n t i o n : ( 1 , D ) Attention: (1, D) Attention:(1,D)
可以看到,每来一个新的query token后,不需要重新计算一遍注意力,而是只关注计算新token的注意力,复杂度是 O ( T ) O(T) O(T),降低到了线性。
为什么这个优化很重要?
如上图所示,通过KV cache获得的矩阵要比没有KV cache小得多,这导致了更快的矩阵乘法。
Memory Usage分析
Transformer中注意力层中KV的存储开销计算公式:

下面是一个具体的例子,可以看到KV cache的大小竟然是模型的3倍,这在推理场景非常常见。在内存使用中,KV cache往往是主导因素。

参考文档
- Transformers KV Caching Explained
- The KV Cache: Memory Usage in Transformers