【C++练级之路】【Lv.16】红黑树（冰与火的碰撞，红与黑的史诗）

news2024/9/20 9:12:52



快乐的流畅：个人主页


个人专栏：《C语言》《数据结构世界》《进击的C++》

远方有一堆篝火，在为久候之人燃烧！

文章目录

  • 引言
  • 一、红黑树的概念
  • 二、红黑树的模拟实现
    • 2.1 结点
    • 2.2 成员变量
    • 2.3 插入
      • 情况一：uncle在左，parent在右
        • ==如果uncle存在且为红色==：
        • ==如果uncle不存在，或者存在且为黑色==：
      • 情况二：parent在左，uncle在右
        • ==如果uncle存在且为红色==：
        • ==如果uncle不存在，或者存在且为黑色==：
  • 三、红黑树的验证
  • 四、红黑树的性能
    • 4.1 优势
    • 4.2 适用场景

引言

之前学习的AVL树，是一种平衡二叉搜索树，它追求绝对平衡，从而导致插入和删除性能较差。而今天学习的红黑树，是另一种平衡二叉搜索树，它追求相对平衡，使得增删查改的性能都极佳，时间复杂度皆为O(log2N)，是数据结构中的精华，天才般的设想！

一、红黑树的概念

红黑树，顾名思义，其节点有红和黑两种颜色。

之所以新增结点颜色的标记，是因为通过结点着色方式的限制，能够让红黑树的最长路径不超过最短路径的两倍，以保证相对平衡。

红黑树满足五条性质：

  1. 所有结点非黑即红
  2. 根结点为黑色
  3. NIL结点为黑色
  4. 红色结点的子结点必为黑色
  5. 任意结点到其叶子NIL结点的所有路径，都包含相同的黑色结点

在红黑树中，NIL节点（也称为空节点）是叶子节点的一种特殊表示。它们不是实际存储数据的节点，而是树结构中的占位符，用于定义树的边界。所有的红黑树都以NIL节点为叶子节点，这些NIL节点在视觉上通常不被画出来。

性质解读：

  • 性质4：表明不能有连续的红色结点
  • 性质4+性质5：
    • 理论最短路径：全为黑色结点
    • 理论最长路径：红黑相间

这样，就保证了最长路径不超过最短路径的两倍。

二、红黑树的模拟实现

2.1 结点

enum Color
{
	RED,
	BLACK
};

template<class K, class V>
struct RBTreeNode
{
	RBTreeNode<K, V>* _left;
	RBTreeNode<K, V>* _right;
	RBTreeNode<K, V>* _parent;
	pair<K, V> _kv;
	Color _col;

	RBTreeNode(const pair<K, V>& kv)
		: _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _kv(kv)
		, _col(RED)
	{}
};

细节：

  1. 使用三叉链，增加了指向parent的指针
  2. 使用KV模型，数据存储键值对pair
  3. 结点储存颜色，同时颜色使用枚举
  4. 结点的颜色初始化为红色

说明：为什么结点的颜色初始化为红色呢？因为插入新节点时（不为根部），如果插入黑色，就会直接破坏性质5，导致每条路径黑结点数目不同；而如果插入红色，有可能不会破坏性质4，所以结点初始化为红色更优。

2.2 成员变量

template<class K, class V>
class RBTree
{
protected:
	typedef RBTreeNode<K, V> Node;
public:
protected:
	Node* _root = nullptr;
};

2.3 插入

因为红黑树也是二叉搜索树，所以默认成员函数和遍历与之前写的没什么不同，这里重点讲解红黑树的插入。

bool Insert(const pair<K, V>& kv)
{
	if (_root == nullptr)
	{
		_root = new Node(kv);
		_root->_col = BLACK;
		return true;
	}

	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (cur->_kv.first < kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_kv.first > kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			return false;
		}
	}

	cur = new Node(kv);
	if (parent->_kv.first < kv.first)
	{
		parent->_right = cur;
	}
	else
	{
		parent->_left = cur;
	}
	cur->_parent = parent;

	while (parent && parent->_col == RED)
	{
		Node* grandparent = parent->_parent;
		if (grandparent->_right == parent)//uncle在左，parent在右
		{
			Node* uncle = grandparent->_left;
			if (uncle && uncle->_col == RED)//uncle为红，变色+向上调整
			{
				parent->_col = uncle->_col = BLACK;
				grandparent->_col = RED;

				cur = grandparent;
				parent = cur->_parent;
			}
			else//uncle为空或为黑，变色+旋转
			{
				if (parent->_right == cur)//左单旋
				{
					RotateL(grandparent);
					parent->_col = BLACK;
					grandparent->_col = RED;
				}
				else//右左旋
				{
					RotateR(parent);
					RotateL(grandparent);
					cur->_col = BLACK;
					grandparent->_col = RED;
				}
			}
		}
		else//parent在左，uncle在右
		{
			Node* uncle = grandparent->_right;
			if (uncle && uncle->_col == RED)
			{
				parent->_col = uncle->_col = BLACK;
				grandparent->_col = RED;

				cur = grandparent;
				parent = cur->_parent;
			}
			else
			{
				if (parent->_left == cur)//右单旋
				{
					RotateR(grandparent);
					parent->_col = BLACK;
					grandparent->_col = RED;
				}
				else//左右旋
				{
					RotateL(parent);
					RotateR(grandparent);
					cur->_col = BLACK;
					grandparent->_col = RED;
				}
			}
		}
	}
	_root->_col = BLACK;

	return true;
}

思路：

  1. 以二叉搜索树的方式正常插入
  2. 讨论并调整结点的颜色，以及调整结构，使之满足红黑树的性质

循环条件：while (parent && parent->_col == RED)

保证了parent存在且为红，grandparent存在且为黑

情况一：uncle在左，parent在右

如果uncle存在且为红色：

处理方法：

  1. 将parent和uncle变黑，grandparent变红
  2. cur = grandparent，parent = cur->_parent，继续向上调整
  3. 防止grandparent为根节点却变红，在循环结束后将根节点变为黑色
如果uncle不存在，或者存在且为黑色：

当cur在右部外侧时：

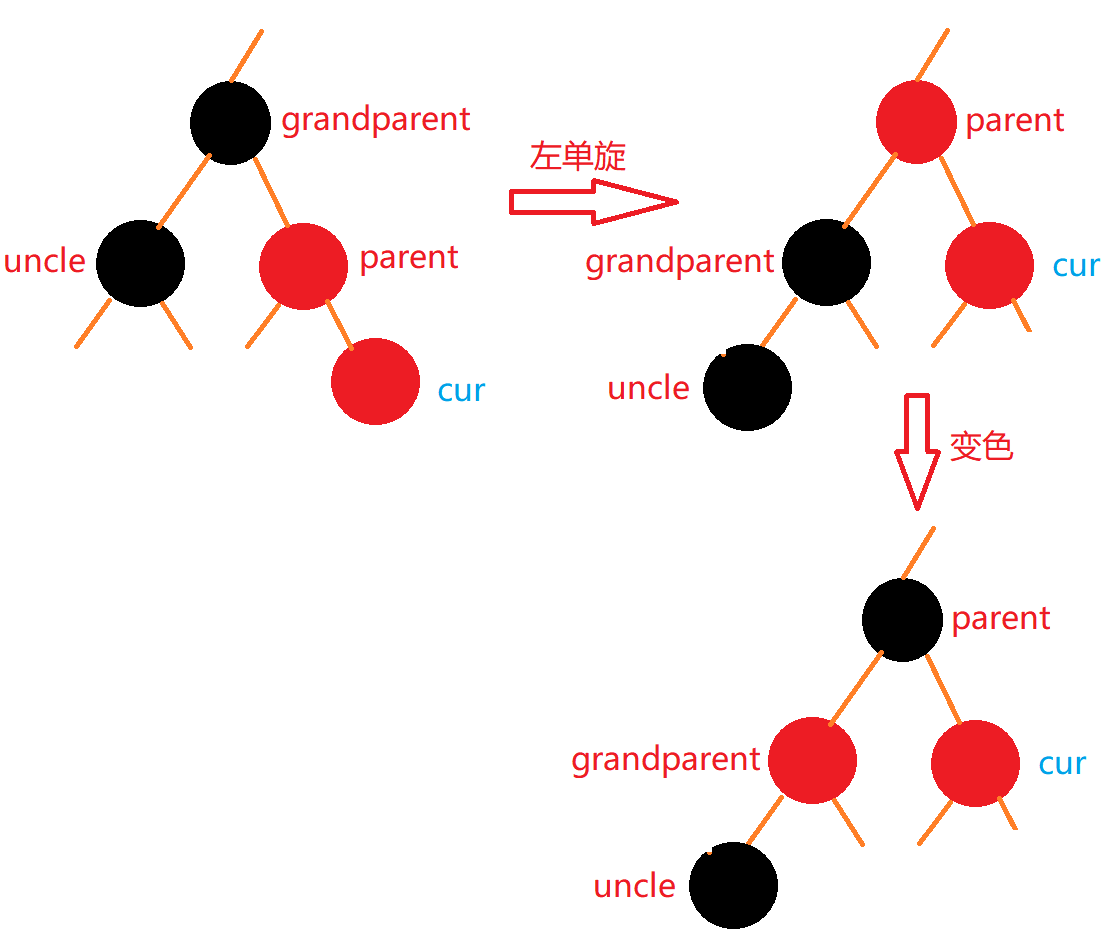
处理方法：

  1. 先对grandparent进行左单旋
  2. 再将parent变黑，grandparent变红

当cur在右部内侧时：

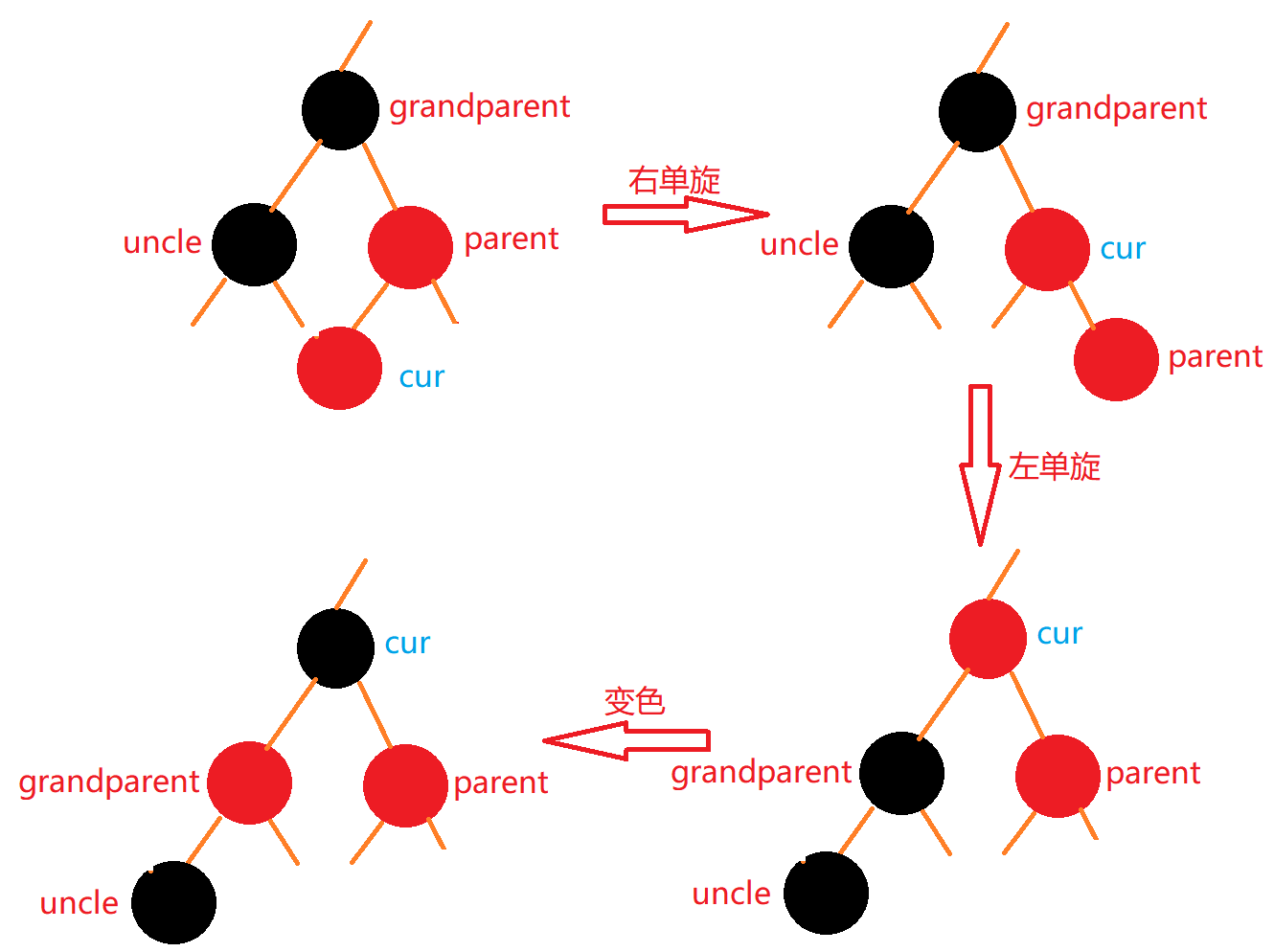
处理方法：

  1. 先对parent进行右单旋
  2. 再对grandparent进行左单旋
  3. 最后将cur变黑，grandparent变红

情况二：parent在左，uncle在右

如果uncle存在且为红色：

处理方法：

  1. 将parent和uncle变黑，grandparent变红
  2. cur = grandparent，parent = cur->_parent，继续向上调整
  3. 防止grandparent为根节点却变红，在循环结束后将根节点变为黑色
如果uncle不存在，或者存在且为黑色：

当cur在左部外侧时：

处理方法：

  1. 先对grandparent进行右单旋
  2. 再将parent变黑，grandparent变红

当cur在左部内侧时：

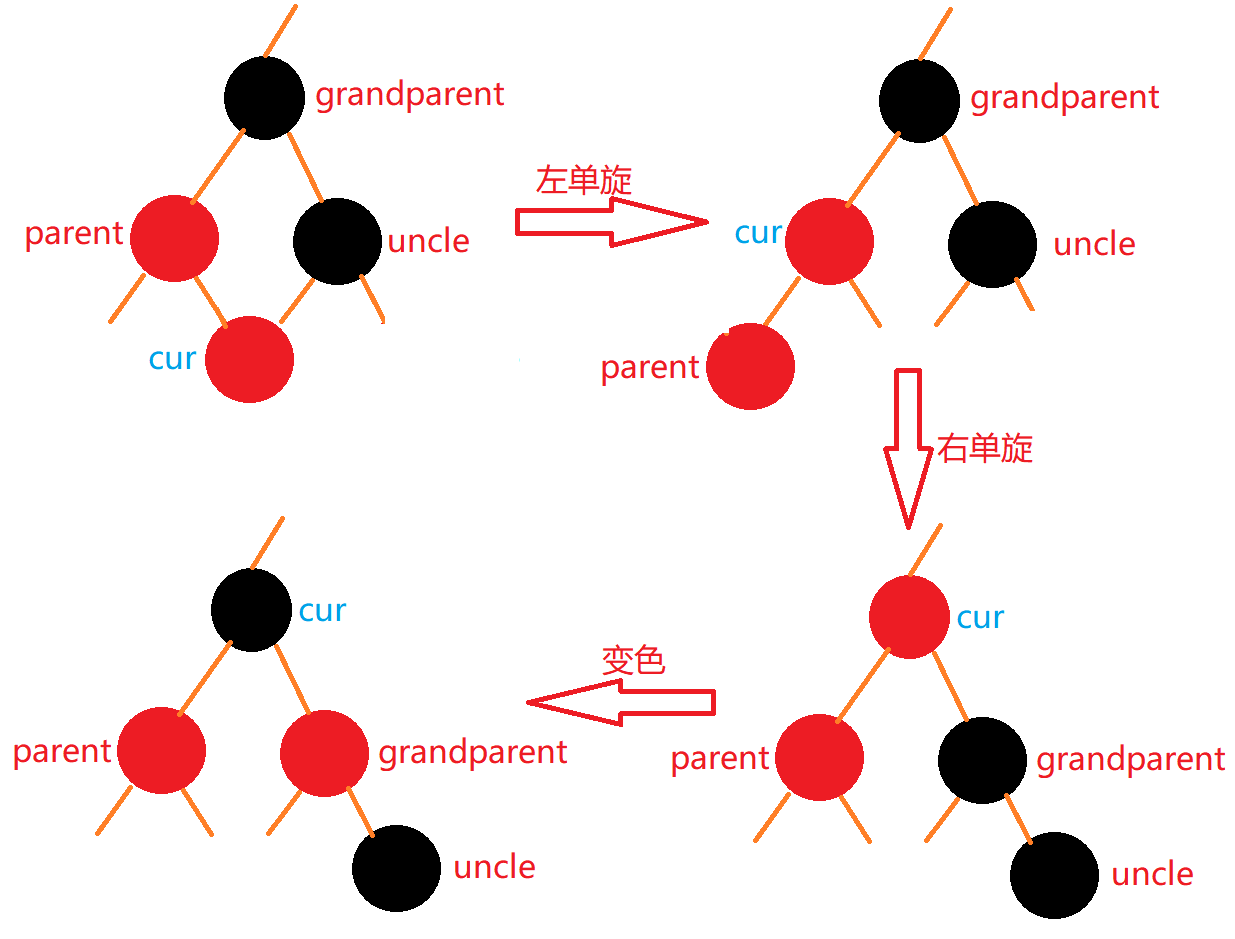
处理方法：

  1. 先对parent进行左单旋
  2. 再对grandparent进行右单旋
  3. 最后将cur变黑，grandparent变红

红黑树插入的核心口诀：uncle存在且为红，变色+向上调整，uncle不存在或为黑，变色+旋转

附上旋转的实现：

void RotateL(Node* parent)
{
	Node* grandparent = parent->_parent;
	Node* subR = parent->_right;
	Node* subRL = subR->_left;

	parent->_right = subRL;
	if (subRL)
	{
		subRL->_parent = parent;
	}

	subR->_left = parent;
	parent->_parent = subR;

	if (grandparent)
	{
		if (grandparent->_right == parent)
		{
			grandparent->_right = subR;
		}
		else
		{
			grandparent->_left = subR;
		}
	}
	else
	{
		_root = subR;
	}
	subR->_parent = grandparent;
}

void RotateR(Node* parent)
{
	Node* grandparent = parent->_parent;
	Node* subL = parent->_left;
	Node* subLR = subL->_right;

	parent->_left = subLR;
	if (subLR)
	{
		subLR->_parent = parent;
	}

	subL->_right = parent;
	parent->_parent = subL;

	if (grandparent)
	{
		if (grandparent->_right == parent)
		{
			grandparent->_right = subL;
		}
		else
		{
			grandparent->_left = subL;
		}
	}
	else
	{
		_root = subL;
	}
	subL->_parent = grandparent;
}

三、红黑树的验证

bool IsBalance()
{
	if (_root && _root->_col == RED)
	{
		cout << "根结点为红色" << endl;
		return false;
	}

	int benchMark = 0;//基准值
	Node* cur = _root;
	while (cur)
	{
		if (cur->_col == BLACK)
		{
			++benchMark;
		}
		cur = cur->_right;
	}

	return Check(_root, 0, benchMark);
}

bool Check(Node* root, int blackNum, int benchMark)
{
	if (root == nullptr)
	{
		if (blackNum != benchMark)
		{
			cout << "某条路径黑色结点数量不相等" << endl;
			return false;
		}
		return true;
	}

	if (root->_col == BLACK)
	{
		++blackNum;
	}

	if (root->_col == RED && root->_parent && root->_parent->_col == RED)
	{
		cout << "存在连续的红色结点" << endl;
		return false;
	}

	return Check(root->_left, blackNum, benchMark)
		&& Check(root->_right, blackNum, benchMark);
}

细节：

  1. 验证根节点是否为黑
  2. 先计算出一条路径的黑色结点个数作为基准值，再在递归中比较每条路径的黑色结点是否相等
  3. 若该节点为红，检测其parent是否为红，判断是否存在连续的红色节点

四、红黑树的性能

4.1 优势

红黑树是高效的平衡二叉树，增删改查的时间复杂度都是O( l o g 2 N log_2 N log2​N)，红黑树不追求绝对平衡，其只需保证最长路径不超过最短路径的2倍，相对AVL树而言，降低了插入和旋转的次数。

4.2 适用场景

因此，在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。


真诚点赞，手有余香

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1544728.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Linux-进程控制（进程创建、进程终止、进程等待）

Linux-进程控制（进程创建、进程终止、进程等待）

一、进程创建 1.1 fork函数介绍 在命令行下我们可以通过 ./ exe文件 来创建一个进程&#xff0c;通过fork函数&#xff0c;我们可以通过代码的形式从一个进程中创建一个进程&#xff0c;新进程为子进程&#xff0c;原进程为父进程&#xff0c;子进程在创建时&#xff0c;会与…
阅读更多...
LabVIEW智能降噪系统

LabVIEW智能降噪系统

LabVIEW智能降噪系统 随着噪声污染问题的日益严重&#xff0c;寻找有效的降噪技术变得尤为关键。介绍了一种基于LabVIEW平台开发的智能降噪系统&#xff0c;该系统能够实时采集环境噪声&#xff0c;并通过先进的信号处理技术实现主动降噪&#xff0c;从而有效改善生活和工作环…
阅读更多...
Stable Diffusion 进阶教程 - 二次开发（制作您的文生图应用）

Stable Diffusion 进阶教程 - 二次开发（制作您的文生图应用）

目录 1. 引言 2. 基于Rest API 开发 2.1 前置条件 2.2 代码实现 2.3 效果演示 2.4 常见错误 3. 总结 1. 引言 Stable Diffusion作为一种强大的文本到图像生成模型&#xff0c;已经在艺术、设计和创意领域引起了广泛的关注和应用。然而&#xff0c;对于许多开发者来说&#xff…
阅读更多...
『Apisix入门篇』从零到一掌握Apache APISIX：架构解析与实战指南

『Apisix入门篇』从零到一掌握Apache APISIX：架构解析与实战指南

&#x1f4e3;读完这篇文章里你能收获到&#xff1a; &#x1f310; 深入Apache APISIX架构&#xff1a; 从Nginx到OpenResty&#xff0c;再到etcd&#xff0c;一站式掌握云原生API网关的构建精髓&#xff0c;领略其层次化设计的魅力。 &#x1f50c; 核心组件全解析&#xff…
阅读更多...
深入了解 Linux 中的 MTD 设备：/dev/mtd* 与 /dev/mtdblock*

深入了解 Linux 中的 MTD 设备：/dev/mtd* 与 /dev/mtdblock*

目录 前言一、什么是MTD子系统&#xff1f;二、 /dev/mtd* 设备文件用途注意事项 三、/dev/mtdblock* 设备文件用途注意事项 三、这两种设备文件的关系四、关norflash的一些小知识 前言 在嵌入式Linux系统的世界里&#xff0c;非易失性存储技术扮演着至关重要的角色。MTD&#…
阅读更多...
4.2 循环语句loop，等差数列求和

4.2 循环语句loop，等差数列求和

汇编语言 1. 循环语句loop loop指令的格式是&#xff1a;loop 标号&#xff0c;CPU执行loop指令的时候&#xff0c;要进行两部操作 cx cx - 1;判断cx中的值&#xff0c;不为0则转至标号处执行程序&#xff0c;如果为0则向下执行 循环使用loop来实现&#xff0c;循环次数存…
阅读更多...
基于深度学习的OCR，如何解决图像像素差的问题？

基于深度学习的OCR，如何解决图像像素差的问题？

基于深度学习的OCR技术在处理图像像素差的问题时确实面临一定的挑战。图像像素差可能导致OCR系统无法准确识别文本&#xff0c;从而影响其精度和可靠性。尽管已经有一些方法如SRN-Deblur、超分SR和GAN系列被尝试用于解决这个问题&#xff0c;但效果并不理想。然而&#xff0c;这…
阅读更多...
上位机图像处理和嵌入式模块部署（qmacvisual拟合圆和拟合椭圆）

上位机图像处理和嵌入式模块部署（qmacvisual拟合圆和拟合椭圆）

【 声明&#xff1a;版权所有&#xff0c;欢迎转载&#xff0c;请勿用于商业用途。 联系信箱&#xff1a;feixiaoxing 163.com】 前面我们学习了拟合直线&#xff0c;今天继续学习下拟合圆和拟合椭圆。其实除了最后一步不同&#xff0c;两者的逻辑是差不多的。一般都是&#xf…
阅读更多...
矩阵螺旋输出

矩阵螺旋输出

问题描述&#xff1a; 所谓螺旋矩阵&#xff0c;顾名思义&#xff0c;就是将矩阵元素以螺旋顺序输出&#xff0c;如图&#xff1a; 解决思路&#xff1a; 由图不难发现&#xff0c;整个螺旋输出过程是一个个左下右上遍历的循环&#xff0c;只是遍历的规模在越变越小&#xff…
阅读更多...
2.7、创建列表（List）

2.7、创建列表（List）

概述 列表是一种复杂的容器&#xff0c;当列表项达到一定数量&#xff0c;内容超过屏幕大小时&#xff0c;可以自动提供滚动功能。它适合用于呈现同类数据类型或数据类型集&#xff0c;例如图片和文本。在列表中显示数据集合是许多应用程序中的常见要求&#xff08;如通讯录、…
阅读更多...
分享全栈开发医疗小程序 -带源码课件（课件无解压密码），自行速度保存

分享全栈开发医疗小程序 -带源码课件（课件无解压密码），自行速度保存

课程介绍 分享全栈开发医疗小程序 -带源码课件&#xff08;课件无解压密码&#xff09;&#xff0c;自行速度保存&#xff01;看到好多坛友都在求SpringBoot2.X Vue UniAPP&#xff0c;全栈开发医疗小程序 - 带源码课件&#xff0c;我看了一下&#xff0c;要么链接过期&…
阅读更多...
SpringBoot集成Solr全文检索

SpringBoot集成Solr全文检索

SrpingBoot 集成 Solr 实现全文检索 一、核心路线 使用 Docker 镜像部署 Solr 8.11.3 版本服务使用 ik 分词器用于处理中文分词使用 spring-boot-starter-data-solr 实现增删改查配置用户名密码认证使用 poi 和 pdfbox 组件进行文本内容读取文章最上方有源码和 ik 分词器资源…
阅读更多...
pe启动盘破解windows密码wins电脑登录密码修改重置

pe启动盘破解windows密码wins电脑登录密码修改重置

目录 1.进入电脑BIOS&#xff0c;设置电脑第一启动项为U盘启动2.进入微pe系统3.然后点击界面最左下方的Windows图标4.点击windows密码选择对应用户名称修改&#xff1b; 1.进入电脑BIOS&#xff0c;设置电脑第一启动项为U盘启动 把u盘插到要清除密码的电脑&#xff0c;然后开机…
阅读更多...
面试八股——Redis——分布式锁——Redisson

面试八股——Redis——分布式锁——Redisson

1.看门狗机制 注意看门狗机制&#xff1a;redisson会监听持有锁的线程&#xff0c;并每隔一段时间(releaseTime/3&#xff0c;默认releaseTime为30s)&#xff0c;如果线程还未释放锁的话&#xff0c;会给锁做一次续期。 2. 主从一致性 实际开发中我们会搭建多台redis服务器&a…
阅读更多...
【数据结构】非线性结构——二叉树

【数据结构】非线性结构——二叉树

文章目录 前言1.树型结构1.1树的概念1.2树的特性1.3树的一些性质1.4树的一些表示形式1.5树的应用2.二叉树 2.1 概念2.2 两种特殊的二叉树2.3 二叉树的性质2.4 二叉树的存储2.5 二叉树的基本操作 前言 前面我们都是学的线性结构的数据结构&#xff0c;接下来我们就需要来学习非…
阅读更多...
安防监控视频汇聚平台EasyCVR在银河麒麟V10系统中的启动异常及解决方法

安防监控视频汇聚平台EasyCVR在银河麒麟V10系统中的启动异常及解决方法

安防监控视频平台EasyCVR具备较强的兼容性&#xff0c;它可以支持国标GB28181、RTSP/Onvif、RTMP&#xff0c;以及厂家的私有协议与SDK&#xff0c;如&#xff1a;海康ehome、海康sdk、大华sdk、宇视sdk、华为sdk、萤石云sdk、乐橙sdk等。平台兼容性强&#xff0c;支持Windows系…
阅读更多...
密码学及其应用1 —— 密码学概述

密码学及其应用1 —— 密码学概述

1 密码学的基本概念 1.1 网络安全的定义 网络安全是网络领域的一个专业领域&#xff0c;它涵盖了在基础计算机网络基础设施中所采取的措施、网络管理员为保护网络及网络可访问资源免受未授权访问而采纳的政策&#xff0c;以及对其有效性&#xff08;或无效性&#xff09;的持续…
阅读更多...
WSL2 设置桥接模式

WSL2 设置桥接模式

文章目录 一、前言二、准备阶段三、环境配置3.1 Type-V管理器环境配置3.2 新增.wslconfig 文件 四、遇到的问题以及解决方案 一、前言 ​ 使用 wsl 的过程中&#xff0c;会出现 WSL 的IP地址 找不到&#xff0c;或者无法和计算机通讯&#xff0c;搞 嵌入式 的话&#xff0c;还…
阅读更多...
基于nodejs+vue智能菜谱推荐系统python-flask-django-php

基于nodejs+vue智能菜谱推荐系统python-flask-django-php

本文拟采用nodejs技术和express 搭建系统框架&#xff0c;后台使用MySQL数据库进行信息管理&#xff0c;设计开发的智能菜谱推荐系统。通过调研和分析&#xff0c;系统拥有管理员和用户两个角色&#xff0c;主要具备登录注册、个人信息修改、对用户管理、类型管理、菜谱信息管理…
阅读更多...
力扣算题【第二期】

力扣算题【第二期】

文章目录 1.反转链表1.1 算法题目1.2 算法思路1.3 代码实现 2.回文链表2.1 算法题目2.2 算法思路2.3 代码实现 1.反转链表 1.1 算法题目 给你单链表的头节点 head &#xff0c;请你反转链表&#xff0c;并返回反转后的链表。 1.2 算法思路 1.设置工作指针p,来遍历链表。 2.采…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023