代码随想录算法训练营第33天|1005.K次取反后最大化的数组和|134. 加油站|135. 分发糖果
1005.K次取反后最大化的数组和
本题简单一些,估计大家不用想着贪心 ,用自己直觉也会有思路。
https://programmercarl.com/1005.K%E6%AC%A1%E5%8F%96%E5%8F%8D%E5%90%8E%E6%9C%80%E5%A4%A7%E5%8C%96%E7%9A%84%E6%95%B0%E7%BB%84%E5%92%8C.html
class Solution {
static bool cmp(int a,int b)
{
return abs(a)>abs(b);
}
public:
int largestSumAfterKNegations(vector<int>& nums, int k) {
sort(nums.begin(),nums.end(),cmp);
for(int i=0;i<nums.size();i++)
{
if(nums[i]<0&&k>0)
{
nums[i]=nums[i]*(-1);
k--;
}
}
if(k%2==1) nums[nums.size()-1]*=-1;
int result=0;
for (int a : nums) result += a;
return result;
}
};
那么本题的解题步骤为:
第一步:将数组按照绝对值大小从大到小排序,注意要按照绝对值的大小
第二步:从前向后遍历,遇到负数将其变为正数,同时K–
第三步:如果K还大于0,那么反复转变数值最小的元素,将K用完
第四步:求和
134. 加油站
本题有点难度,不太好想,推荐大家熟悉一下方法二
https://programmercarl.com/0134.%E5%8A%A0%E6%B2%B9%E7%AB%99.html
class Solution {
public:
int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
int cursum=0;
int totalsum=0;
int start=0;
for(int i=0;i<gas.size();i++)
{
cursum+=gas[i]-cost[i];
totalsum+=gas[i]-cost[i];
if(cursum<0) // 当前累加rest[i]和 curSum一旦小于0
{
start=i+1;// 起始位置更新为i+1
cursum=0;// curSum从0开始
}
}
if(totalsum<0) return -1;// 说明怎么走都不可能跑一圈了
return start;
}
};
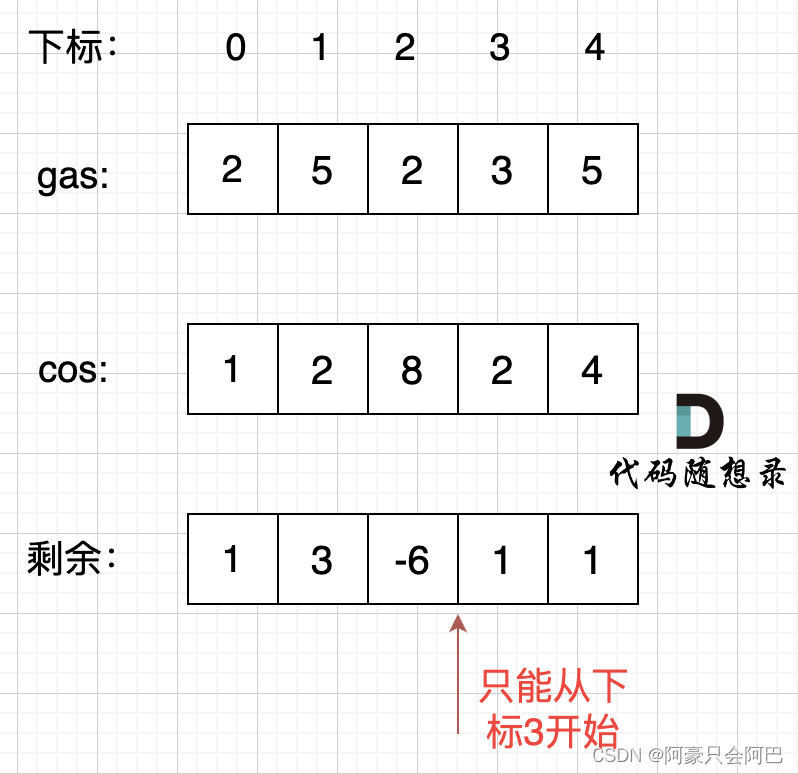
那么为什么一旦[0,i] 区间和为负数,起始位置就可以是i+1呢,i+1后面就不会出现更大的负数?
如果出现更大的负数,就是更新i,那么起始位置又变成新的i+1了。
那有没有可能 [0,i] 区间 选某一个作为起点,累加到 i这里 curSum是不会小于零呢?
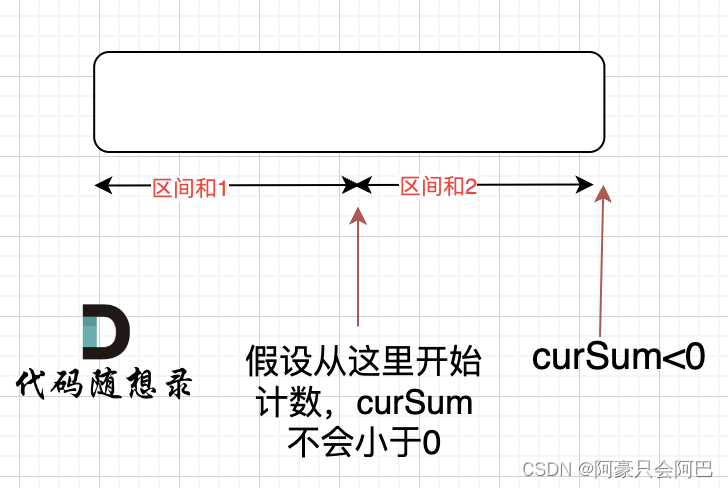
如果 curSum<0 说明 区间和1 + 区间和2 < 0, 那么 假设从上图中的位置开始计数curSum不会小于0的话,就是 区间和2>0。
区间和1 + 区间和2 < 0 同时 区间和2>0,只能说明区间和1 < 0, 那么就会从假设的箭头初就开始从新选择其实位置了。
那么局部最优:当前累加rest[i]的和curSum一旦小于0,起始位置至少要是i+1,因为从i之前开始一定不行。全局最优:找到可以跑一圈的起始位置。
局部最优可以推出全局最优,找不出反例,试试贪心!
135. 分发糖果
本题涉及到一个思想,就是想处理好一边再处理另一边,不要两边想着一起兼顾,后面还会有题目用到这个思路
https://programmercarl.com/0135.%E5%88%86%E5%8F%91%E7%B3%96%E6%9E%9C.html
class Solution {
public:
int candy(vector<int>& ratings) {
vector<int> candyvec(ratings.size(),1);
// 从前向后
for(int i=1;i<ratings.size();i++)
{
if(ratings[i-1]<ratings[i])
candyvec[i]=candyvec[i-1]+1;
}
// 从后向前
for(int i=ratings.size()-2;i>=0;i--)
{
if(ratings[i]>ratings[i+1])
candyvec[i]=max(candyvec[i],candyvec[i+1]+1);
}
// 统计结果
int result=0;
for(int i=0;i<candyvec.size();i++)
result+=candyvec[i];
return result;
}
};
先确定右边评分大于左边的情况(也就是从前向后遍历)
此时局部最优:只要右边评分比左边大,右边的孩子就多一个糖果,全局最优:相邻的孩子中,评分高的右孩子获得比左边孩子更多的糖果
局部最优可以推出全局最优。
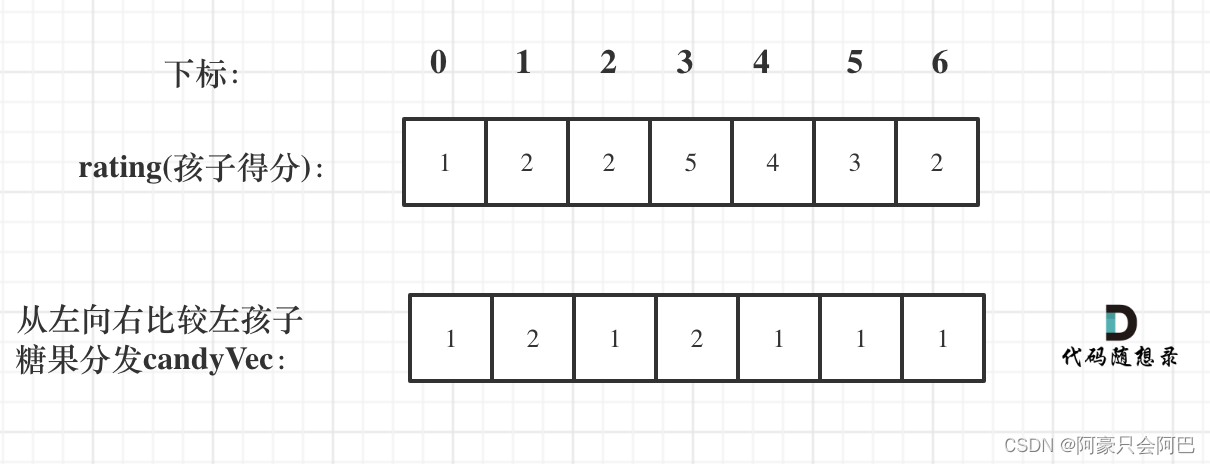
再确定左孩子大于右孩子的情况(从后向前遍历)
遍历顺序这里有同学可能会有疑问,为什么不能从前向后遍历呢?
因为 rating[5]与rating[4]的比较 要利用上 rating[5]与rating[6]的比较结果,所以 要从后向前遍历。
如果从前向后遍历,rating[5]与rating[4]的比较 就不能用上 rating[5]与rating[6]的比较结果了 。
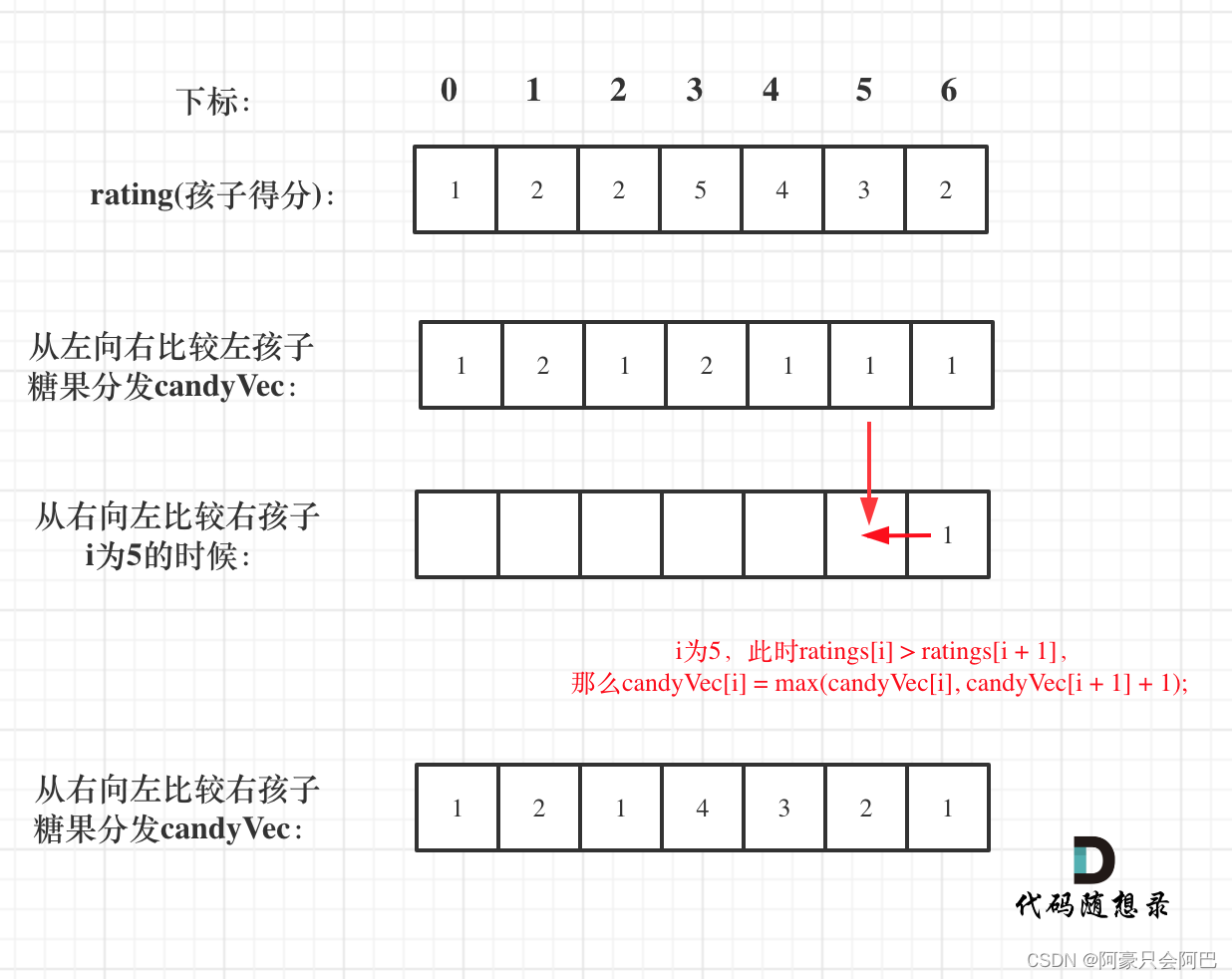
所以确定左孩子大于右孩子的情况一定要从后向前遍历!
如果 ratings[i] > ratings[i + 1],此时candyVec[i](第i个小孩的糖果数量)就有两个选择了,一个是candyVec[i + 1] + 1(从右边这个加1得到的糖果数量),一个是candyVec[i](之前比较右孩子大于左孩子得到的糖果数量)。
那么又要贪心了,局部最优:取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,保证第i个小孩的糖果数量既大于左边的也大于右边的。全局最优:相邻的孩子中,评分高的孩子获得更多的糖果。
局部最优可以推出全局最优。
所以就取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,candyVec[i]只有取最大的才能既保持对左边candyVec[i - 1]的糖果多,也比右边candyVec[i + 1]的糖果多。
如图:

![解决Dev-C++读取输入直到文件结束 while (scanf(“%s“, str[num]) != EOF)没反应的情况](https://img-blog.csdnimg.cn/direct/b4d3222af2124d758d576b11db93e579.png)