机器学习-05-回归算法

总结

本系列是机器学习课程的系列课程，主要介绍机器学习中回归算法，包括线性回归，岭回归，逻辑回归等部分。

参考

fit_transform,fit,transform区别和作用详解！！！！！！

机器学习入门（七）：多项式回归, PolynomialFeatures详解

“L1和L2正则化”直观理解

解读正则化 LASSO回归岭回归

python学习之利用sklearn库自带的函数实现典型回归的回归算法（线性回归，lasso回归，岭回归）

利用sklearn实现逻辑回归

本门课程的目标

完成一个特定行业的算法应用全过程：

懂业务+会选择合适的算法+数据处理+算法训练+算法调优+算法融合
+算法评估+持续调优+工程化接口实现

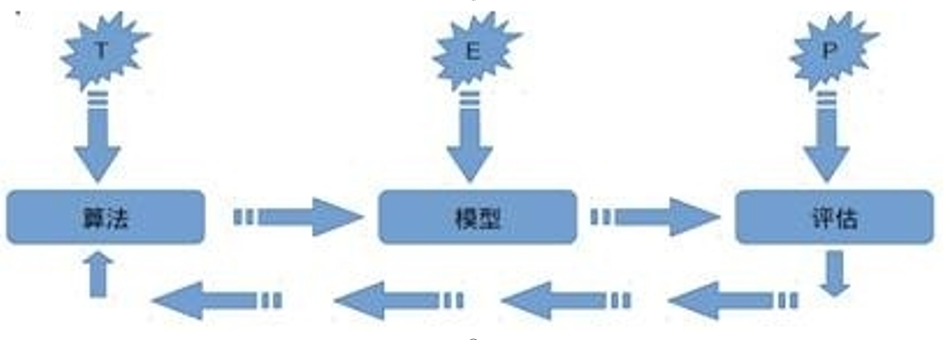
机器学习定义

关于机器学习的定义，Tom Michael Mitchell的这段话被广泛引用：
对于某类任务T和性能度量P，如果一个计算机程序在T上其性能P随着经验E而自我完善，那么我们称这个计算机程序从经验E中学习。

回归算法

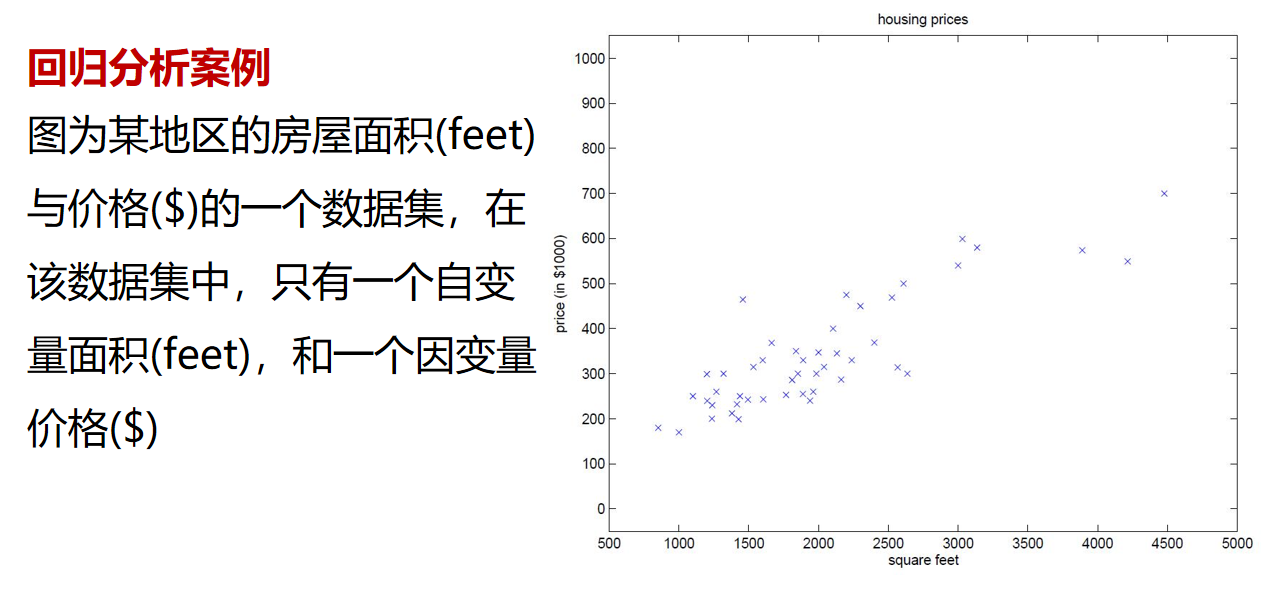
回归分析简介

回归分析最早是由19世纪末期高尔顿发展的。1855年，他发表了一篇文章名为“遗传的身高向平均数方向的回归”，分析父母与其孩子之间身高的关系，发现父母的身高越高的其孩子也越高，反之则越矮。他把孩子跟父母身高这种现象拟合成一种线性关系
但是他还发现个有趣的现象，高个子的人生出来的孩子往往比他父亲矮一点更趋于父母的平均身高，矮个子的人生出来的孩子通常比他父亲高一点也趋向于平均身高。高尔顿选用了“回归”一词，把这一现象叫做“向平均数方向的回归”

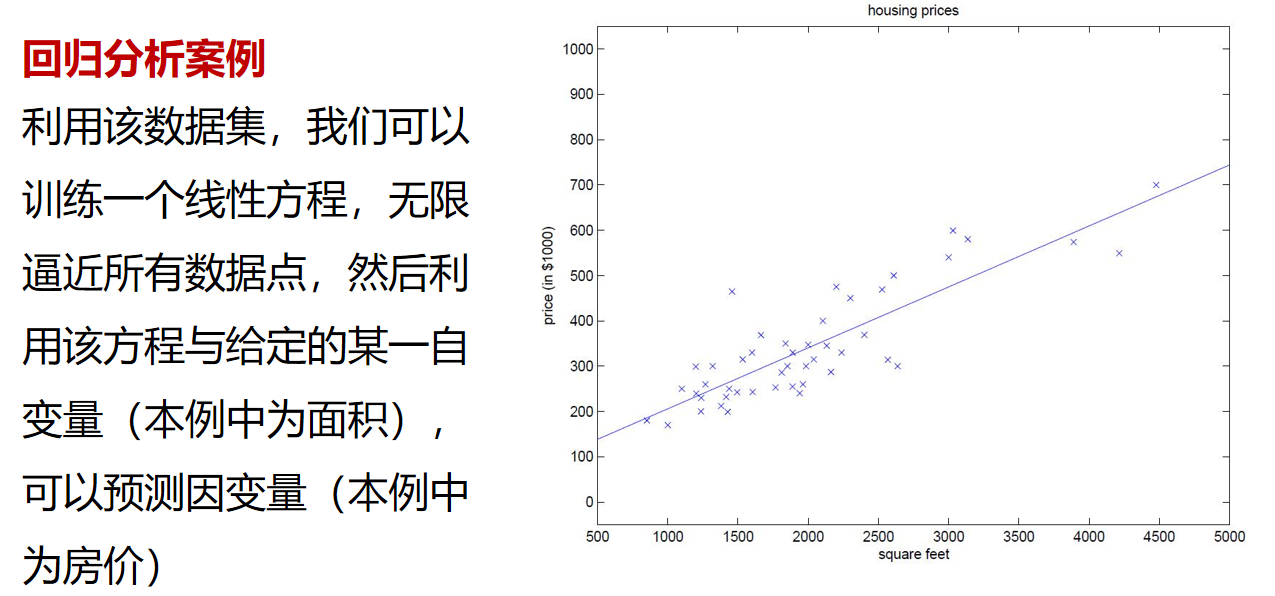
在这里插入图片描述

线性回归

在这里插入图片描述

线性回归案例：

import numpy as np
import matplotlib.pyplot as plt 
from bz2 import __author__
#设置随机种子 
seed = np.random.seed(100)
#构造一个100行1列到矩阵。矩阵数值生成用rand，得到到数字是0-1到均匀分布到小数。 
X = 2 * np.random.rand(100,1) #最终得到到是0-2均匀分布到小数组成到100行1列到矩阵。这一步构建列    X1(训练集数据) 
#构建y和x的关系。 np.random.randn(100,1)是构建的符合高斯分布（正态分布）的100行一列的随机数。相当于给每个y增加列一个波动值。 
y= 4 + 3 * X + np.random.randn(100,1)
#将两个矩阵组合成一个矩阵。得到的X_b是100行2列的矩阵。其中第一列全都是1. 
X_b = np.c_[np.ones((100,1)),X]
#解析解求theta到最优解 
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
# 生成两个新的数据点,得到的是两个x1的值 
X_new = np.array([[0],[2]])
# 填充x0的值，两个1 
X_new_b = np.c_[(np.ones((2,1))),X_new]
# 用求得的theata和构建的预测点X_new_b相乘，得到yhat 
y_predice = X_new_b.dot(theta_best)
# 画出预测函数的图像，r-表示为用红色的线 
plt.plot(X_new,y_predice,'r-')
# 画出已知数据X和掺杂了误差的y，用蓝色的点表示 
plt.plot(X,y,'b.')
# 建立坐标轴 
plt.axis([0,2,0,15,])
plt.show()

输出为：
在这里插入图片描述

from sklearn import datasets
from sklearn.linear_model import LinearRegression
data = datasets.load_boston()
linear_model = LinearRegression()
linear_model.fit(data.data,data.target)
linear_model. coef_    #获取模型自变量系数
linear_model.intercept_   #获取模型

输出如下:
在这里插入图片描述

d:\ProgramData\Anaconda3\lib\site-packages\sklearn\utils\deprecation.py:87: FutureWarning: Function load_boston is deprecated; load_boston is deprecated in 1.0 and will be removed in 1.2.

The Boston housing prices dataset has an ethical problem. You can refer to
the documentation of this function for further details.

The scikit-learn maintainers therefore strongly discourage the use of this
dataset unless the purpose of the code is to study and educate about
ethical issues in data science and machine learning.

In this special case, you can fetch the dataset from the original
source::

    import pandas as pd
    import numpy as np


    data_url = "http://lib.stat.cmu.edu/datasets/boston"
    raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
    data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
    target = raw_df.values[1::2, 2]

Alternative datasets include the California housing dataset (i.e.
:func:`~sklearn.datasets.fetch_california_housing`) and the Ames housing
dataset. You can load the datasets as follows::

    from sklearn.datasets import fetch_california_housing
    housing = fetch_california_housing()

for the California housing dataset and::

    from sklearn.datasets import fetch_openml
    housing = fetch_openml(name="house_prices", as_frame=True)

for the Ames housing dataset.

warnings.warn(msg, category=FutureWarning)

from sklearn.metrics import mean_squared_error
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

data = datasets.load_boston()
x = data.data
y = data.target
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1)
linear_model = LinearRegression()
linear_model.fit(x_train,y_train)
y_predict = linear_model.predict(x_test)
mean_squared_error(y_test,y_predict)

输出为：
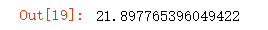
在这里插入图片描述

多项式回归

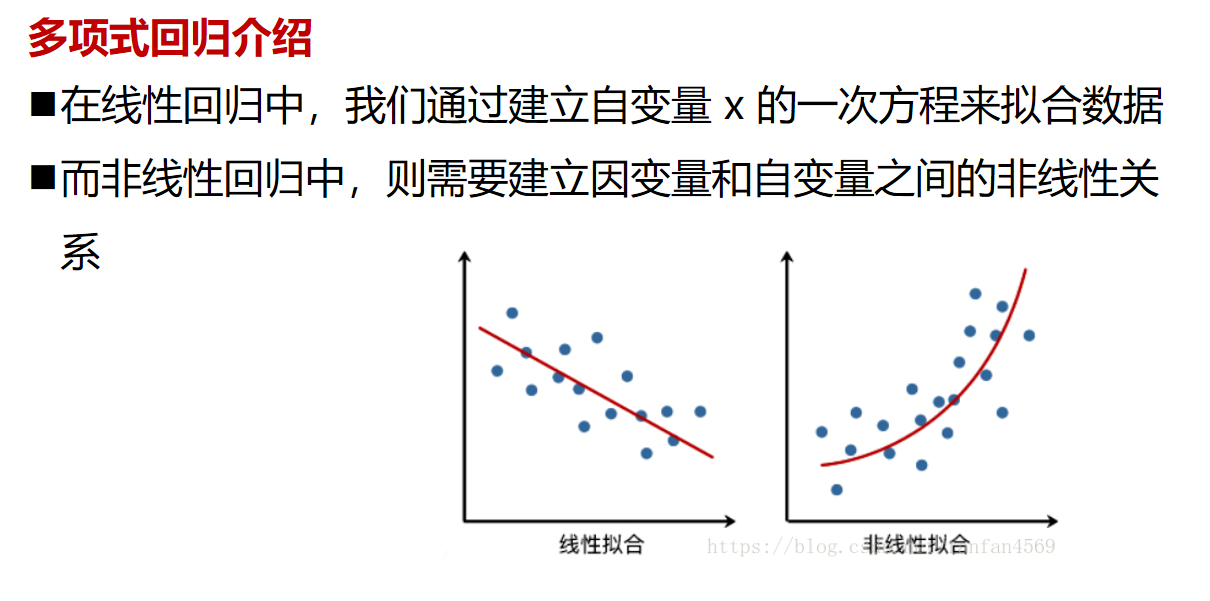
在这里插入图片描述

在 sklearn你得到多项式回归:
使用 sklearn.preprocessing.PolynomialFeatures 在原始数据集上生成多项式和交互特征
使用 sklearn.linear_model.LinearRegression 在转换后的数据集上运行普通最小二乘线性回归

from sklearn.metrics import mean_squared_error
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
# PolynomialFeatures方法实现 Poly多 nomial  Features方法实现
model_1  = PolynomialFeatures(degree=2)
data = datasets.load_boston()
x = data.data
y = data.target
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1)

linear_model = LinearRegression()
linear_model.fit(model_1.fit_transform(x_train),y_train)

y_predict = linear_model.predict(model_1.fit_transform(x_test))
mean_squared_error(y_test,y_predict)

输出为：
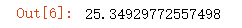
在这里插入图片描述

在这里插入图片描述

多项式回归案例

下面通过一个案例，来说明多项式回归，参考：
机器学习入门（七）：多项式回归, PolynomialFeatures详解
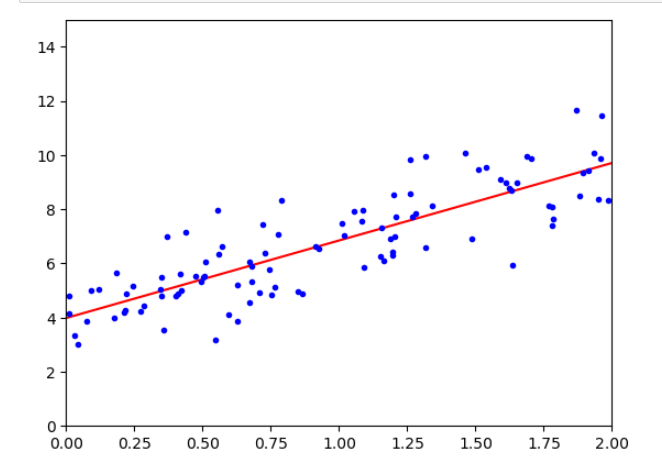
首先创建数据并且添加噪音:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
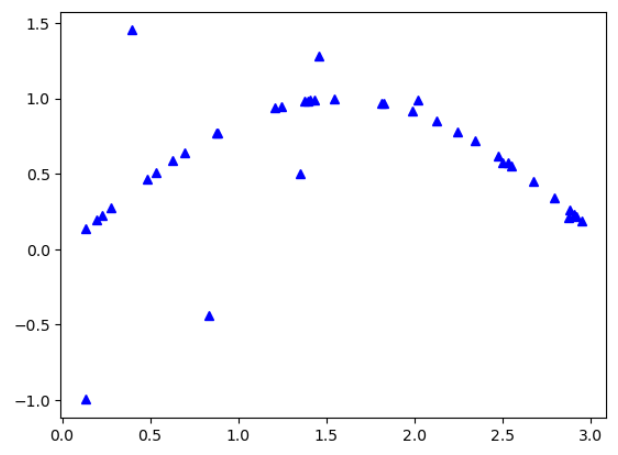
X = np.sort(3 * np.random.rand(40, 1), axis=0)  
y = np.sin(X).ravel()   
# 噪音
y[::5] += 2.5 * (0.5 - np.random.rand(8)) 
plt.plot(X,y,'b^')
plt.show()

输出为
在这里插入图片描述

然后实现多项式矩阵,并且训练模型,查看训练出来的系数w和截距b:

lr = LinearRegression()
pf=PolynomialFeatures(degree=2)
lr.fit(pf.fit_transform(X), y)
print(lr.coef_)
print(lr.intercept_)

输出为：
在这里插入图片描述

正好三个系数，分别对应常数项，一次项，二次项。
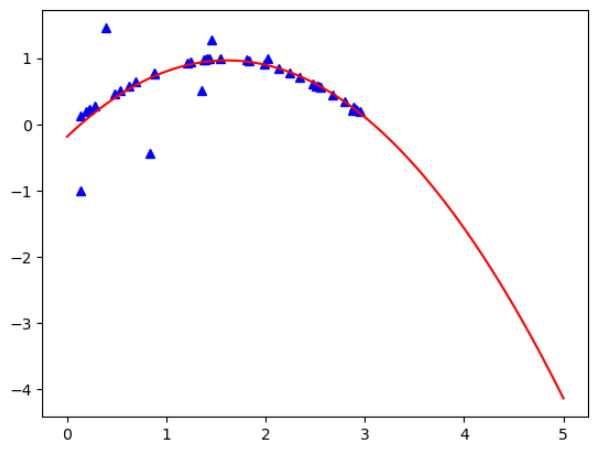
然后绘制图像：

xx = np.linspace(0, 5, 100) #生成密集点
xx2 = pf.transform(xx[:, np.newaxis]) #转换格式

yy2 = lr.predict(xx2)
plt.plot(X,y,'b^')
plt.plot(xx ,yy2,c='r')

输出为：
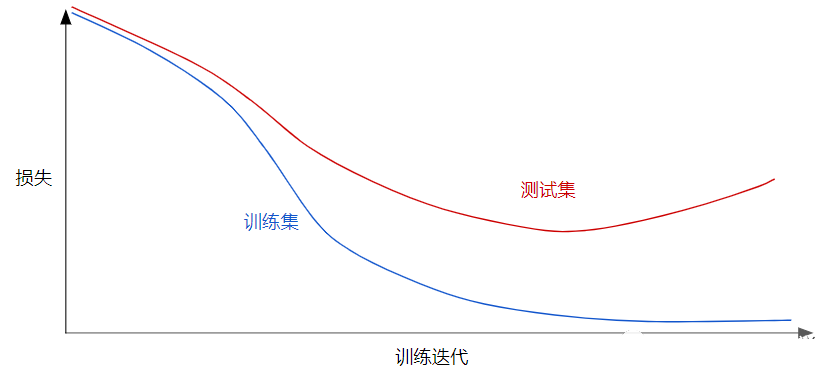
在这里插入图片描述

过拟合问题与正则化

过拟合

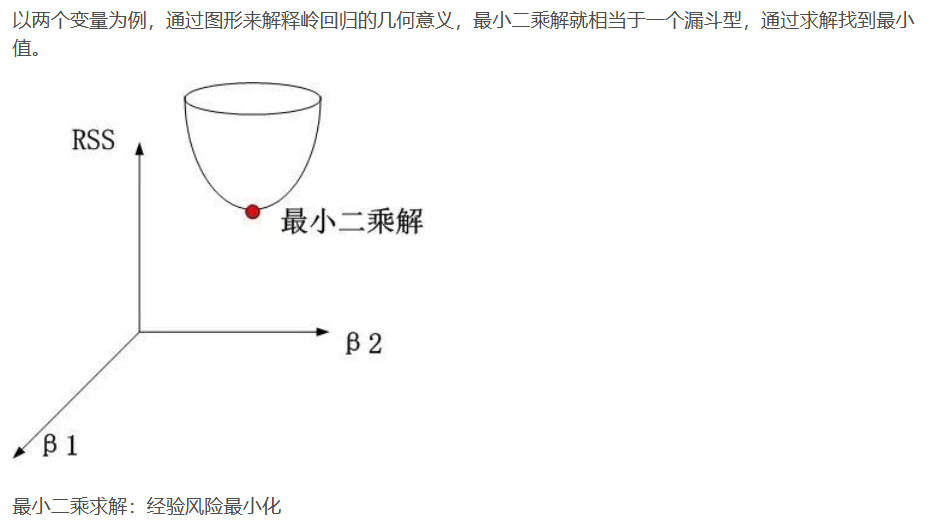
在这里插入图片描述

对于一组给定的数据，我们需要通过机器学习算法去拟合得到一个模型（对应图中曲线）。根据我们对拟合的控制和调整，这个模型可以有无数多种（一条直线，或各种形状的曲线等）。这么多种当中，哪一种是我们想要的最优结果呢？哪一种最好呢？

正则化

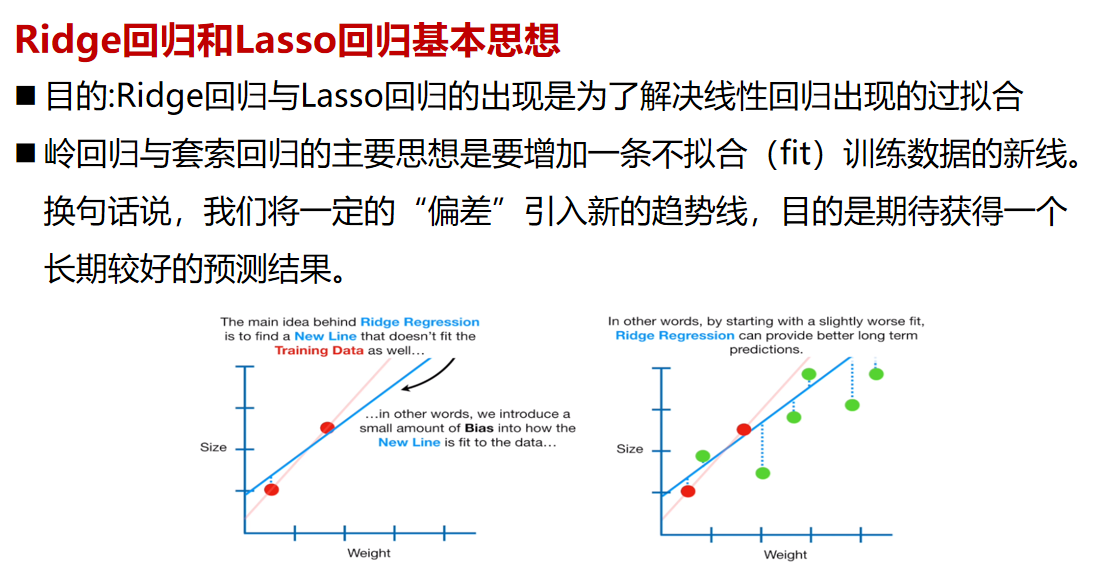
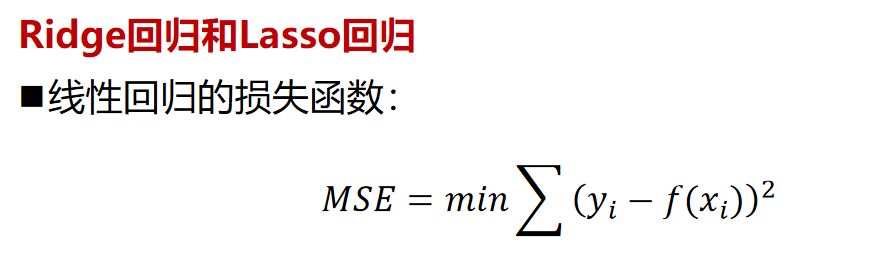
在这里插入图片描述

Ridge岭回归和Lasso回归

L2正则化 Ridge岭回归

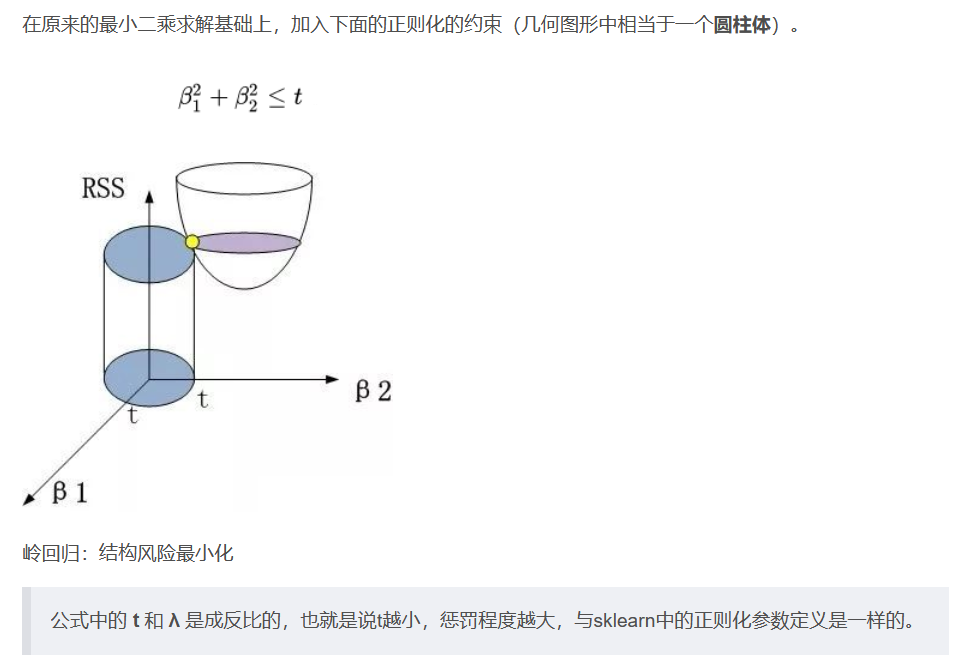
在这里插入图片描述

L1正则化：LASSO回归

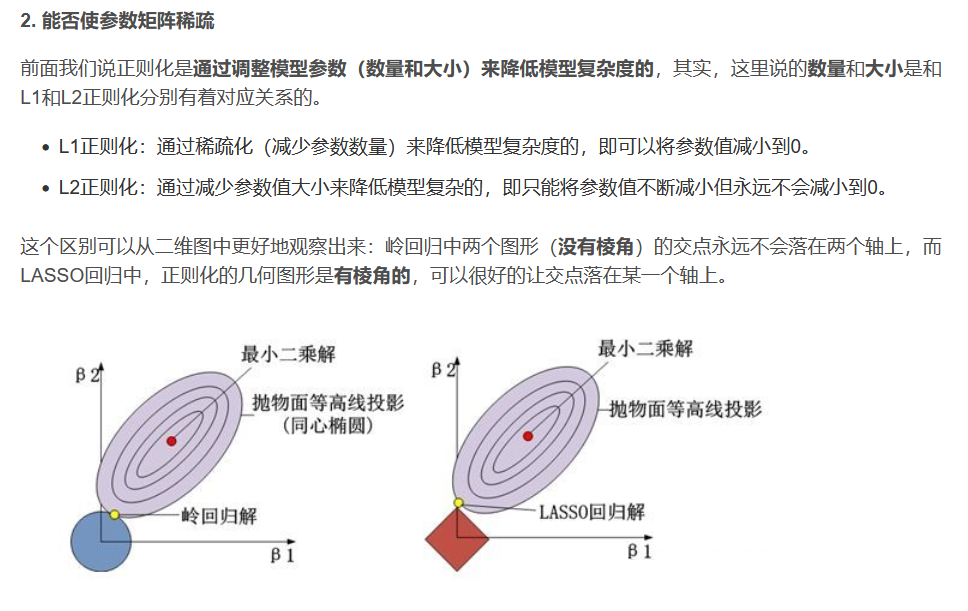
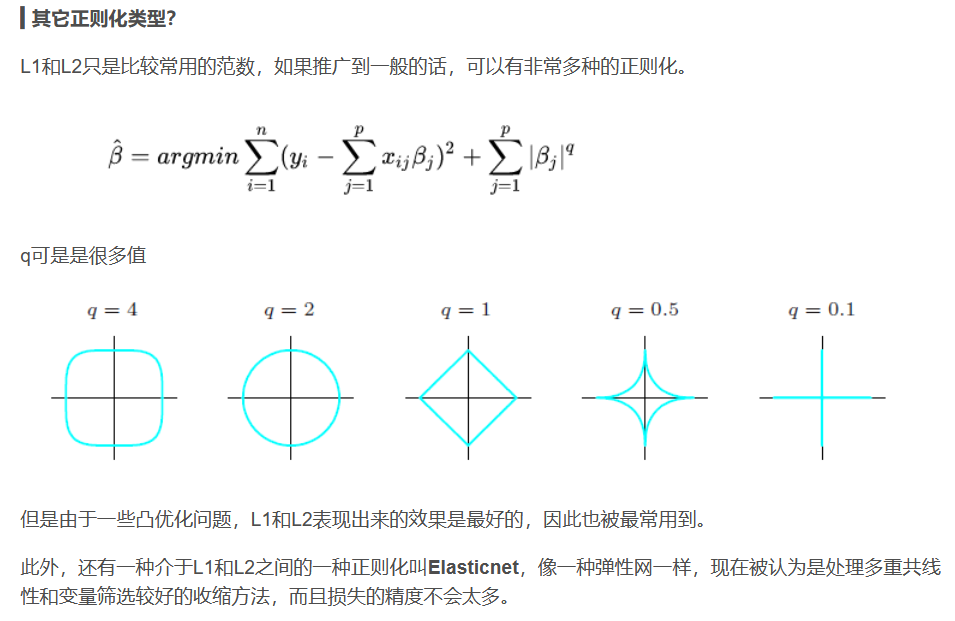
在这里插入图片描述

Ridge回归，即添加了L2正则化的线性回归；
Lasso，即添加了L1正则化的线性回归。
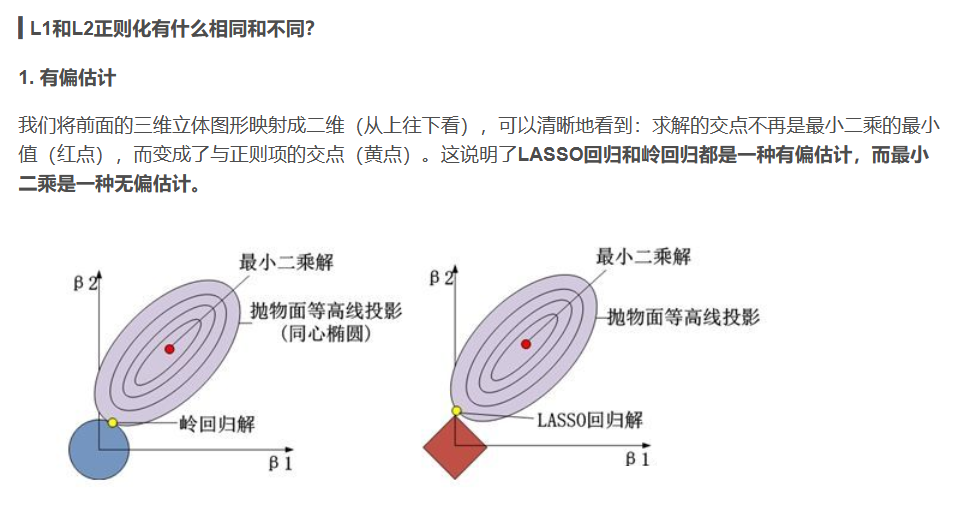
L1和L2正则化的目的都是使模型系数尽可能小，从而解决模型的过拟合问题。
他们的区别在于，l1正则化限制模型系数的l1范数尽可能小；
l2正则化限制模型系数的l2范数尽可能小。
即，Lasso回归会趋向于产生少量的特征，而其他的特征都是0，
而Ridge回归会选择更多的特征，这些特征都会接近于0。

岭回归案例

from sklearn import linear_model
from sklearn.metrics import mean_squared_error
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

data = datasets.load_boston()
x = data.data
y = data.target
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1)
# linear_model 训练
model_1 = LinearRegression()
model_1.fit(x_train,y_train)
y_predict = model_1.predict(x_test)
print("model_1\n",mean_squared_error(y_test,y_predict))
print("model_1.coef_ \n",model_1.coef_)

# redge岭回归
reg = linear_model.Ridge (alpha = .5)
reg.fit(x_train,y_train)
y_predict = reg.predict(x_test)
print("reg\n",mean_squared_error(y_test,y_predict))
print("reg.coef_ \n",reg.coef_)

在这里插入图片描述

Lasso回归案例

from sklearn import linear_model
from sklearn.metrics import mean_squared_error
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

data = datasets.load_boston()
x = data.data
y = data.target
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1)
# linear_model 训练
model_1 = LinearRegression()
model_1.fit(x_train,y_train)
y_predict = model_1.predict(x_test)
print("model_1\n",mean_squared_error(y_test,y_predict),"\n")
print("model_1.coef_ \n",model_1.coef_,"\n")


# redge岭回归
reg = linear_model.Ridge (alpha = .5)
reg.fit(x_train,y_train)
y_predict = reg.predict(x_test)
print("reg\n",mean_squared_error(y_test,y_predict),"\n")
print("reg.coef_ \n",reg.coef_,"\n")
# ========Lasso回归========
model = linear_model.Lasso(alpha=0.01)  # 调节alpha可以实现对拟合的程度
# model = linear_model.LassoCV()  # LassoCV自动调节alpha可以实现选择最佳的alpha。
# model = linear_model.LassoLarsCV()  # LassoLarsCV自动调节alpha可以实现选择最佳的alpha


model.fit(x_train,y_train)
y_predict = model.predict(x_test)
print("lasso \n",mean_squared_error(y_test,y_predict),"\n")
print("lasso.coef_ \n",model.coef_,"\n")

输出为：
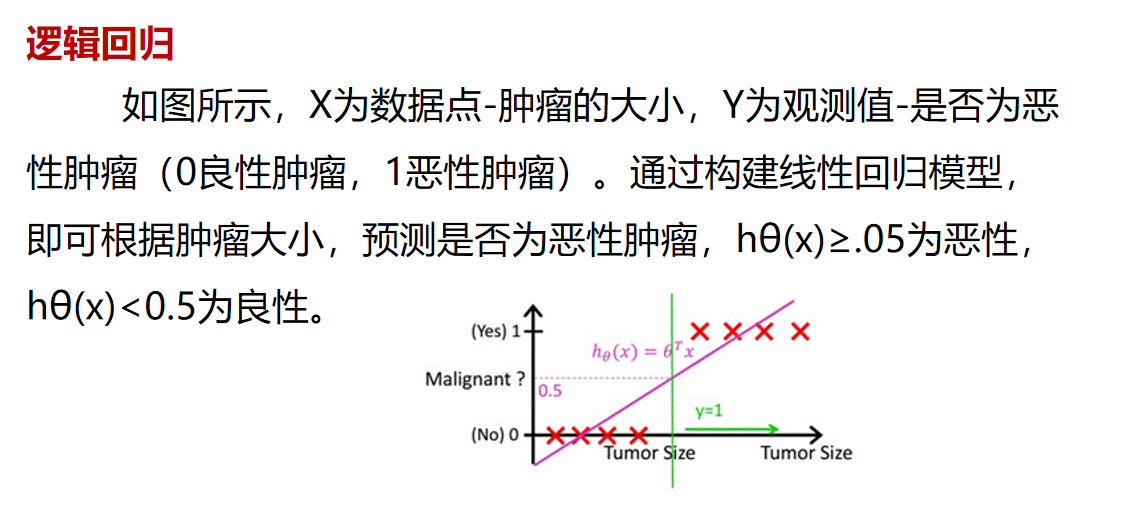
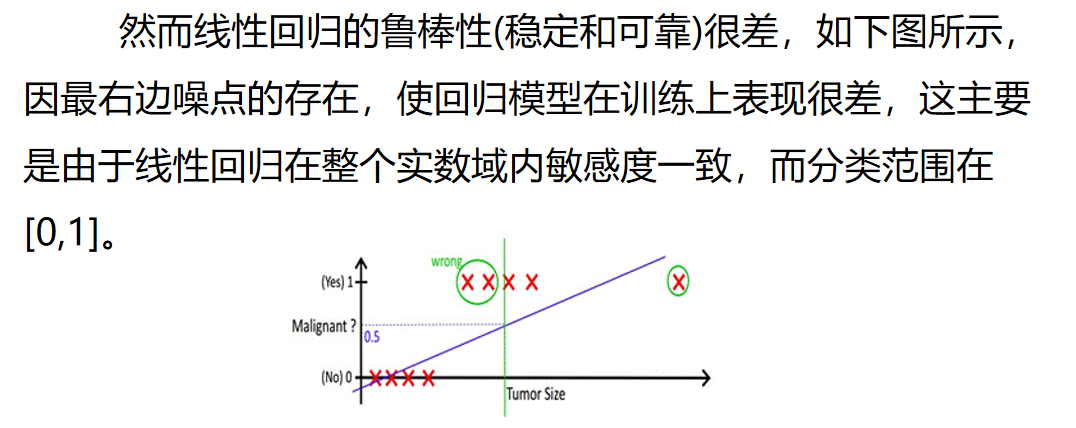
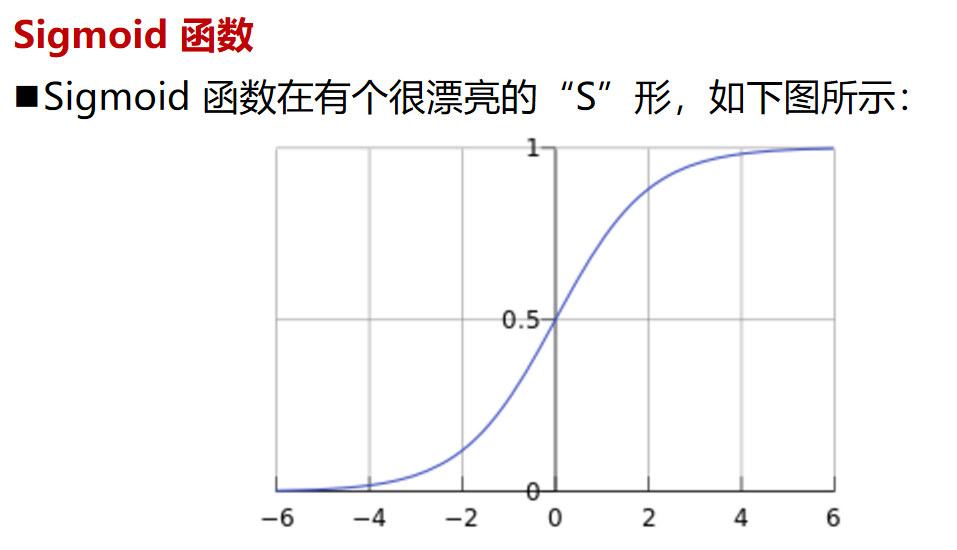
在这里插入图片描述

逻辑回归

在这里插入图片描述

逻辑回归案例

#导入数值计算的基础库
import numpy as np 
## 导入画图库
import matplotlib.pyplot as plt
import seaborn as sns
## 导入逻辑回归模型函数
from sklearn.linear_model import LogisticRegression


#利用numpy随意构造我们想要的数据集及其标签
x_fearures = np.array([[-1, -2], [-2, -1], [-3, -2], [1, 3], [2, 1], [3, 2]])
y_label = np.array([0, 0, 0, 1, 1, 1])



# 调用逻辑回归模型
lr_clf = LogisticRegression()
# 用逻辑回归模型拟合构造的数据集
lr_clf = lr_clf.fit(x_fearures, y_label) #其拟合方程为 y=w0+w1*x1+w2*x2



# 生成两个新的样本
x_fearures_new1 = np.array([[0, -1]])
x_fearures_new2 = np.array([[1, 2]])
# 利用在训练集上训练好的模型进行预测
y_label_new1_predict = lr_clf.predict(x_fearures_new1)
y_label_new2_predict = lr_clf.predict(x_fearures_new2)
# 打印预测结果
print('The New point 1 predict class:\n',y_label_new1_predict)
print('The New point 2 predict class:\n',y_label_new2_predict)

# 由于逻辑回归模型是概率预测模型,所有我们可以利用 predict_proba 函数预测其概率
# predict_proba 函数可以预测样本属于每一类的概率值
y_label_new1_predict_proba = lr_clf.predict_proba(x_fearures_new1)
y_label_new2_predict_proba = lr_clf.predict_proba(x_fearures_new2)

print('The New point 1 predict Probability of each class:\n',y_label_new1_predict_proba)
print('The New point 2 predict Probability of each class:\n',y_label_new2_predict_proba)

# The New point 1 predict class:
# [0]
# The New point 2 predict class:
# [1]
# The New point 1 predict Probability of each class:
# [[0.69567724 0.30432276]]
# The New point 2 predict Probability of each class:
# [[0.11983936 0.88016064]]


# 查看其对应模型的w（各项的系数）
print('the weight of Logistic Regression:',lr_clf.coef_)
# 查看其对应模型的w0(截距)
print('the intercept(w0) of Logistic Regression:',lr_clf.intercept_)

# the weight of Logistic Regression: [[0.73455784 0.69539712]]
# the intercept(w0) of Logistic Regression: [-0.13139986]

输出为：
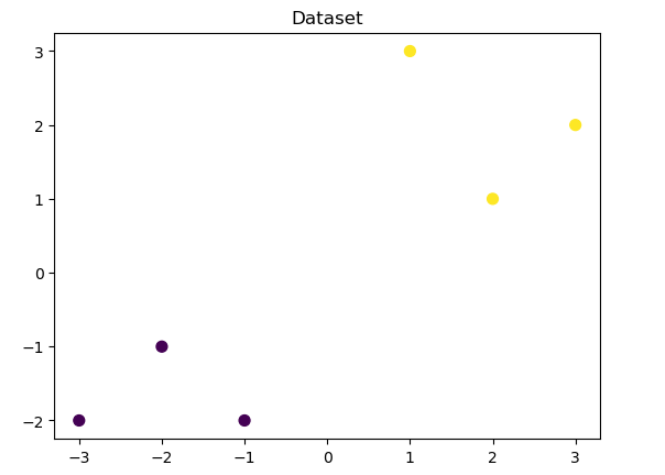
在这里插入图片描述

## 可视化构造的训练数据
plt.figure()
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')
plt.title('Dataset')
plt.show()

输出为：
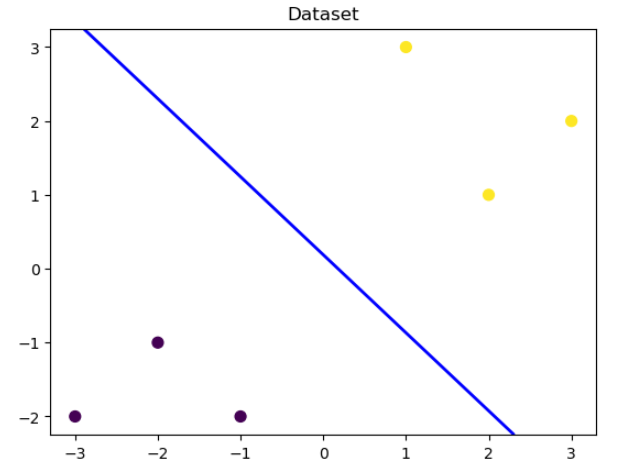
在这里插入图片描述

# 可视化决策边界

# 先可视化训练数据
plt.figure()
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')
plt.title('Dataset')

# 将上面绘制的训练数据的图像，在x轴范围内等距均分为200点，y轴范围内等距均分为100个点，
# 就相当于在绘制的图像上划分了间隔相等的20000个点（100行，200列）
nx, ny = 200, 100
x_min, x_max = plt.xlim()
y_min, y_max = plt.ylim()
x_grid, y_grid = np.meshgrid(np.linspace(x_min, x_max, nx),np.linspace(y_min, y_max, ny))
# 并分别预测这20000个点y=1的概率，并设置绘制轮廓线的位置为0.5（即y=0.5处，绘制等高线高度），并设置线宽为2，
# 颜色为蓝色（图中蓝色线即为决策边界），当然我们也可以将将0.5设置为其他的值，更换绘制等高线的位置，
# 同时也可以设置一组0~1单调递增的值，绘制多个不同位置的等高线
# 也可以理解为，此时我们将0.5设置为阈值，当p>0.5时，y=1；p<0.5时，y=0，蓝色线就是分界线
z_proba = lr_clf.predict_proba(np.c_[x_grid.ravel(), y_grid.ravel()])
z_proba = z_proba[:, 1].reshape(x_grid.shape)
plt.contour(x_grid, y_grid, z_proba, [0.5], linewidths=2., colors='blue')

plt.show()

输出为：
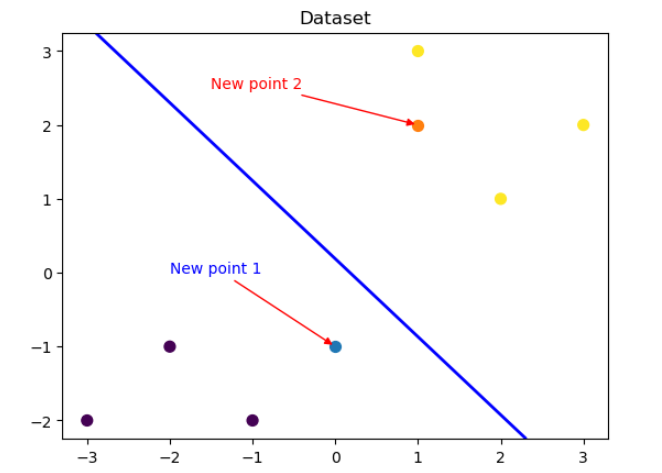
在这里插入图片描述

# 可视化测试数据
plt.figure()
# 可视化测试数据1， 并进行相应的文字注释
x_fearures_new1 = np.array([[0, -1]])
plt.scatter(x_fearures_new1[:,0],x_fearures_new1[:,1], s=50, cmap='viridis')
plt.annotate(text='New point 1',xy=(0,-1),xytext=(-2,0),color='blue',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))

# 可视化测试数据2， 并进行相应的文字注释
x_fearures_new2 = np.array([[1, 2]])
plt.scatter(x_fearures_new2[:,0],x_fearures_new2[:,1], s=50, cmap='viridis')
plt.annotate(text='New point 2',xy=(1,2),xytext=(-1.5,2.5),color='red',arrowprops=dict(arrowstyle='-|>',connectionstyle='arc3',color='red'))

# 可视化训练数据
plt.scatter(x_fearures[:,0],x_fearures[:,1], c=y_label, s=50, cmap='viridis')
plt.title('Dataset')

# 可视化决策边界
plt.contour(x_grid, y_grid, z_proba, [0.5], linewidths=2., colors='blue')

plt.show()