【算法竞赛进阶指南】0x05 排序

news2024/11/16 17:58:43

0x05排序

排序基本算法

785. 快速排序 - AcWing题库姑且用这个评测。

1.选择、插入、冒泡

这类排序是基于比较的排序算法，时间复杂度为O\left ( n^{2} \right )

选择排序

思路比较简单，就是每一次从后面选出最小的数字来与当前这个数字交换

#include<bits/stdc++.h>
const int N=1e6+10;
int n,a[N];
void select_sort()
{
    for(int i=1;i<=n;i++)
    {
        int minn=a[i];
        int sign=i;
        for(int j=i;j<=n;j++)
        {
            if(a[j]<minn)
            {
                minn=a[j];
                sign=j;
            }
        }
        std::swap(a[i],a[sign]);
    }
}
signed main()
{
    std::cin>>n;
    for(int i=1;i<=n;i++) std::cin>>a[i];
    select_sort();
    for(int i=1;i<=n;i++) std::cout<<a[i]<<" ";
    return 0;
}

插入排序

排序算法——直接插入排序（图文超详细！）-CSDN博客

思路就是每次对当前的数字找到前面第一个大于等于它的j，否则就往后移。

#include<bits/stdc++.h>
const int N=1e6+10;
int n,a[N];
void insert_sort()
{
    int j;
    for(int i=2;i<=n;i++)
    {
        if(a[i]<a[i-1])
        {
            int t=a[i];
            for(j=i-1;j>=1&&t<a[j];j--)
            {//在第一个t>=a[j]的位置退出
                a[j+1]=a[j];
            }
            a[j+1]=t;
        }
    }
}
signed main()
{
    std::cin>>n;
    for(int i=1;i<=n;i++) std::cin>>a[i];
    insert_sort();
    for(int i=1;i<=n;i++) std::cout<<a[i]<<" ";
    return 0;
}
冒泡排序

冒泡排序-排序-CSDN博客

看里面的动图就很好理解了，从左到右对每两个相邻的数都比较一次，那么到一轮之后最大的数就会跑到最后一个，这样重复n轮就可以实现排序的功能。

#include<bits/stdc++.h>
const int N=1e6+10;
int n,a[N];
void pop_sort()
{
    for(int i=1;i<=n;i++)//走的次数
    {
        for(int j=1;j<=n-i;j++)
        {
            if(a[j]>a[j+1])
            {
                std::swap(a[j],a[j+1]);
            }
        }
    }
}
signed main()
{
    std::cin>>n;
    for(int i=1;i<=n;i++) std::cin>>a[i];
    pop_sort();
    for(int i=1;i<=n;i++) std::cout<<a[i]<<" ";
    return 0;
}

2.堆排序、归并排序、快速排序

也是基于比较的排序算法，时间复杂度为O\left ( nlogn \right )

基于比较的排序算法的时间复杂度下界为 O\left ( nlogn \right )，这已经是时间复杂度最优的基于比较的排序算法。

堆排序 

【算法】排序算法之堆排序 - 知乎 (zhihu.com)

归并排序

787. 归并排序 - AcWing题库

先排序再合并

#include<bits/stdc++.h>
const int N=1e6+10;
int a[N],b[N];
void hebin(int l,int r)
{
	int mid=l+r>>1;
	int p=l,q=mid+1;
	for(int i=l;i<=r;i++)
	{
		if((p<mid+1&&a[p]<=a[q]) || q>r)
		{
			b[i]=a[p++];
		}else b[i]=a[q++]; 
	}
	for(int i=l;i<=r;i++) 
		a[i]=b[i];
}
void merge_sort(int l,int r)
{
	int mid=l+r>>1;
	if(l==r) return ;
	merge_sort(l,mid);
	merge_sort(mid+1,r);
	
	hebin(l,r);	
} 
signed main()
{
	int n;
	std::cin>>n;
	for(int i=1;i<=n;i++)
	{
		std::cin>>a[i];
	}
	merge_sort(1,n);
	for(int i=1;i<=n;i++)
		std::cout<<a[i]<<" ";
	return 0;
}
快速排序

785. 快速排序 - AcWing题库

随便从区间里选择一个点，让左边的数都比他小，右边的数都比它大。

#include<bits/stdc++.h>
const int N=1e6+10;
int n,a[N];
void quick_sort(int l,int r)
{
    if(l>=r) return ;
    int x=a[l+r>>1];
    int i=l-1,j=r+1;
    while(i<j)
    {
        do i++;while(a[i]<x);
        do j--;while(a[j]>x);
        if(i<j) std::swap(a[i],a[j]);
    }
    
    quick_sort(l,j);
    quick_sort(j+1,r);
    
}
signed main()
{
    std::cin>>n;
    for(int i=1;i<=n;i++) std::cin>>a[i];
    
    quick_sort(1,n);
    
    for(int i=1;i<=n;i++) std::cout<<a[i]<<" ";
    return 0;
}

 3.计数排序、基数排序、桶排序

计数排序

【算法】排序算法之计数排序 - 知乎 (zhihu.com)

基数排序

最详细的【基数排序】---排序算法，思路清晰动图保姆级讲解，五分钟搞懂！_csdn基数排序动图-CSDN博客

桶排序

【算法】排序算法之桶排序 - 知乎 (zhihu.com)

排序算法应用

离散化

排序算法的第一个应用是离散化。就是把无穷大集合中的若干个元素映射为有限集合以便于统计的方法。如：问题范围很大但只涉及其中m个数，并且与数值的绝对大小无关，我们就可以把这m个数字与1-m建立映射关系。

void discrete()//离散化
{
	std::sort(a+1,a+1+n);
	//去重 
	for(int i=1;i<=n;i++)
	{
		if(i==1||a[i]!=a[i-1])
		{
			b[++m]=a[i];
		}
	}
} 
int query(int x)//查询x的映射 
{
	return std::lower_bound(b+1,b+m+1,x)-b; 
}

关于lower_bound( )和upper_bound( )的常见用法_lowerbound和upperbound-CSDN博客

简单概括一下就是lower_bound找到第一个<=num的值，upper返回第一个>。这两个函数都是返回一个迭代器，减去初始位置就可以得到下标。

同时在函数参数中加上greater<int>()就把上面的<改成了>。

103. 电影 - AcWing题库

e这题就是给定n个编号，从m个里面发现人数最大的解就可以。其实只需要开个map记录每种语言有多少人会就行了，毕竟没人关心谁会谁不会。循环里维护sign即可。

#include<bits/stdc++.h>
using ll=long long;
//#define int ll
const int N=2e5+10;
int n,m,k;
int a,b[N],c[N];
std::map<int,int> mp;//记录懂这个语言的人的个数 

void solve()
{
	std::cin>>n;
	for(int i=1;i<=n;i++)
	{
		std::cin>>a;	
		mp[a]++;
		//std::cout<<a<<" "<<mp[a]<<'\n';
	}	
	
	std::cin>>m;
	int maxn=0,sign=m,maxnn=0;
	for(int i=1;i<=m;i++)
	{
		std::cin>>b[i];
	}
	for(int i=1;i<=m;i++)
	{
		std::cin>>c[i];
		
		int now=mp[b[i]];
		if(now>maxn)
		{
			//std::cout<<i<<'\n';
			maxn=now,sign=i;
			maxnn=mp[c[i]];
			
		}else if(now==maxn){
			if(mp[c[i]]>maxnn)
			{
				maxnn=mp[c[i]];
				sign=i;
			}
		}	
	}
	std::cout<<sign<<'\n';
}
signed main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    int t=1;
	//std::cin>>t;
    while(t--)
    {
        solve();
    }
    return 0;
}

中位数

104. 货仓选址 - AcWing题库

需要某家店到所有店的距离之和最短，奇数时最中间那个点最短，偶数时中间两个点都行。

#include<bits/stdc++.h>
using ll=long long;
//#define int ll
const int N=2e5+10;
int n,m,k;
int a[N];
ll ans;
void solve()
{
	std::cin>>n;
	for(int i=1;i<=n;i++)
	{
		std::cin>>a[i];	
	}	
	std::sort(a+1,1+a+n);
	
	for(int i=1;i<=n;i++)
	{
		ans+=std::abs(a[i]-a[n/2+1]);
	} 
	std::cout<<ans;
}
signed main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    int t=1;
	//std::cin>>t;
    while(t--)
    {
        solve();
    }
    return 0;
}
105. 七夕祭 - AcWing题库

专门开了个博客写这个问题，会详细点。 

【算法】环形纸牌均分问题-CSDN博客

#include<bits/stdc++.h>
using ll=long long;
const int N=1e5+10;
const int mod=1e9+7;
int row[N],col[N],sr[N],sl[N];
int n,m,s;
ll cnt1=-1,cnt2=-1;
void solve()
{
	std::cin>>n>>m>>s;
	for(int i=1;i<=s;i++)
	{
		int x,y;
		std::cin>>x>>y;
		row[x]++,col[y]++;
	}
	if(s%n==0)//对行 
	{
		cnt1=0;
		int t=s/n;
		for(int i=1;i<=n;i++)
		{
			row[i]-=t;
			sr[i]=sr[i-1]+row[i];	
		}  
		std::sort(sr+1,sr+1+n);
		int mid=1+n/2;
		for(int i=1;i<=n;i++)
		{
			cnt1+=std::abs(sr[i]-sr[mid]);
		}
	}
	if(s%m==0)//对列
	{
		cnt2=0;
		int t=s/m;
		for(int i=1;i<=m;i++)
		{
			col[i]-=t;
			sl[i]=sl[i-1]+col[i];	
		}  
		std::sort(sl+1,sl+1+m);
		int mid=1+m/2;
		for(int i=1;i<=m;i++)
		{
			cnt2+=std::abs(sl[i]-sl[mid]);
		}
	}
	if(cnt1==-1&&cnt2==-1)
	{
		std::cout<<"impossible"<<'\n';
	}else{
		if(cnt1!=-1&&cnt2!=-1)
		{
			std::cout<<"both"<<' ';
			std::cout<<cnt1+cnt2<<'\n';
		}else if(cnt1!=-1){
			std::cout<<"row"<<' ';
			std::cout<<cnt1<<'\n';
		}else{
			std::cout<<"column"<<' ';
			std::cout<<cnt2<<'\n';
		}
	}
}
signed main()
{
    std::ios::sync_with_stdio(false);
    std::cin.tie(0);
    int t=1;
	//std::cin>>t;
    while(t--)
    {
        solve();
    }
    return 0;
}
106. 动态中位数 - AcWing题库

依次读入一个整数序列，每当已经读入的个数为奇数时，输出已读入的序列的中位数。

对数组排序的时间复杂度是nlogn，但是求解中位数实际上并不要求这个数组有序。我们只需要找到一个数字，左边一半都比他小，右边一半都比他大。

如何让左边一半都比它小，右边一半都比他大呢？我们可以建两个堆，左边一个大根堆，右边一个小根堆。是不是只要大根堆所有元素都比小根堆的所有元素小，并且数量满足一定关系就好了？

我们假定中位数，n/2+1是大根堆的堆顶，那么左边有n/2+1个元素，右边有n/2个元素。那么需要满足的数量关系是不是就是，leftsize-1==rightsize。

因此，进来一个数我们就把他放进大根堆。如果，大根堆的top比小根堆的top还大了，我们只需要交换两个top即可，这样我们就维护了左边的始终小于右边的。

在堆稳定之后，我们就要判断左边堆的数量是不是太多了。如果是就弹出top并放入right即可。

#include<bits/stdc++.h>
using ll=long long;
const int N=1e4+10;
int a[N];
void solve()
{
    int sno,n;
    std::cin>>sno>>n;

    std::cout<<sno<<" "<<n/2+1<<'\n';
    std::priority_queue<int> left;//大根堆
    std::priority_queue<int,std::vector<int>,std::greater<int>> right;

    int cnt=0;
    for(int i=1;i<=n;i++)
    {
        int x;
        std::cin>>x;

        left.push(x);
        if(!right.empty()&&left.top()>right.top())
        {
            int a=left.top(),b=right.top();
            left.pop(),right.pop();
            right.push(a),left.push(b);
        }

        //左边n/2+1，右边n/2
        if(left.size()-1>right.size())//左边太多了
        {
            right.push(left.top());
            left.pop();
        }

        if(i%2)
        {
            cnt++;
            std::cout<<left.top()<<" ";
            if(cnt%10==0) std::cout<<'\n';//达到十个就回车
        }
    }
    if(cnt%10) std::cout<<'\n';
}
signed main()
{
    int t=1;
    std::cin>>t;
    while(t--)
    {
        solve();
    }
    return 0;
}

第k大数

786. 第k个数 - AcWing题库

这个也可以用上面的对顶堆来做，只需要把大小条件改了就行。每次进堆之前比较，如果当前数比lefttop大就丢到右边，否则把lefttop抛出，把这个数塞进去。

#include<bits/stdc++.h>
using ll=long long;
const int N=1e5+10;
int x;
int n,k;
void solve()
{
    std::priority_queue<int> left;
	std::priority_queue<int,std::vector<int>,std::greater<int>> right;
	std::cin>>n>>k;
	for(int i=1;i<=n;i++)
	{
		std::cin>>x;
		
	    left.push(x);	
		if(left.size()>k)
		{
		    right.push(left.top());
		    left.pop();
		}
		if(!right.empty()&&left.top()>right.top())
		{
		    int a=left.top(),b=right.top();
		    left.pop(),right.pop();
		    left.push(b),right.push(a);
		}
	}
	std::cout<<left.top();
}
signed main()
{
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);
	int t=1;
	//std::cin>>t;
	while(t--)
	{
		solve();
	}
	return 0;
}

还有一种做法是快速排序，快速排序的过程是每次选择一个数让左边都比他小，右边都比他大，然后再分别递归两边进行排序。然而，我们追求的不是有序的数组，我们只需要知道第k大的是什么就好，因此我们每次可以舍弃一半的区间。平均情况下时间复杂度为O(n)。

#include<bits/stdc++.h>
using ll=long long;
const int N=1e5+10;
int a[N];
int n,k;
int quick_sort(int l,int r)
{
	if(l==r) return a[l];
	int mid=l+r>>1;
	int x=a[mid];
	int i=l-1,j=r+1;
	while(i<j)
	{
		do i++;while(a[i]<x);
		do j--;while(a[j]>x);
		if(i<j) std::swap(a[i],a[j]);
	}
	if(j>=k) return quick_sort(l,j);
	else return quick_sort(j+1,r);
}
void solve()
{
	std::cin>>n>>k;
	for(int i=1;i<=n;i++)
	{
		std::cin>>a[i];
	}
	std::cout<<quick_sort(1,n);
}
signed main()
{
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);
	int t=1;
	//std::cin>>t;
	while(t--)
	{
		solve();
	}
	return 0;
}

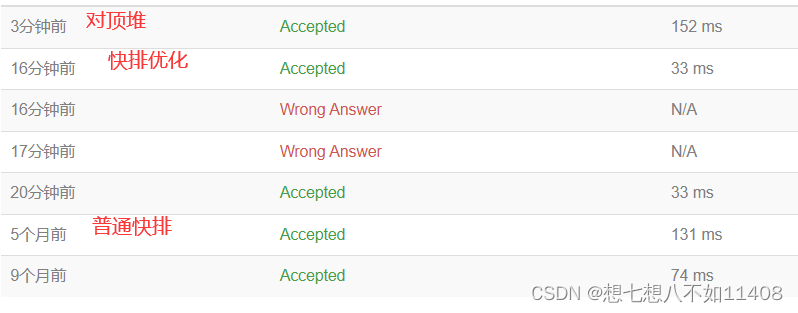
比较一下时间，还是快排优化之后的代码更加理想。

对于对顶堆这个做法主要是可以在线以O1的时间处理，如果离线处理还不如直接排序。

逆序对

对一个序列a，如果i<j 并且 a[i] >a[j]，则称a[i] 与a[j]构成逆序对。

求逆序对的常用方法是归并排序，还有树状数组（后面应该会学）。

贴个归并排序。

#include<bits/stdc++.h>
using ll=long long;
const int N=1e5+10;
int a[N],b[N];
int n,k;
void hebin(int l,int r)
{
	int mid=l+r>>1;
	int i=l,j=mid+1;
	int k=0;
	while(i<=mid&&j<=r)
	{
		if(a[i]<=a[j]) b[++k]=a[i++];
		else b[++k]=a[j++];	
	}	
	while(i<=mid) b[++k]=a[i++];
	while(j<=r) b[++k]=a[j++];
	
	for(int i=l,j=1;i<=r,j<=k;i++,j++) a[i]=b[j];
}
void merge_sort(int l,int r)
{
	if(l==r) return ;
	int mid=l+r>>1;
	merge_sort(l,mid);
	merge_sort(mid+1,r);
	
	hebin(l,r);
}
void solve()
{
	std::cin>>n;
	for(int i=1;i<=n;i++)
	{
		std::cin>>a[i];
	}
	merge_sort(1,n);
	for(int i=1;i<=n;i++)
	{
		std::cout<<a[i]<<" ";
	}
}
signed main()
{
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);
	int t=1;
	//std::cin>>t;
	while(t--)
	{
		solve();
	}
	return 0;
}

 如果要计算逆序对个数只需要加上一段代码（逆序对个数记得开long long！

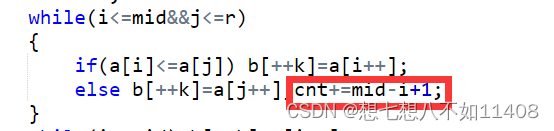
为啥是这样呢？

再合并数组里，我们合并l~mid和mid~r这两段区间，此时指针走到了i，则i~mid都会比j小，因此加上这段区间的长度mid-i+1即可。

107. 超快速排序 - AcWing题库

 确定超快速排序需要执行多少交换操作才能对给定的输入序列进行排序

把每一对逆序的交换就行了呗，实际上就是求逆序对的个数。

#include<bits/stdc++.h>
using ll=long long;
const int N=5e5+10;
int a[N],b[N];
int n,k;
ll cnt;
void hebin(int l,int r)
{
	int mid=l+r>>1;
	int i=l,j=mid+1;
	int k=0;
	while(i<=mid&&j<=r)
	{
		if(a[i]<=a[j]) b[++k]=a[i++];
		else b[++k]=a[j++],cnt+=mid-i+1;	
	}	
	while(i<=mid) b[++k]=a[i++];
	while(j<=r) b[++k]=a[j++];
	
	for(int i=l,j=1;i<=r,j<=k;i++,j++) a[i]=b[j];
}
void merge_sort(int l,int r)
{
	if(l==r) return ;
	int mid=l+r>>1;
	merge_sort(l,mid);
	merge_sort(mid+1,r);
	
	hebin(l,r);
}
void solve()
{
	std::cin>>n;
	if(n==0) return ;
	cnt=0;
	for(int i=1;i<=n;i++)
	{
		std::cin>>a[i];
	}
	merge_sort(1,n);
	
	std::cout<<cnt<<'\n';
}
signed main()
{
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);
	int t=1;
	//std::cin>>t;
	while(t)
	{
		solve();
		if(n==0) break;
	}
	return 0;
}
108. 奇数码问题 - AcWing题库

可以把棋盘抽象出来，左右交换不会改变元素的排列。因此我们只考虑上下交换，当m为奇数的时候，上下交换会_23 456 789->423 _56 789绕过2个数，这必定是偶数，也就是每次交换只改变偶数次逆序对。如果给定的两个状态的逆序对个数的奇偶性不同，那么怎么都不会成功。因此这题我们只需要判断两种状态的逆序对个数奇偶性即可。

如果n是偶数呢？每次交换绕过奇数个，但我们只会换空格行的差次。为什么？虽然我们可以来回不停的换，但来回换并不会一下逆序对的奇偶性。因此判断逆序对数之差和行数之差奇偶性是否相同即可。

参考：排序与贪心知识点小结 - a1b3c7d9 - 博客园 (cnblogs.com)

因为这题难点在于思维不在于代码，所以这里偷个懒直接cp别人代码hh。

#include <bits/stdc++.h>
using namespace std;
const int N=510;
int n,m,a[N*N],b[N*N],c[N*N],i,j,k;
long long cnt;
void merge(int a[],int l,int r)
{
    if (r-l<1)
        return ;
    int mid=(l+r)>>1;
    merge(a,l,mid);
    merge(a,mid+1,r);
    int i=l,j=mid+1;
    for (int k=l; k<=r; k++)
    {
        if (j>r || i<=mid && a[i]<=a[j])
            b[k]=a[i++];
        else
        {
            cnt+=mid-i+1;
            b[k]=a[j++];
        }
    }
    for (int k=l; k<=r; k++)
        a[k]=b[k];
}
signed main()
{
    ios::sync_with_stdio(false);
    while(cin>>n)
    {
        int ok=0,x;
        for (i=1; i<=n*n; i++)
        {
            cin>>x;
            if (x==0)
                ok=1;
            else
                a[i-ok]=x;
        }
        ok=0;
        for (i=1; i<=n*n; i++)
        {
            cin>>x;
            if (x==0)
                ok=1;
            else
                c[i-ok]=x;
        }
        cnt=0;
        memset(b,0,sizeof(b));
        merge(a,1,n*n);
        long long ans=cnt;
        memset(b,0,sizeof(b));
        cnt=0;
        merge(c,1,n*n);
        if ((ans&1)==(cnt&1))
            puts("TAK");
        else
            puts("NIE");
    }
    return 0;
}

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1542265.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

(一)基于IDEA的JAVA基础7

(一)基于IDEA的JAVA基础7

关系运算符 运算符 含义 范例 结果 等于 12 false &#xff01; 不等于 1&#xff01;2 true > 大于 1>2 false < 小于 …
阅读更多...
【协议-HTTPS】

【协议-HTTPS】

https https是在http协议的基础上&#xff0c;添加了SSL/TLS握手以及数据加密传输&#xff0c;也属于应用层协议。 httpshttp加密认证完整性保护 https交互图&#xff1a; HTTPS的整体过程分为证书验证和数据传输阶段&#xff1a; ① 证书验证阶段 浏览器发起 HTTPS 请求 服务…
阅读更多...
如何通过idea搭建一个SpringBoot的Web项目（最基础版）

如何通过idea搭建一个SpringBoot的Web项目（最基础版）

通过idea搭建一个SpringBoot的Web项目 文章目录 通过idea搭建一个SpringBoot的Web项目一、打开idea&#xff0c;找到 create new project二、创建方式三、配置项目依赖四、新建项目模块五、总结 一、打开idea&#xff0c;找到 create new project 方式1 方式2 二、创建方式 新…
阅读更多...
如何使用PHP和RabbitMQ实现消息队列？

如何使用PHP和RabbitMQ实现消息队列？

前言 今天我们来做个小试验&#xff0c;用PHP和RabbitMQ实现消息队列功能。 前期准备&#xff0c;需要安装好docker、docker-compose的运行环境。 如何使用docker部署php服务_php如何使用docker发布-CSDN博客 一、安装RabbitMQ 1、创建相关目录&#xff0c;执行如下命令。…
阅读更多...
linux 通过nvm安装node

linux 通过nvm安装node

我的博客原文&#xff1a;linux 通过nvm安装node 前言 nvm是一个node版本控制的工具&#xff0c;他可以查看可以安装的node版本&#xff0c;安装node&#xff0c;以及切换node版本&#xff0c;传统的node安装&#xff0c;我们是下载压缩包&#xff0c;然后指定环境变量&…
阅读更多...
医院预约挂号系统设计与实现|jsp+ Mysql+Java+ Tomcat(可运行源码+数据库+设计文档)

医院预约挂号系统设计与实现|jsp+ Mysql+Java+ Tomcat(可运行源码+数据库+设计文档)

本项目包含可运行源码数据库LW&#xff0c;文末可获取本项目的所有资料。 推荐阅读100套最新项目 最新ssmjava项目文档视频演示可运行源码分享 最新jspjava项目文档视频演示可运行源码分享 最新Spring Boot项目文档视频演示可运行源码分享 2024年56套包含java&#xff0c;…
阅读更多...
MySQL数据库基本操作（增删改查）与用户授权

MySQL数据库基本操作（增删改查）与用户授权

前言 SQL&#xff08;Structured Query Language&#xff0c;结构化查询语言&#xff09;是一种用于管理关系数据库系统的语言。SQL的设计目标是提供一种简单、直观的语言&#xff0c;使得用户可以通过编写SQL语句来处理他们想要的数据和操作。 目录 一、结构介绍 1. 查看信…
阅读更多...
计算机软件安全

计算机软件安全

一、软件安全涉及的范围 1.1软件本身的安全保密 软件的本质与特征&#xff1a; 可移植性 寄生性 再生性 可激发性 攻击性 破坏性 …… 知识产权与软件盗版 软件商品交易形式不透明&#xff0c;方式多样&#xff0c;传统商标标识方法不适用&#xff1b; 盗版方法简捷…
阅读更多...
Django Ajax

Django Ajax

【一】Json 【1】介绍 JSON&#xff08;javascript object otaition&#xff09;是一种轻量级的数据交换格式JSON使用了Javascript的一部分语法来定义其数据格式&#xff0c;但Json是独立于语言的Json采用完全独立于语言的文本格式&#xff0c;使得Json成为理想的数据交互语言…
阅读更多...
PCB布线和灌铜

PCB布线和灌铜

PCB布线和灌铜 综述&#xff1a;本文主要讲述AD软件中PCB布线的步骤和灌铜的操作。 一、PCB布线 1. 连接信号线 点击“N”→“隐藏连接”→“网络”&#xff0c;连接信号线&#xff0c;尽量走线短且尽量少打孔。单击界面下放的“top”和“bottom”可以实现不同层的绘制线路…
阅读更多...
51单片机学习笔记——LED闪烁和流水灯

51单片机学习笔记——LED闪烁和流水灯

任务分析 首先要知道LED闪烁主要是怎么工作的&#xff0c;闪烁亮灭自然是一下为高一下为低&#xff0c;亮灭的频率则需要延时来进行控制。 上节已经知道了如何点亮那延时如何做呢首先先编写主框架 这样是否可以通过循环将LED灯一直循环闪烁。 以为while一直在循环所以其实是可…
阅读更多...
PCB中常用电子器件封装学习——【一网打尽】

PCB中常用电子器件封装学习——【一网打尽】

‘ 上图是这个世界上大概所有的封装种类&#xff0c;当然我们日常硬件电路设计肯定用不到这么多&#xff0c;接下来我将介绍几种工程上常用的封装&#xff0c;配以图片方便大家理解学习。在电子器件选型的时候&#xff0c;避免选择到一些非常难以焊接的封装电子器件。
阅读更多...
权限提升-Windows权限提升篇数据库篇MYSQLMSSQLORACLE自动化项目

权限提升-Windows权限提升篇数据库篇MYSQLMSSQLORACLE自动化项目

知识点 1、Web到Win-数据库提权-MSSQL 2、Web到Win-数据库提权-MYSQL 3、Web到Win-数据库提权-Oracle 章节点&#xff1a; 1、Web权限提升及转移 2、系统权限提升及转移 3、宿主权限提升及转移 4、域控权限提升及转移 基础点 0、为什么我们要学习权限提升转移技术&#xff1…
阅读更多...
STM32之HAL开发——系统定时器（SysTick）

STM32之HAL开发——系统定时器（SysTick）

系统定时器&#xff08;SysTick&#xff09;介绍 SysTick—系统定时器是属于 CM3 内核中的一个外设&#xff0c;内嵌在 NVIC 中。系统定时器是一个 24bit的向下递减的计数器&#xff0c;计数器每计数一次的时间为 1/SYSCLK&#xff0c;一般我们设置系统时钟 SYSCLK等于 72M。当…
阅读更多...
Django(一)- 环境搭建和快速入门

Django(一)- 环境搭建和快速入门

一、搭建环境 1、创建Python虚拟环境 (base) C:\Users\35351>conda create -n django_study python3.9 2、安装Django (django_study) C:\Users\35351>pip install Django >> 查看安装版本 (django_study) C:\Users\35351>python -m django --version 3、安…
阅读更多...
使用倒模耳机壳UV树脂胶液制作舞台监听耳返入耳式耳机壳有哪些缺点？

使用倒模耳机壳UV树脂胶液制作舞台监听耳返入耳式耳机壳有哪些缺点？

使用倒模耳机壳UV树脂胶液制作舞台监听耳返入耳式耳机壳也存在一些缺点&#xff0c;具体如下&#xff1a; 成本较高&#xff1a;相对于传统的塑料或金属材料&#xff0c;UV树脂胶液的成本较高&#xff0c;需要更多的材料和工艺成本。制作难度较大&#xff1a;由于UV树脂的特殊…
阅读更多...
基于大数据的空气质量预测和可视化分析

基于大数据的空气质量预测和可视化分析

城市空气质量数据采集系统设计与实现 &#x1f3d9;️ 研究背景 &#x1f32c;️ 城市化与环境挑战&#xff1a;随着城市化进程的加快&#xff0c;环境污染问题&#xff0c;尤其是空气质量问题&#xff0c;已成为公众关注的焦点。数据监测的重要性&#xff1a;城市空气质量数…
阅读更多...
海尔洗空气型号KFR-72LW/09HAA81U1技术分析

海尔洗空气型号KFR-72LW/09HAA81U1技术分析

海尔洗空气型号为:KFR-72LW/09HAA81U1 室外机包含阀门地脚的安装尺寸是960宽703高400深mm 室外机铭牌参数: 制冷运行时 制冷量&#xff1a;7200W&#xff08;1100-9150&#xff09; 最大输入功率&#xff1a;3550W 最大电流&#xff1a;16.2A 制热运行时 制热量&#xff1a;980…
阅读更多...
Spark Streaming DStream

Spark Streaming DStream

Spark Streaming DStream DStream 即Discretized Stream&#xff0c;中文叫做离散流&#xff0c;Spark Streaming提供的一种高级抽象&#xff0c;代表了一个持续不断的数据流。 DStream可以通过输入数据源来创建&#xff0c;比如Kafka、Flume&#xff0c;也可以通过对其他DS…
阅读更多...
Arduino智能家居

Arduino智能家居

文章目录 一、接线框图1、下载fritzing 二、Arduino IDE 下载三、实现代码 一、接线框图 1、下载fritzing https://github.com/fritzing/fritzing-app/releases打开的软件界面如下&#xff1a; 二、Arduino IDE 下载 官网地址 P.S. 如果upload代码过程中出现cant open de…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023