函数依赖
如果给定一个X,能唯一确定一个Y,就称X确定Y,或者说Y依赖于X,例如Y = X*X函数。
X -> Y(X确定Y,Y依赖于X)
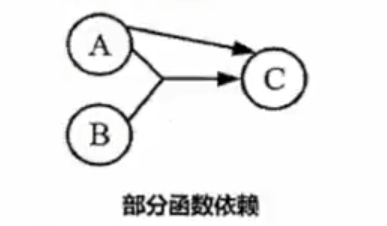
部分函数依赖
A可确定C,(A,B)也可确定C,(A,B)中的一部分(即A)可以确定C,称为部分函数依赖
A -> C
AB -> C
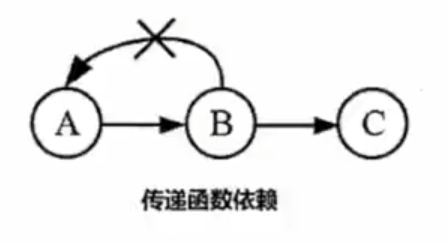
传递函数依赖
当A和B不等价时,A可确定B,B可确定C,则A可确定C,是传递函数依赖;若A和B等价则不存在传递,直接就可确定C。
A -> B
B -> C
=> A -> C
- 候选键:唯一标识表的属性或者属性组合。(候选键可以有多个)
- 学生(学号,姓名,年龄,身份证号) 学号和身份证号都可以唯一标识,所以有两个候选键,一个是学号,一个是身份证号。
- 主键:任选一个候选键,即可作为主键。
- 既可以选择学号为主键或者可以选择身份证号为主键。
- 外键:其他表中的主键。
- 主属性:候选键内的属性为主属性,其他属性为非主属性。
公理系统
设关系模式R<U,F>,U是关系模式R的属性全集,F是关系模式R的一个函数依赖集。对于R<U,F>来说有以下的:
- 自反律:若Y⊆X⊆U,则X->Y为F所逻辑蕴含
- 增广律:若X->Y为F所逻辑蕴含,且Z⊆U,则XZ -> YZ为F所逻辑蕴含
- 传递律:若X -> Y和Y -> Z为F所逻辑蕴含,则X -> Z为F所逻辑蕴含
- 合并规则:若X -> Y,X -> Z,则X -> YZ为F所蕴含
- 伪传递率:若X -> Y,WY -> Z,则XW -> Z为F所蕴含
- 分解规则:若X -> Y,Z⊆Y,则 X -> Z为F所蕴含
范式
第一范式
第一范式1NF:关系中的每一个分量必须是一个不可分的数据项。
举例:一张学生表(基本关系)如下:
| 学号 | 学生姓名 | 所在系 | 系主任名称 | 课程号 | 成绩 |
|---|---|---|---|---|---|
| 201102 | 张明 | 计算机系 | 张三 | 04 | 70 |
| 201103 | 王红 | 计算机系 | 张三 | 05 | 60 |
| 201103 | 王红 | 计算机系 | 张三 | 04 | 80 |
| 201103 | 王红 | 计算机系 | 张三 | 06 | 87 |
| 201104 | 李青 | 机械系 | 王五 | 09 | 79 |
学生表中的属性(字段),都是一个不可分的数据项,所以上述学生表是第一范式。
第一范式存在很多问题,比如大量的冗余,关系不明确等,所以需要改造到第二范式
第二范式
第二范式2NF:如果关系R属于1NF,且每一个非主属性完全函数依赖于任何一个候选码,则R属于2NF。通俗的说,2NF就是在1NF的基础上,表中的每一个非主属性不会依赖复合主键中的某一个列。
第二范式的本质是消除了部分函数依赖。
- 候选键:主属性
- 非候选键:非主属性
分析依赖关系:
- 学号 -> 学生姓名
- 学号 -> 系名
- 系名 -> 系主任名称
- (学号,课程号)-> 成绩
候选键:学号+课程号(联合候选键,本质是一个候选键,不是多个候选键)
函数依赖:候选键的一部分可以决定非主属性,称为函数依赖。
从上述依赖关系和函数依赖的定义可以推出表中的函数依赖为:
- 学号 -> 学生姓名
- 学号 -> 系名
总结:如果候选键为单属性,那么必然不存在部分函数依赖。
通过拆表,消除部分函数依赖,以满足2NF,可以将学生表拆为以下两张表:
- 学生表(学号,学生姓名,系名,系主任)
- 2NF
- 学号 -> 学生姓名
- 学号 -> 系名 -> 系主任
- 选课表(学号,课程号,成绩)
- 2NF
- 学号 + 课程号 -> 成绩
学生表
| 学号 | 学生姓名 | 系名 | 系主任 |
|---|---|---|---|
| 201102 | 张明 | 计算机系 | 张三 |
| 201103 | 王红 | 计算机系 | 张三 |
| 201104 | 李青 | 机械系 | 王五 |
选课表
| 学号 | 课程号 | 成绩 |
|---|---|---|
| 201102 | 04 | 70 |
| 201103 | 05 | 60 |
| 201103 | 04 | 80 |
| 201103 | 06 | 87 |
| 201104 | 09 | 79 |
经过拆表,学生表从1NF拆分为两个满足2NF的表。
第三范式
第三范式3NF:在满足2NF的基础上,表中不存在非主属性对候选键的传递依赖。
第二范式的本质是消除了传递函数依赖。
- 学生表(学号,学生姓名,系名,系主任)
- 2NF
- 学号 -> 学生姓名
- 学号 -> 系名 -> 系主任(传递函数依赖,不满足3NF)
- 选课表(学号,课程号,成绩)
- 2NF
- 学号 + 课程号 -> 成绩
继续拆表,消除传递函数依赖,以满足3NF:
- 学生表(学号,学生姓名,系名,系主任)
- 3NF
- 学号 -> 学生姓名
- 学号 -> 系名
- 系表
- 3NF
- 系名 -> 系主任
- 选课表(学号,课程号,成绩)
- 3NF
- 学号 + 课程号 -> 成绩
学生表
| 学号 | 学生姓名 | 系名 |
|---|---|---|
| 201102 | 张明 | 计算机系 |
| 201103 | 王红 | 计算机系 |
| 201104 | 李青 | 机械系 |
系表
| 系名 | 系主任 |
|---|---|
| 计算机系 | 张三 |
| 机械系 | 王五 |
选课表
| 学号 | 课程号 | 成绩 |
|---|---|---|
| 201102 | 04 | 70 |
| 201103 | 05 | 60 |
| 201103 | 04 | 80 |
| 201103 | 06 | 87 |
| 201104 | 09 | 79 |
优化
名称字段不适合作为主键,系表可以通过设计系编号来解决。
学生表
| 学号 | 学生姓名 | 系编号 |
|---|---|---|
| 201102 | 张明 | computer |
| 201103 | 王红 | machine |
| 201104 | 李青 | machine |
PK:学号
FK:系编号
系表
| 系编号 | 系名 | 系主任 |
|---|---|---|
| computer | 计算机系 | 张三 |
| machine | 机械系 | 王五 |
PK:系编号
选课表
| 学号 | 课程号 | 成绩 |
|---|---|---|
| 201102 | 04 | 70 |
| 201103 | 05 | 60 |
| 201103 | 04 | 80 |
| 201103 | 06 | 87 |
| 201104 | 09 | 79 |
PK:学号+课程号
经过以上拆分设计,所有的表都满足3NF,且没有冗余属性。