数据结构初阶之堆(C语言实现)
- 🌏 堆的概念
- 🌏 堆的模拟实现
- 🐓 堆的结构和方法接口
- 🐓 堆的方法的模拟实现
- 🙊 堆的初始化
- 🙊 堆的构建
- 🙊 堆的插入
- 🙊 向上调整
- 🙊 堆的删除
- 🙊 向下调整
- 🙊 堆的数据的个数
- 🙊 堆的判空
- 🙊 堆顶元素
- 🙊 堆的销毁
- 🙊 堆排序
- 🌺 版本1 创建堆,通过push、pop进行操作 (异地操作)
- 🌺 版本2 向上调整建堆(原地操作)
- 🌺 版本3----向下调整建堆(原地操作)
- 🍀 向下调整建堆的时间复杂度分析
- 🙊 topK问题
- 🌺 topK问题的分析
- 🌺 topK问题的代码实现
- 🌺 top问题的时间复杂度和空间复杂度分析
- 🌏 测试程序
- 🐓 打印堆
- 🐓 验证是否是一个堆
- 🐓 测试程序
前言:在二叉树基础篇我们提到了二叉树的顺序实现,今天让我们来学习一下特殊的二叉树———堆的相关知识。

📃博客主页: 小镇敲码人
💞热门专栏:数据结构与算法
🚀 欢迎关注:👍点赞 👂🏽留言 😍收藏
🌏 任尔江湖满血骨,我自踏雪寻梅香。 万千浮云遮碧月,独傲天下百坚强。 男儿应有龙腾志,盖世一意转洪荒。 莫使此生无痕度,终归人间一捧黄。🍎🍎🍎
❤️ 什么?你问我答案,少年你看,下一个十年又来了 💞 💞 💞
🌏 堆的概念
堆是一种完全二叉树,但是其节点值满足一些特定的规则,又分为小堆和大堆,小堆是任意根节点的值都小于等于它子树的节点值,大堆是任意根节点的值都大于等于它子树的值。
小堆:
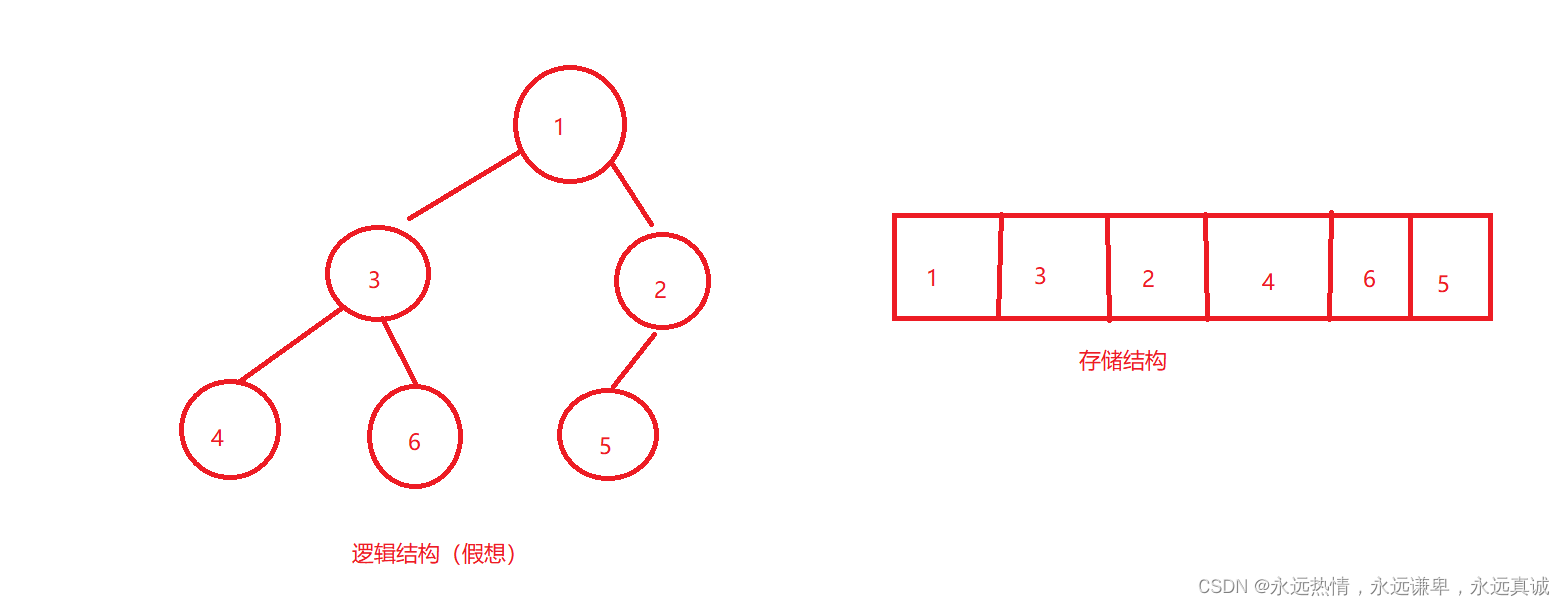
大堆:
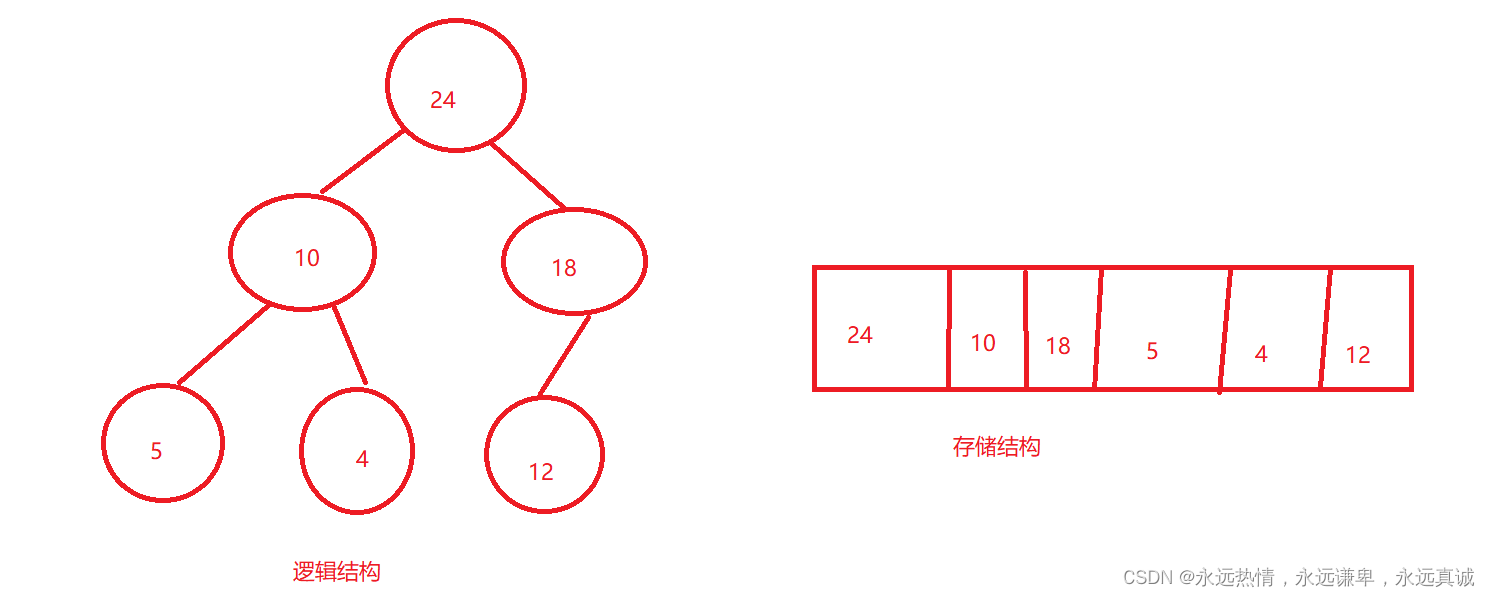
注意:不管是大堆还是小堆,其同一层的节点大小可任意。
🌏 堆的模拟实现
🐓 堆的结构和方法接口
在二叉树部分我们曾经提到,堆是一种完全二叉树,所以其使用顺序存储是不会浪费空间的,而顺序存储就是我们常说的动态顺序表。
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdbool.h>
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<string.h>
typedef int HPDataType;
typedef struct Heap
{
HPDataType* _a;
int _size;
int _capacity;
}Heap;
//堆的初始化
void HeapInit(Heap* hp);
// 堆的构建(直接给一个数组)
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
//HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
//向上调整建堆
void AdjustUp(HPDataType* a, int child);
//向下调整
void AdjustDown(HPDataType* a, int parent, int n);
//两数交换
void Swap(HPDataType* hp1, HPDataType* hp2);
//打印堆
void HeapPrint(Heap* hp);
//堆排序
void Heapsort(HPDataType* a, int n);
🐓 堆的方法的模拟实现
下面我们的方法我们都默认建一个小堆。
🙊 堆的初始化
堆的初始化很简单,我们将其对应的指针置空,元素个数和空间大小置0即可。
//堆的初始化
void HeapInit(Heap* hp)
{
assert(hp);//hp不为空
hp->_a = NULL;//指针置为空
hp->_capacity = hp->_size = 0;//元素和空间大小置为0
}
🙊 堆的构建
给你一个数组,你应该如何建一个小堆呢?我们来画图分析:
// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n)
{
assert(hp);//断言,防止hp为空
hp->_a = (HPDataType*)malloc(sizeof(HPDataType) * n);//为存节点的数组申请空间
hp->_size = hp->_capacity = n;//更新空间大小和元素大小
memcpy(hp->_a, a, sizeof(HPDataType) * n);//将数组里的值copy到我们的数据域里面
//向上调整建一个小堆
for (int i = 1; i < n; i++)
{
AdjustUp(hp->_a,i);
}
}
图解代码:
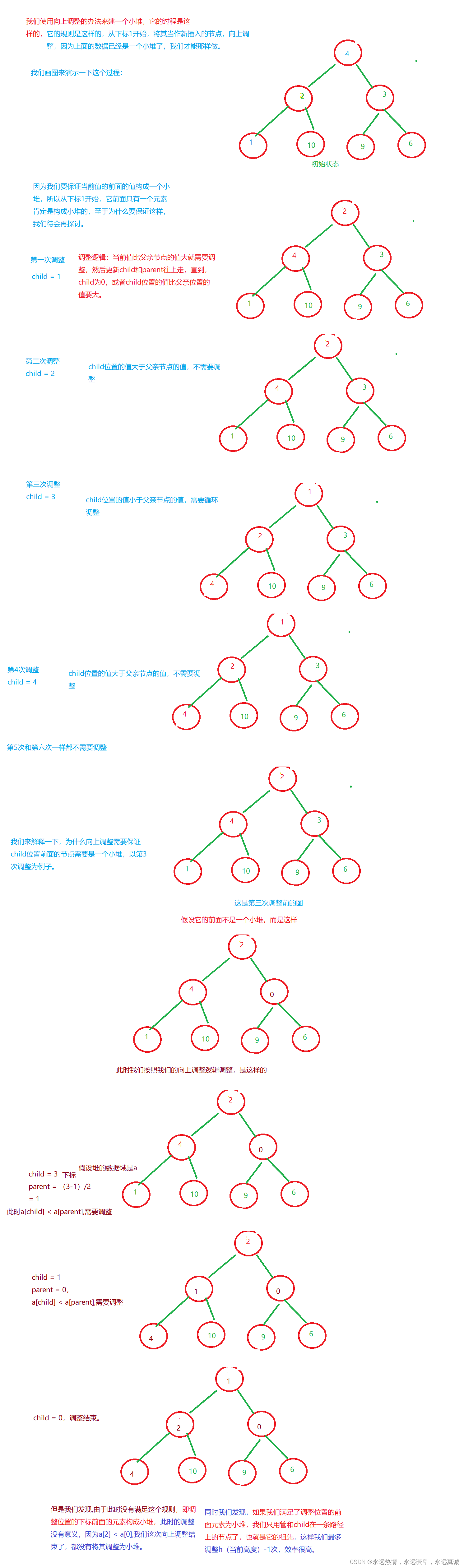
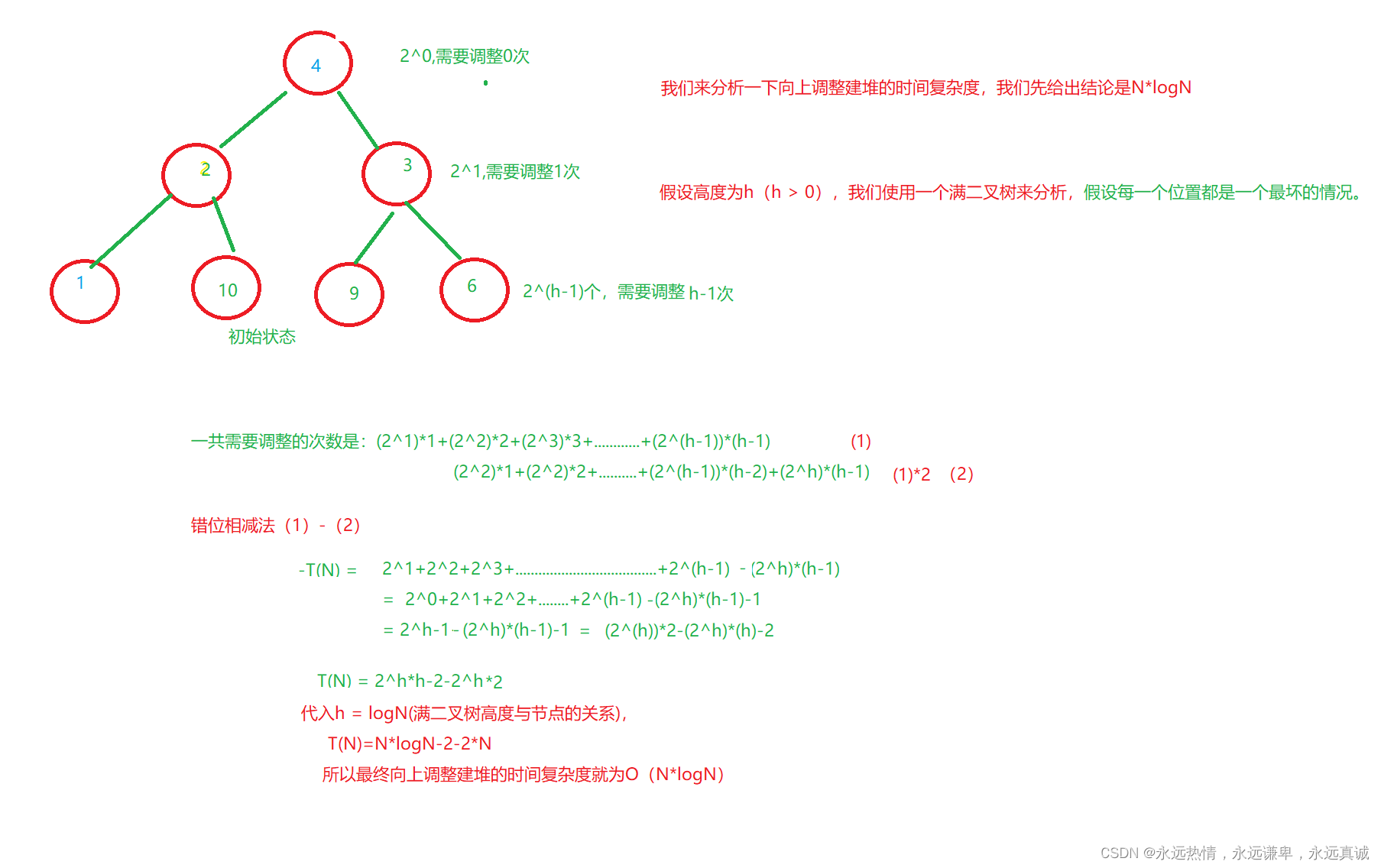
向下调整建堆的时间复杂度分析:
🙊 堆的插入
堆的插入应该如何实现呢?我们直接插入到线性表尾部就行,由于插入前是堆,所以我们走一个向上调整就可以将其调整为堆。
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{
assert(hp);//断言,防止hp为空
if (hp->_size == hp->_capacity)//扩容
{
hp->_capacity = hp->_capacity == 0 ? 4 : hp->_capacity * 2;
HPDataType* tmp = (HPDataType*)realloc(hp->_a,sizeof(HPDataType) * hp->_capacity);
if (tmp == NULL)
{
perror("realloc failed\n");
exit(-1);
}
hp->_a = tmp;
}
hp->_a[hp->_size] = x;//插入
hp->_size++;
//向上调整
AdjustUp(hp->_a,hp->_size - 1);//在插入位置走一个向上调整
}
🙊 向上调整
上面已经分析过了。
//向上调整建小堆
void AdjustUp(HPDataType* a, int child)
{
assert(a);//a不为空
int parent = (child - 1) / 2;//找到child的父亲节点,和其比较看是否需要调整
while (child > 0)
{
if (a[child] < a[parent])//建一个小堆,如果孩子节点比父亲节点的值小,需要调整
{
Swap(&a[child], &a[parent]);//交换
child = parent;//将父亲节点的值给孩子,继续在这条路径上调整
parent = (parent - 1) / 2;//更新父亲节点的下标
}
else
{
break;//孩子节点的值已经大于等于父亲节点的值了,不需要再继续调整
}
}
}
🙊 堆的删除
堆的删除我们是删除堆顶的数据,因为这个数据最值得去删,什么意思呢?举个例子1.因为删除最后一个节点不会改变堆的结构没什么意义,2.堆顶数据要么是最大值,要么是最小值,很特殊。
那我们应该如何实现堆的删除呢?我们还是画图来分析:
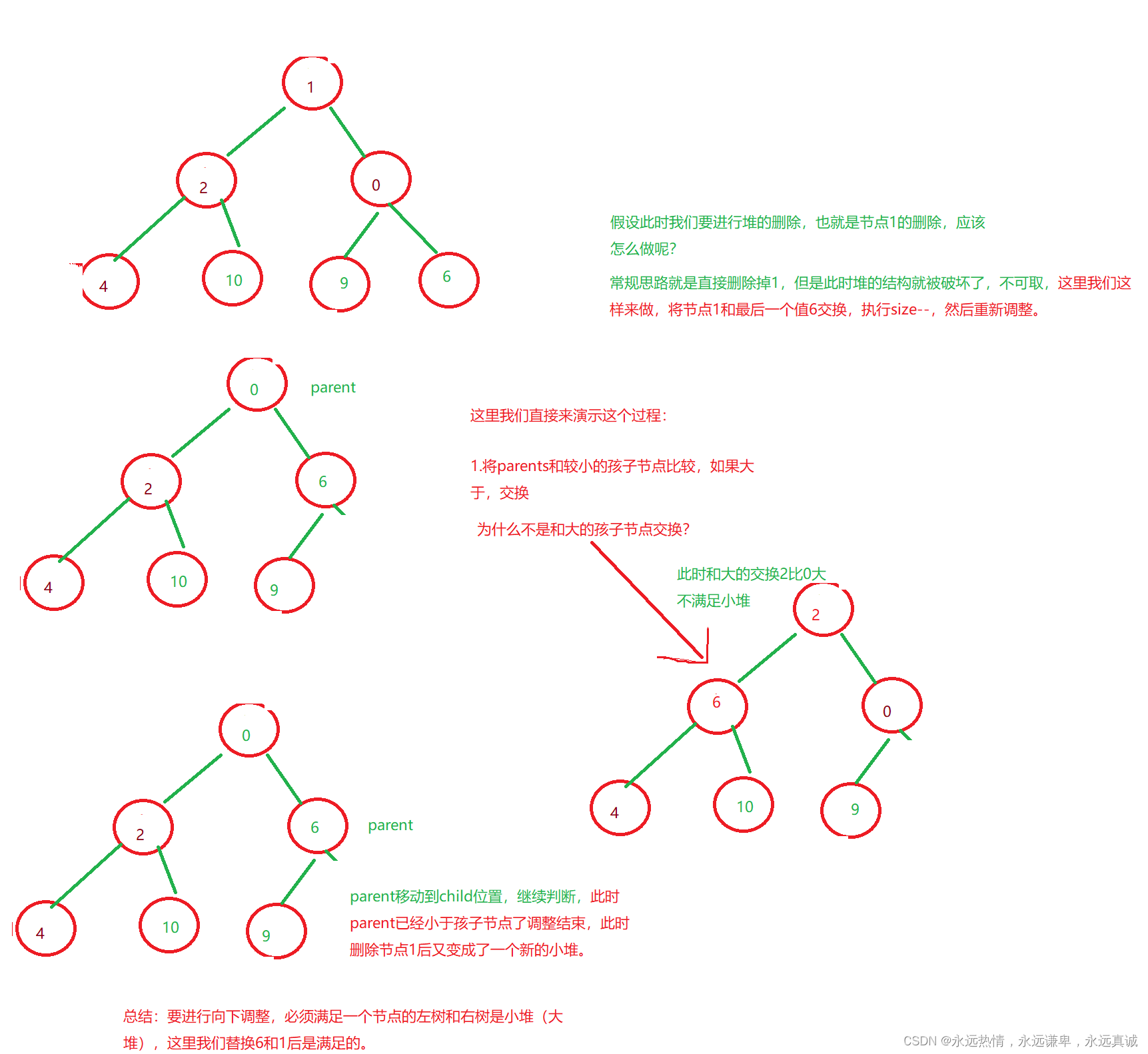
代码实现:
// 堆的删除
void HeapPop(Heap* hp)
{
assert(hp);//hp不为空
assert(hp->_size > 0);//堆的元素个数要大于0
Swap(&hp->_a[0], &hp->_a[hp->_size - 1]);//交换堆顶元素和最后一个元素的值
hp->_size--;//_size--
//向下调整
AdjustDown(hp->_a, 0, hp->_size);//根节点左树和右树为小堆,可以向下调整
}
🙊 向下调整
这个我们上面也已经分析了,直接给代码:
//向下调整(小堆)
void AdjustDown(HPDataType* a, int parent, int n)
{
assert(a);//a不为空
int child = parent * 2 + 1;//先假设最小的孩子是左孩子
while (child < n)
{
//找出最小的孩子
if (child+1 < n && a[child] > a[child + 1])//如果右孩子存在且右孩子的值比左孩子更小
{
child = child + 1;
}
if (a[child] < a[parent])//最小的孩子比parent的值小,就交换
{
Swap(&a[child], &a[parent]);
parent = child;//更新parent
child = parent * 2 + 1;//更新child,也假设最小的孩子是左孩子
}
else//最小的孩子比父亲节点的值大,已经不需要调整,是小堆了。
{
break;
}
}
}
🙊 堆的数据的个数
直接返回_size的值。
// 堆的数据个数
int HeapSize(Heap* hp)
{
assert(hp);//hp不为空
return hp->_size;
}
🙊 堆的判空
如果_size不为0,堆就不为空。
// 堆的判空
int HeapEmpty(Heap* hp)
{
assert(hp);
if (hp->_size == 0)//为空返回1
return 1;
else//不为空返回0
return 0;
}
🙊 堆顶元素
堆顶元素在下标为0的位置。
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{
assert(hp);
assert(hp->_size > 0);
return hp->_a[0];
}
🙊 堆的销毁
堆的销毁实际上主要要做的就是回收在堆上开的空间,将相应的指针置为空,空间和元素大小置为0。
// 堆的销毁
void HeapDestory(Heap* hp)
{
assert(hp);//hp不为空
assert(hp->_size > 0);//元素个数要大于0
free(hp->_a);//释放空间
hp->_a = NULL;//将动态数组的指针置为空
hp->_capacity = hp->_size = 0;//将空间和元素大小置为0
}
🙊 堆排序
由于小堆和大堆的堆顶元素都是最小或者最大的,所以我们pop堆顶元素,然后再剩下的元素调整,就能得到一个有序的序列。
🌺 版本1 创建堆,通过push、pop进行操作 (异地操作)
那我们该如何实现这个堆排序呢?下面的代码可以吗为什么?
void Heapsort(HPDataType* a, int n)
{
Heap hp1;//假设我们建一个小堆
HeapInit(&hp1);
for (int i = 0; i < n; ++i)
{
HeapPush(&hp1, a[i]);//插入对应元素
}
for (int i = 0; i < n; ++i)
{
a[i] = HeapTop(&hp1);//将最小的元素依次给数组
HeapPop(&hp1);//pop堆顶元素
}
}
效果演示:
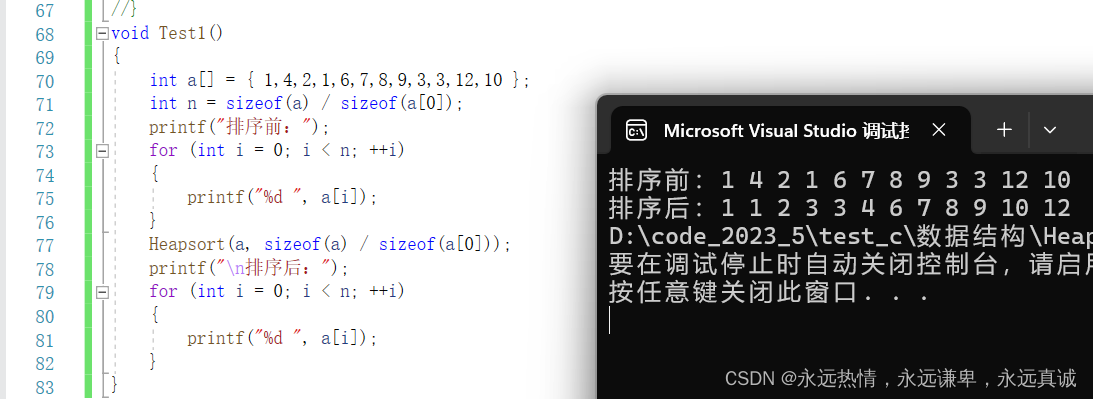
这种方法是不太好的,因为先暂且不谈时间复杂度的问题,我们为了去给数组排一个序,而建了一个堆,这个空间开销是没必要的,其实我们可以对数组原地建堆。
🌺 版本2 向上调整建堆(原地操作)
//堆排序,向上调整
void Heapsort2(HPDataType* a, int n)
{
assert(a);
for (int i = 1; i < n; i++)//我们向上调整,原地建一个小堆
{
AdjustUp(a,i);
}
for (int end = n - 1; end >= 0; --end)
{
Swap(&a[0], &a[end]);//将堆顶元素放到堆最后面去
AdjustDown(a, 0, end);//此时的end就代表我们的元素个数
}
}
原地建堆,如果你想排降序,就需要建一个小堆,因为小堆的堆顶元素是最小的,我们原地操作,就可以将最小的和最后一个元素交换,这样没有破坏原来的结构,走一个向下调整就可以恢复堆结构。
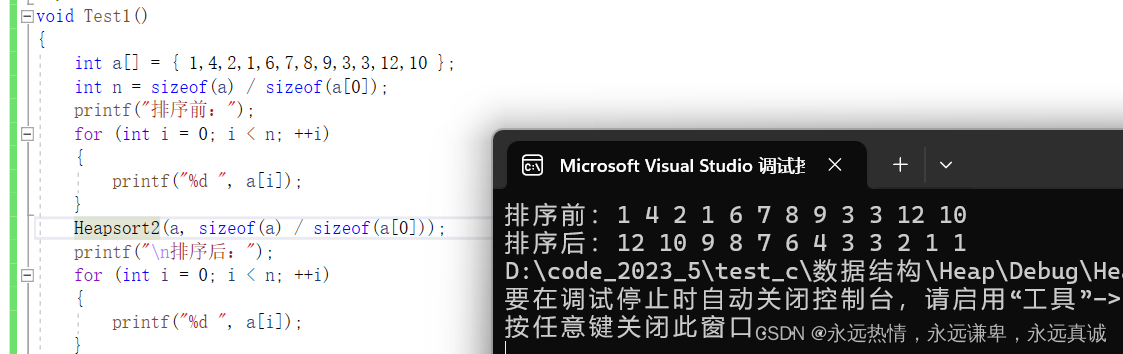
时间复杂度:NlogN,向上调整建堆:NlogN,向下调整调整一次logN(一共调整了N次),所以总体的时间复杂度也是O(N*logN)。
🌺 版本3----向下调整建堆(原地操作)
但是这样就结束了吗,我们发现如果使用上面这种方法,既要写一个向上调整,也要写一个向下调整,我只是想排个序,需要这么复杂吗,难道就不能直接向下调整建堆吗?这样我就不用写两个了呀,调整那块肯定要用向下调整的,不然就破坏堆的结构了。
下面我们来介绍向下调整建堆

代码实现:
//堆排序,向下调整
void Heapsort3(HPDataType* a, int n)
{
assert(a);
for (int i = (n-1-1)/2; i >= 0; i--)//我们向上调整,原地建一个小堆
{
AdjustDown(a,i,n);
}
for (int end = n - 1; end >= 0; --end)
{
Swap(&a[0], &a[end]);//将堆顶元素放到堆最后面去
AdjustDown(a, 0, end);//此时的end就代表我们的元素个数
}
}
运行结果:
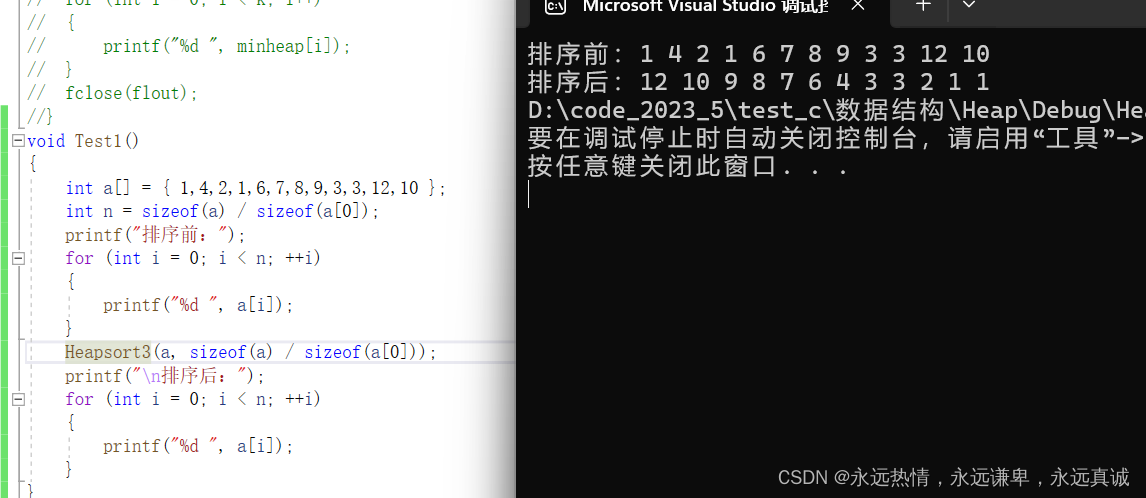
🍀 向下调整建堆的时间复杂度分析
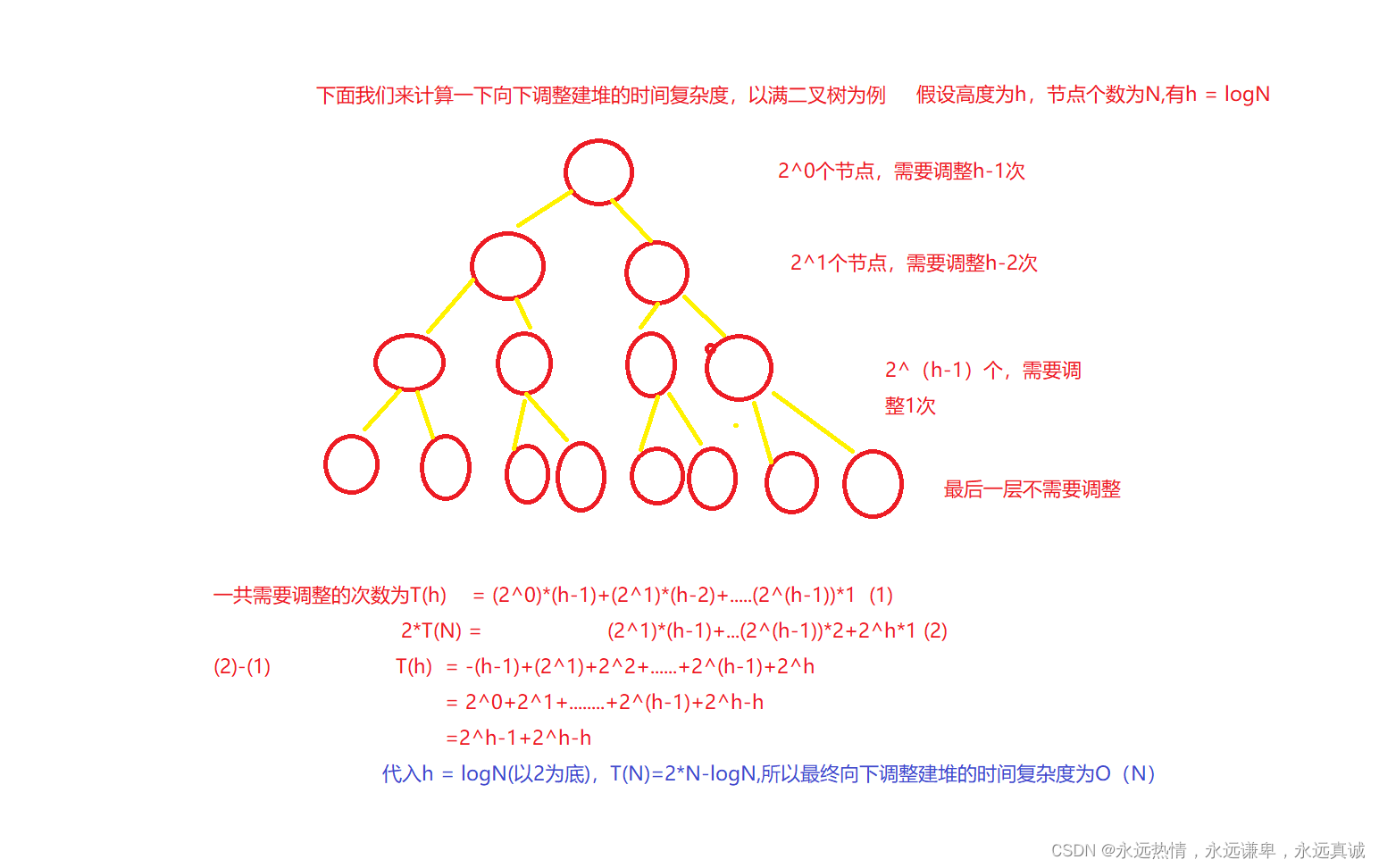
整体这种堆排序的时间复杂度也是O(N*logN),建堆的消耗是O(N),但是每一次调整的消耗还是logN,调整了次,量级还是和第二种一样,但是向下调整建堆只需要写一个向下调整,且向下调整建堆比向上调整建堆要更快。
🙊 topK问题
topK问题指的是让我们求第K大,第K小等问题,思考一下,在一个乱序的数组里面,如果我们想要这样来做,我们常规的解决办法是什么?排序!!!这样来做的时间复杂度是N*logN,我们只是求第K大或者第K小的数,有必要把这些数全部排一遍顺序吗,答案是不用,下面让我们来学习一下使用堆这种数据结构来解决经典的topK问题。
🌺 topK问题的分析
下面我们画图来分析一下topk问题具体的解决之道。
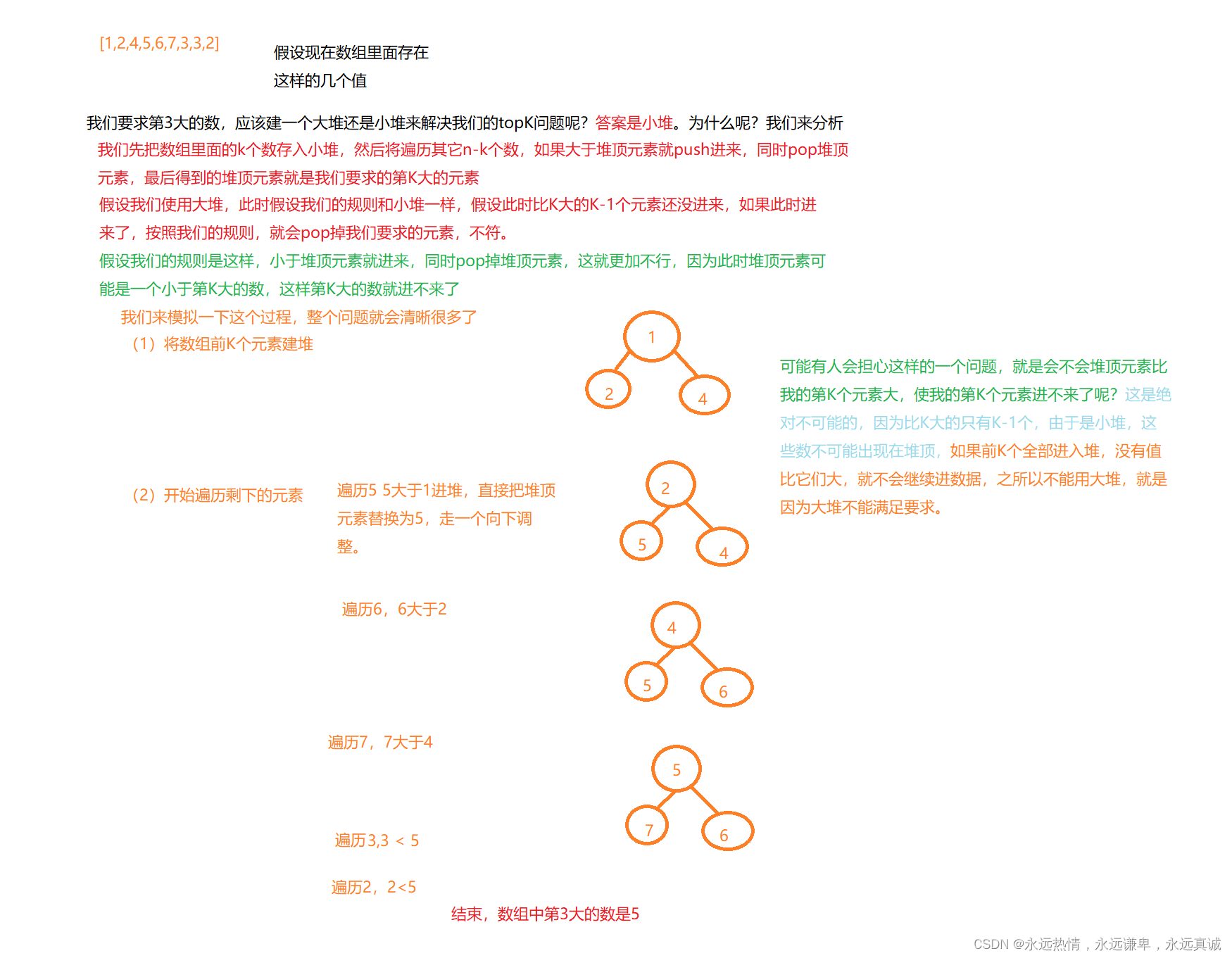
🌺 topK问题的代码实现
我们使用C语言的文件操作,造了100w个小于100w的数据(随机值),然后我们求前5个大的数,我们这样来验证,把文件里任意5个数改为大于100w的数,如果最后打印出来是我们改的5个数,证明我们的topk问题得到解决。
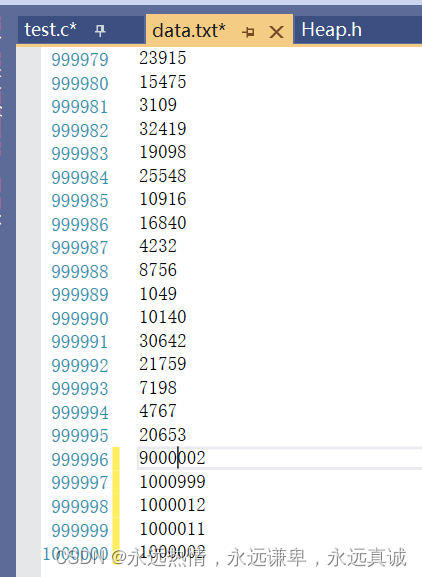
可以看到我们改了最后5个数,修改之后把创建数据的程序注释掉,防止它重新生成,我们的修改就没意义了。
代码实现:
void CreateNDate()
{
// 造数据
int n = 1000000;
srand(time(0));
const char* file = "data.txt";
FILE* fin = fopen(file, "w");
if (fin == NULL)
{
perror("fopen error");
return;
}
for (size_t i = 0; i < n; ++i)
{
int x = rand() % 1000000;//造随机数据,可以让我们的测试程序得到更好的检查
fprintf(fin, "%d\n", x);//将数据放入文件
}
fclose(fin);
}
void PrintTopK(int k)
{
const char* file = "data.txt";//定义文件
FILE* flout = fopen(file, "r");
if (flout == NULL)
{
perror("fopen failed");
exit(-1);
}
//开一个数组存放k个数据,开一个小堆
HPDataType* minheap = (HPDataType*)malloc(sizeof(HPDataType) * k);
if (minheap == NULL)
{
perror("malloc failed");
exit(-1);
}
for (int i = 0; i < k; i++)//将k个数放入数组中
{
fscanf(flout, "%d", &minheap[i]);
}
//向下调整建堆
for (int i = (k - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(minheap, i, k);
}
//遍历,如果大于小堆堆顶的数据的话,就和它换,并向下调整
int x = 0;
while (fscanf(flout, "%d", &x) != EOF)
{
if (x > minheap[0])
{
Swap(&x, &minheap[0]);
AdjustDown(minheap, 0,k);
}
}
for (int i = 0; i < k; i++)//打印前k大的数
{
printf("%d ", minheap[i]);
}
fclose(flout);//关闭文件
}
int main()
{
CreateNDate();//造10w个数据
PrintTopK(5);
return 0;
}
运行结果:
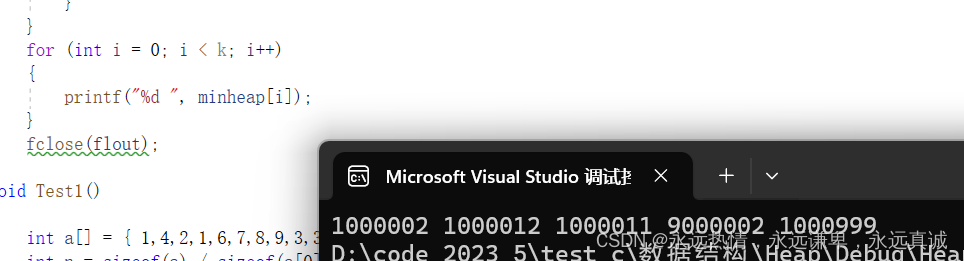
可以看到预期结果和我们修改的数是一致的,说明我们的代码应该没啥问题。
🌺 top问题的时间复杂度和空间复杂度分析

🌏 测试程序
下面我们来测试一下我们写的上述方法的正确性如何。
🐓 打印堆
我们可能需要把堆打印出来看结果。
//打印堆
void HeapPrint(Heap* hp)
{
assert(hp);
assert(hp->_size > 0);
for (int i = 0; i < hp->_size; i++)
{
printf("%d ", hp->_a[i]);
}
printf("\n");
}
🐓 验证是否是一个堆
我们应该如何验证我们的数据是否是一个小堆呢?其实很简单,数组是顺序存储的,我们的数据一定是完全二叉树,这个不用验证,关键是验证我们的数据是否都满足小堆的定义,即所有的根节点的值都比它的左子树的和右子树的根节点的值要小,我们可以走一个前序遍历来验证。
//验证是否是一个小堆
int is_Heap(HPDataType* a, int n,int root)
{
if (root >= n)
return 1;
int leftchild = root * 2 + 1;//左孩子的下标
int rightchild = root * 2 + 2;//右孩子的下标
if (leftchild < n && a[root] > a[leftchild])//左孩子存在且小于根,返回0,并打印相关信息
{
printf("%d\n位置不满足小堆", root);
return 0;
}
if (rightchild < n && a[root] > a[rightchild])//右孩子存在且小于根,返回0,并打印相关信息
{
printf("%d\n位置不满足小堆", root);
return 0;
}
return is_Heap(a, n, leftchild) && is_Heap(a, n, rightchild);//左树和右树都满足小堆就返回1
}
🐓 测试程序
void Test2()
{
Heap hp1;//建堆
HeapInit(&hp1);//初始化堆
//造10w个数据进堆
int N = 100000;
srand(time(NULL));//通过时间来初始化随机数种子
for (int i = 0; i < N; ++i)
{
HeapPush(&hp1, rand() % (10000000));//将数据存入堆里面
}
int i = is_Heap(hp1._a,N,0);//验证是否为堆
if (i)//打印提示信息
printf("是堆\n");
else
printf("不是堆\n");
printf("堆的元素个数为%d\n", HeapSize(&hp1));//验证元素个数方法是否正确
printf("堆顶元素为:%d\n", HeapTop(&hp1));//验证堆顶元素是否正确
HeapPop(&hp1);//验证pop函数是否正确
printf("堆的元素个数为%d\n", HeapSize(&hp1));
printf("堆顶元素为:%d\n", HeapTop(&hp1));
hp1._a[3] = -1;//破坏堆的结构
i = is_Heap(hp1._a, N, 0);
if (i)
printf("是堆\n");
else
printf("不是堆\n");
HeapDestory(&hp1);
if (hp1._a == NULL)
printf("销毁成功\n");
}
运行结果:









![[ C++ ] STL---反向迭代器的模拟实现](https://img-blog.csdnimg.cn/direct/2ce5b3ead752400eb974373a9dfc1611.gif)