一.移动零(. - 力扣(LeetCode))

算法思想 :
设置两个指针left,right,将数组分为三块[0,left]为不为0的元素,[left+1,right-1]为0元素,[right,num.size()-1]为未扫描的区域,判断right位置,不为0元素则与left+1位置元素交换,left++和right++;为0则只有right++,这样right扫描到最右侧时保证右侧全是0。


class Solution {
public:
void moveZeroes(vector<int>& nums){
int cur=0,dest=-1;
while(cur<nums.size())
{
if(nums[cur])
{
swap(nums[cur],nums[++dest]);
}
cur++;
}
}
};ps:数组分块扫描划分是快排的核心思想
二.排序数组
算法思想:
与移动0相似,不过这里移动指针时将数组分为四块,l,r是当前(子)数组的最左侧与右侧,用i,left,right三个指针,[l,left]为小于随机基准元素key的区域,[left+1,i-1]是key区域,[i,right-1]为未扫描区域,[right,r]为大于key的元素,移动时控制区间即可。

void qsort(vector<int>& nums,int l,int r)
{
if(l>=r) return;
int key=nums[rand()%(r-l+1)+l];
int i=l,left=l-1,right=r+1;
while(i<right)
{
if(nums[i]<key)
{
swap(nums[++left],nums[i]);
i++;
}
else if(nums[i]>key)
{
--right;
swap(nums[right],nums[i]);
}
else
{
i++;
}
}
qsort(nums,l,left);
qsort(nums,right,r);
}
class Solution {
public:
vector<int> sortArray(vector<int>& nums)
{
srand(time(NULL));
qsort(nums,0,nums.size()-1);
return nums;
}
};三.复写零
算法思想:
1.找到最后一个要复写的元素。

cur为扫描指针,dest为移动指针,初始cur为0,dest为-1;当dest移动到最后一个元素时,cur指向最后一个要复写的元素。 但这里dest可能会超出(说明cur此时指向0),所以要先判断边界位置。

2.“从后往前”复写元素。
是0就将cur位置元素赋值给dest位置和dest-1位置,然后dest-=2;非0就将cur直接赋给dest位置,dest-=1;然后都有cur--。
void duplicateZeros(vector<int>& nums)
{
//先找到最后一个数
int cur=0,dest=-1;
int tmp = nums.size() - 1;
while(dest < tmp)
{
if (nums[cur] == 0)
{
dest += 2;
}
else
{
dest += 1;
}
if (dest >= tmp) break;
cur++;
}
//判断边界情况,如果超出,就事先处理
if(dest>nums.size()-1)
{
cur--;
dest-=2;
nums[nums.size()-1]=0;
}
//从后向前复写
for(;cur>=0;cur--)
{
if(nums[cur]==0)
{
nums[dest]=nums[dest-1]=0;
dest-=2;
}
else
{
nums[dest]=nums[cur];
dest--;
}
}
}四.快乐数(. - 力扣(LeetCode))
算法思想:
快慢指针的思想,因为这里数字最后都会循环,只要看快指针最后在环里与满指针相遇时所在的元素是否为一即可。
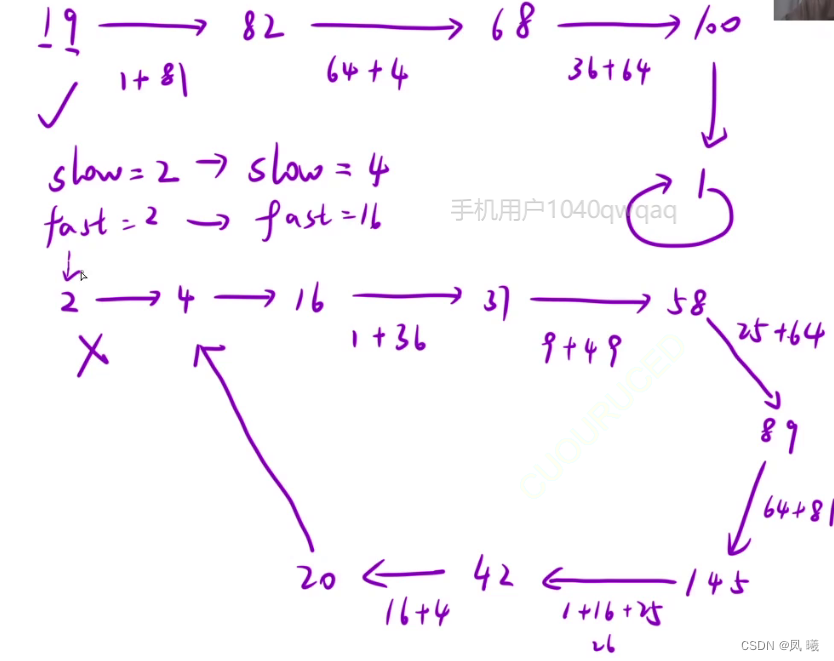
int fx(int x)
{
int sum=0;
while(x)
{
sum+=(x%10)*(x%10);
x/=10;
}
return sum;
}
class Solution {
public:
bool isHappy(int n) {
int fast=n,slow=n;
while(1)
{
slow=fx(slow);
fast=fx(fast);
fast=fx(fast);
if(fast==slow)
{
if(fast==1)
return true;
else
return false;
}
}
}
};五.盛最多水的容器(. - 力扣(LeetCode))

算法思想:
对撞指针,设置left,right指针分别向左右侧,记录盛水量,去除左/右移较小元素的位置(因为移动更大一侧不会改变最大值),记录最大值即可。
class Solution {
public:
int maxArea(vector<int>& height) {
if(height.size() <= 1) return 0;
int res = 0;//保存答案
int l = 0, r = height.size() - 1;//开始时,l指向最左边的挡板,r指向最右边的挡板
while(l < r)//如果l,r之间还有挡板
{
res = max(min(height[l], height[r]) * (r - l), res);//计算盛水值
if(height[l] <= height [r])//谁小谁以后就不用再考虑
l++;
else
r--;
}
return res;
}
};六 .有效三角形的个数(. - 力扣(LeetCode))

算法思想:
先将数组排序,利用单调性使用双指针解决 。如下图a,b,c三个指针,当left,right指向判断区间左右侧,当a+b>c时,说明a右侧的全部元素都和b,c符合,所以right--来继续判断其他组合情况,当a+b<c时,说明此时abc不符合,让left++,重新判断a+b与c。直到left==right时结束这次循环,将c--(重新选择最大数)判断剩下组合。时间复杂度O(N*N);

class Solution {
public:
int triangleNumber(vector<int>& nums) {
sort(nums.begin(),nums.end());
int sum=0;
for(int i=nums.size()-1;i>1;i--)
{
int left=0,right=i-1;
while(left<right)
{
if(nums[left]+nums[right]>nums[i])
{
sum+=right-left;
right--;
}
else
{
left++;
}
}
}
return sum;
}
};七.三数之和 (. - 力扣(LeetCode))

算法思想:
先排序,利用单调性用双指针解决问题。即依旧a(left),b(right),c三个指针,c指向当次循环最大值(初始指向数组最大值),判断a+b+c与0的关系,如果a+b+c<0则a++,a+b+c>0则b--,直到找出等于0的组合并记录下来,注意要去重操作(防止相同数字组合在一起)。当次操作完成后c--即可两层循环,时间复杂度依旧是O(N*N)。
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
vector<vector<int>> ret;
sort(nums.begin(),nums.end());
for(int i=0;i<=nums.size()-3;i++)
{
int left=i+1,right=nums.size()-1;
while(left<right)
{
if(nums[i]+nums[left]+nums[right]<0)
{
left++;
}
else if(nums[i]+nums[left]+nums[right]>0)
{
right--;
}
else
{
//记录
ret.push_back({nums[i],nums[left],nums[right]});
//去重
left++,right--;
while(left<right&&nums[left]==nums[left-1]) left++;
while(left<right&&nums[right]==nums[right+1]) right--;
}
}
while(i<=nums.size()-4&&nums[i]==nums[i+1]) i++;
}
return ret;
}
};八.长度最小的子数组(. - 力扣(LeetCode))
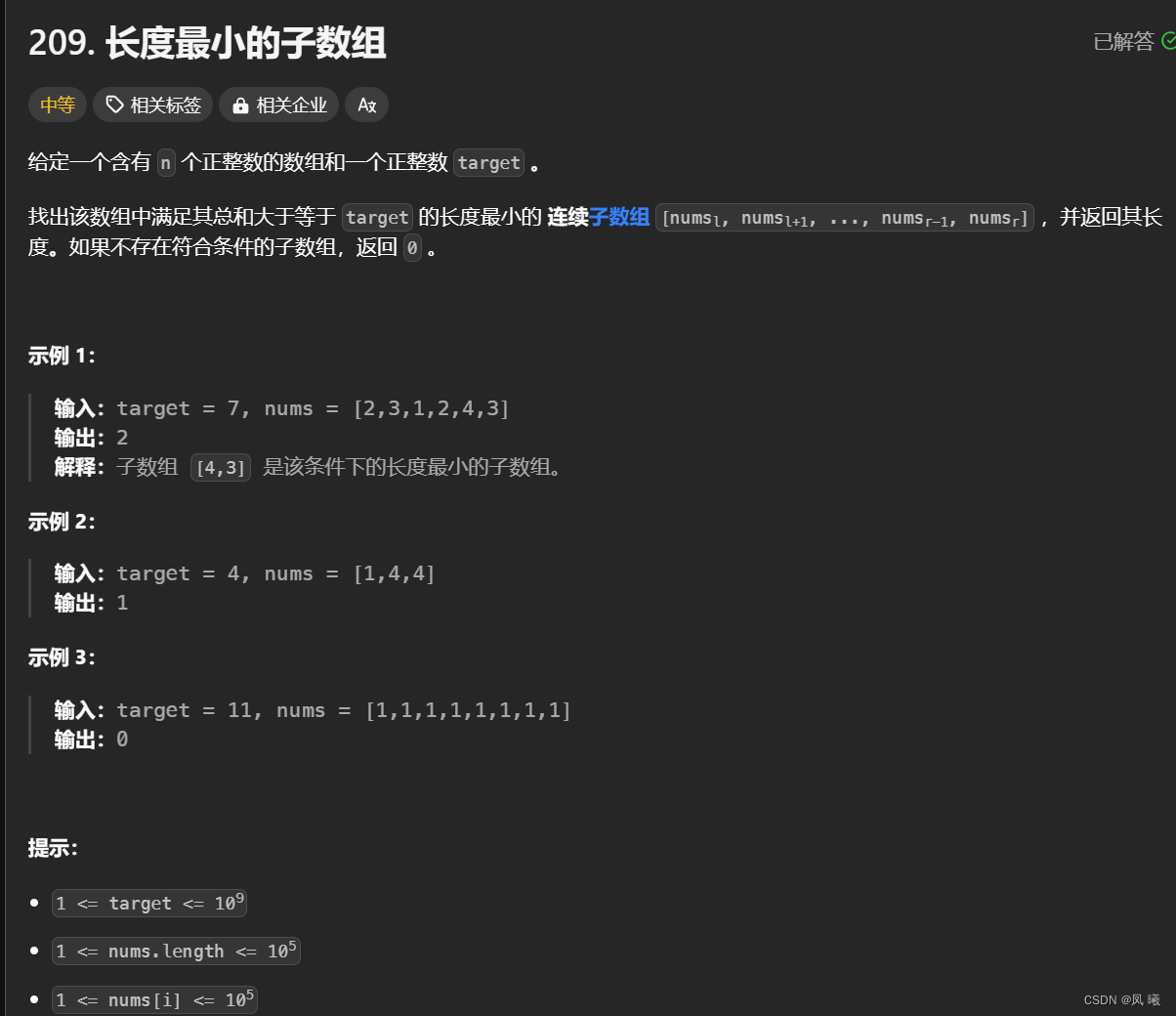
算法解析:
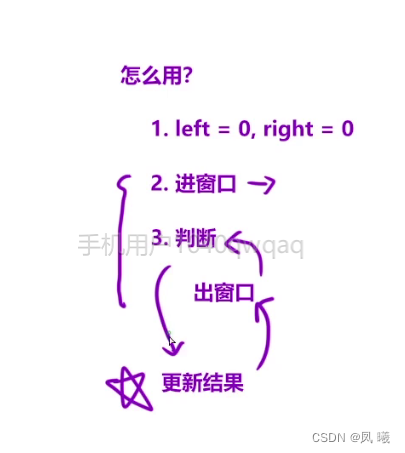
2个指针,扫描(前窗口)指针,尾指针。滑动窗口的步骤:1.扫描元素入窗口。2.判断是否需要出窗口。3.窗口向前滑动。 //记录结果这一步可以根据情况来调整位置。
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums)
{
int left=0,right=0,n=nums.size();
int sum=0,len=INT_MAX;
while(right<n)
{
//入窗口
sum+=nums[right];
//判断
while(sum>=target)
{
//更新结果
len=min(len,right-left+1);
//出窗口
sum-=nums[left++];
}
right++;
}
return len==INT_MAX?0:len;
}
};





![[MAUI]集成高德地图组件至.NET MAUI Blazor项目](https://img-blog.csdnimg.cn/direct/7057550c4f7049ee8cdc1a2f78ed55c2.gif)