算法体系-12 第十二二叉树的基本算法下

一实现二叉树的按层遍历

1.1 描述

1）其实就是宽度优先遍历，用队列

2）可以通过设置flag变量的方式，来发现某一层的结束（看题目）看下边的第四题解答

1.2 代码

public class Code01_LevelTraversalBT {

    public static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int v) {
            value = v;
        }
    }

    public static void level(Node head) {
        if (head == null) {
            return;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.add(head);
        while (!queue.isEmpty()) {
            Node cur = queue.poll();
            System.out.println(cur.value);
            if (cur.left != null) {
                queue.add(cur.left);
            }
            if (cur.right != null) {
                queue.add(cur.right);
            }
        }
    }

二实现二叉树的序列化和反序列化

2.1描述

1）先序方式序列化和反序列化

2）按层方式序列化和反序列化

将二叉树序力化为唯一的字符串叫序力化，字符串也能转出唯一的数二叉树叫反序力化

2.2 分析

2.3 前序列化代码

public static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int data) {
            this.value = data;
        }
    }

    public static Queue<String> preSerial(Node head) {
        Queue<String> ans = new LinkedList<>();
        pres(head, ans);
        return ans;
    }

    public static void pres(Node head, Queue<String> ans) {
        if (head == null) {
            ans.add(null);
        } else {
            ans.add(String.valueOf(head.value));
            pres(head.left, ans);
            pres(head.right, ans);
        }
    }

2.4 前序反序列化

public static Node buildByPreQueue(Queue<String> prelist) {
        if (prelist == null || prelist.size() == 0) {
            return null;
        }
        return preb(prelist);
    }

    public static Node preb(Queue<String> prelist) {
        String value = prelist.poll();
        if (value == null) {
            return null;
        }
        Node head = new Node(Integer.valueOf(value));
        head.left = preb(prelist);
        head.right = preb(prelist);
        return head;
    }

2.5 中序列化代码

由上图可以知道，中序序例化是有歧义的，所以不存在中序的序列化

public static Queue<String> inSerial(Node head) {
        Queue<String> ans = new LinkedList<>();
        ins(head, ans);
        return ans;
    }

    public static void ins(Node head, Queue<String> ans) {
        if (head == null) {
            ans.add(null);
        } else {
            ins(head.left, ans);
            ans.add(String.valueOf(head.value));
            ins(head.right, ans);
        }
    }

2.7 中序反列化

2.8 后序列化代码

public static Queue<String> posSerial(Node head) {
        Queue<String> ans = new LinkedList<>();
        poss(head, ans);
        return ans;
    }

    public static void poss(Node head, Queue<String> ans) {
        if (head == null) {
            ans.add(null);
        } else {
            poss(head.left, ans);
            poss(head.right, ans);
            ans.add(String.valueOf(head.value));
        }
    }

2.9后序反列化代码

public static Node buildByPosQueue(Queue<String> poslist) {
        if (poslist == null || poslist.size() == 0) {
            return null;
        }
        // 左右中  ->  stack(中右左) 默认是左右中，这种情况没法首先没法建立头节点，因此进行转化为头在前面的情况，把它放入stack(中右左)，这是头就先出来，就可以新建head
        Stack<String> stack = new Stack<>();
        while (!poslist.isEmpty()) {
            stack.push(poslist.poll());
        }
        return posb(stack);
    }

    public static Node posb(Stack<String> posstack) {
        String value = posstack.pop();
        if (value == null) {
            return null;
        }
        Node head = new Node(Integer.valueOf(value));
        head.right = posb(posstack);
        head.left = posb(posstack);
        return head;
    }

3.0 按层序列化和反序列化

3.0.1分析

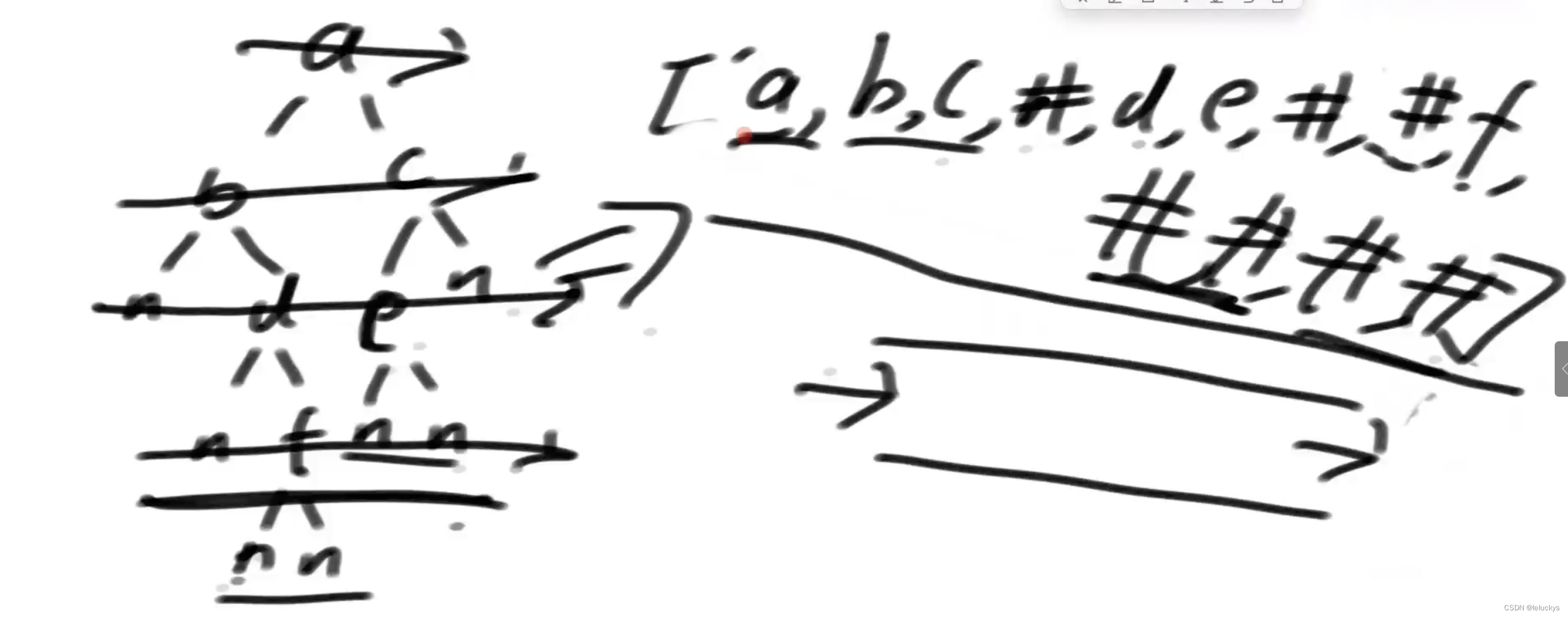3.0.2 按层序列化代码

public static Queue<String> levelSerial(Node head) {
        Queue<String> ans = new LinkedList<>();
        if (head == null) {
            ans.add(null);
        } else {
            ans.add(String.valueOf(head.value));
            Queue<Node> queue = new LinkedList<Node>();
            queue.add(head);
            while (!queue.isEmpty()) {
                head = queue.poll(); // head 父   子
                if (head.left != null) {
                    ans.add(String.valueOf(head.left.value));
                    queue.add(head.left);
                } else {
                    ans.add(null);
                }
                if (head.right != null) {
                    ans.add(String.valueOf(head.right.value));
                    queue.add(head.right);
                } else {
                    ans.add(null);
                }
            }
        }
        return ans;
    }

3.0.3 按层反序列化代码


    public static Node buildByLevelQueue(Queue<String> levelList) {
        if (levelList == null || levelList.size() == 0) {
            return null;
        }
        Node head = generateNode(levelList.poll());
        Queue<Node> queue = new LinkedList<Node>();
        if (head != null) {
            queue.add(head);
        }
  //因为要记录上一次的节点，这里借用队列来完成
        Node node = null;
        while (!queue.isEmpty()) {
            node = queue.poll();
            node.left = generateNode(levelList.poll());
            node.right = generateNode(levelList.poll());
            if (node.left != null) {
                queue.add(node.left);
            }
            if (node.right != null) {
                queue.add(node.right);
            }
        }
        return head;
    }

    public static Node generateNode(String val) {
        if (val == null) {
            return null;
        }
        return new Node(Integer.valueOf(val));
    }

三 Encode N-ary Tree to Binary Tree

3.1 描述

一颗多叉树，序历化为为二叉树，二叉树也能转为原来的多叉树；

3.2 分析

第一步先将多叉树的每个节点的孩子放在对应节点左树的右边界上；

左树的节点为该节点的第一个树，反回来看某个节点是否有孩子看该节点左数是否有右边孩子

结构如下

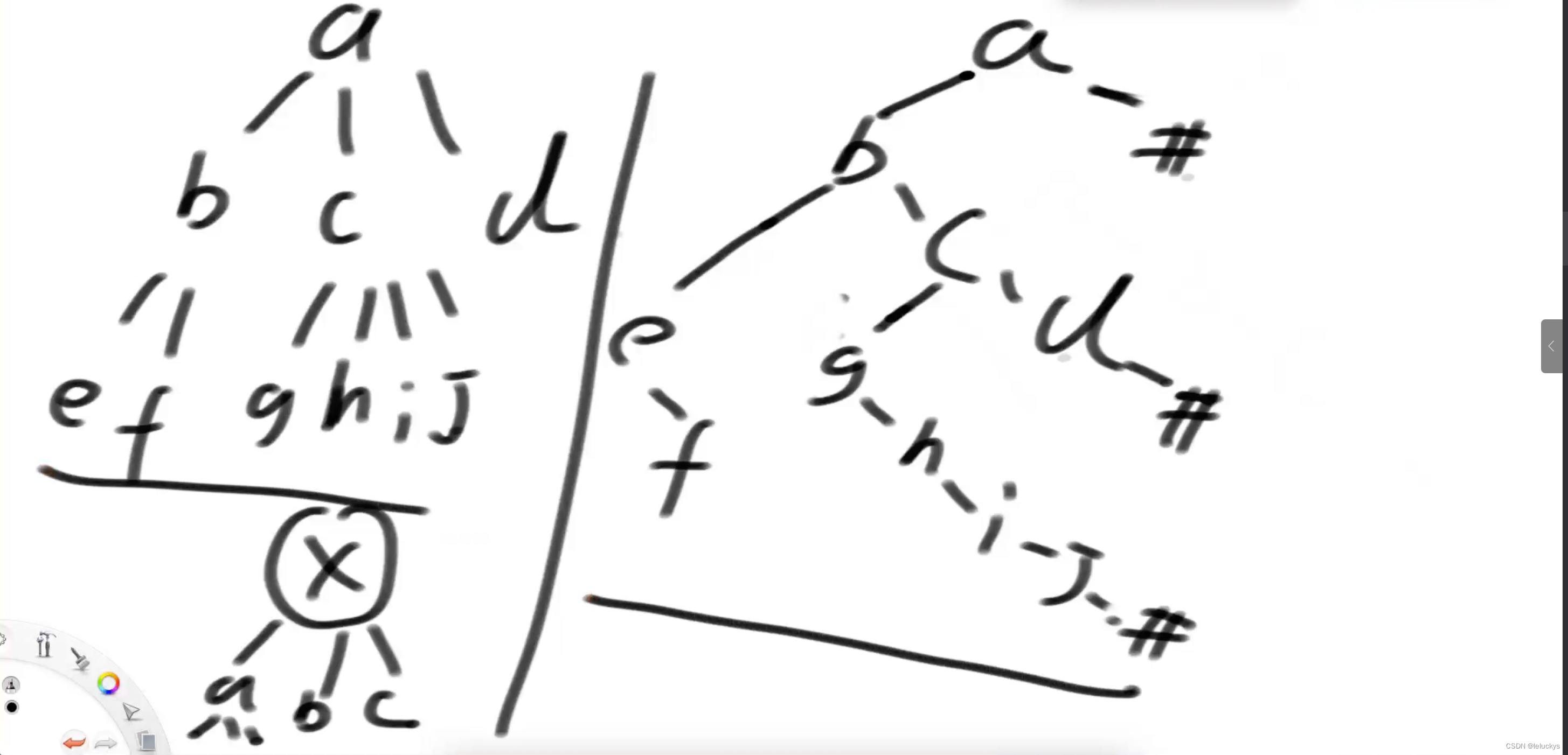
3.3 代码

package class11;

import java.util.ArrayList;
import java.util.List;

// 本题测试链接：https://leetcode.com/problems/encode-n-ary-tree-to-binary-tree
public class Code03_EncodeNaryTreeToBinaryTree {

    // 提交时不要提交这个类
    public static class Node {
        public int val;
        public List<Node> children;

        public Node() {
        }

        public Node(int _val) {
            val = _val;
        }

        public Node(int _val, List<Node> _children) {
            val = _val;
            children = _children;
        }
    };

    // 提交时不要提交这个类
    public static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode(int x) {
            val = x;
        }
    }

    // 只提交这个类即可
    class Codec {
        // Encodes an n-ary tree to a binary tree.
        public TreeNode encode(Node root) {
            if (root == null) {
                return null;
            }
            TreeNode head = new TreeNode(root.val);
            head.left = en(root.children);
            return head;
        }

        private TreeNode en(List<Node> children) {
            TreeNode head = null;
            TreeNode cur = null;
            for (Node child : children) {
                TreeNode tNode = new TreeNode(child.val);
                if (head == null) {
                    head = tNode;
                } else {
                    cur.right = tNode;
                }
                cur = tNode;
                cur.left = en(child.children);
            }
            return head;
        }

        // Decodes your binary tree to an n-ary tree.
        public Node decode(TreeNode root) {
            if (root == null) {
                return null;
            }
            return new Node(root.val, de(root.left));
        }

        public List<Node> de(TreeNode root) {
            List<Node> children = new ArrayList<>();
            while (root != null) {
                Node cur = new Node(root.val, de(root.left));
                children.add(cur);
                root = root.right;
            }
            return children;
        }

    }

}

四求二叉树最宽的层有多少个节点

4.1 描述

打印二叉树每层的的节点树及最多的节点数；

4.2 分析

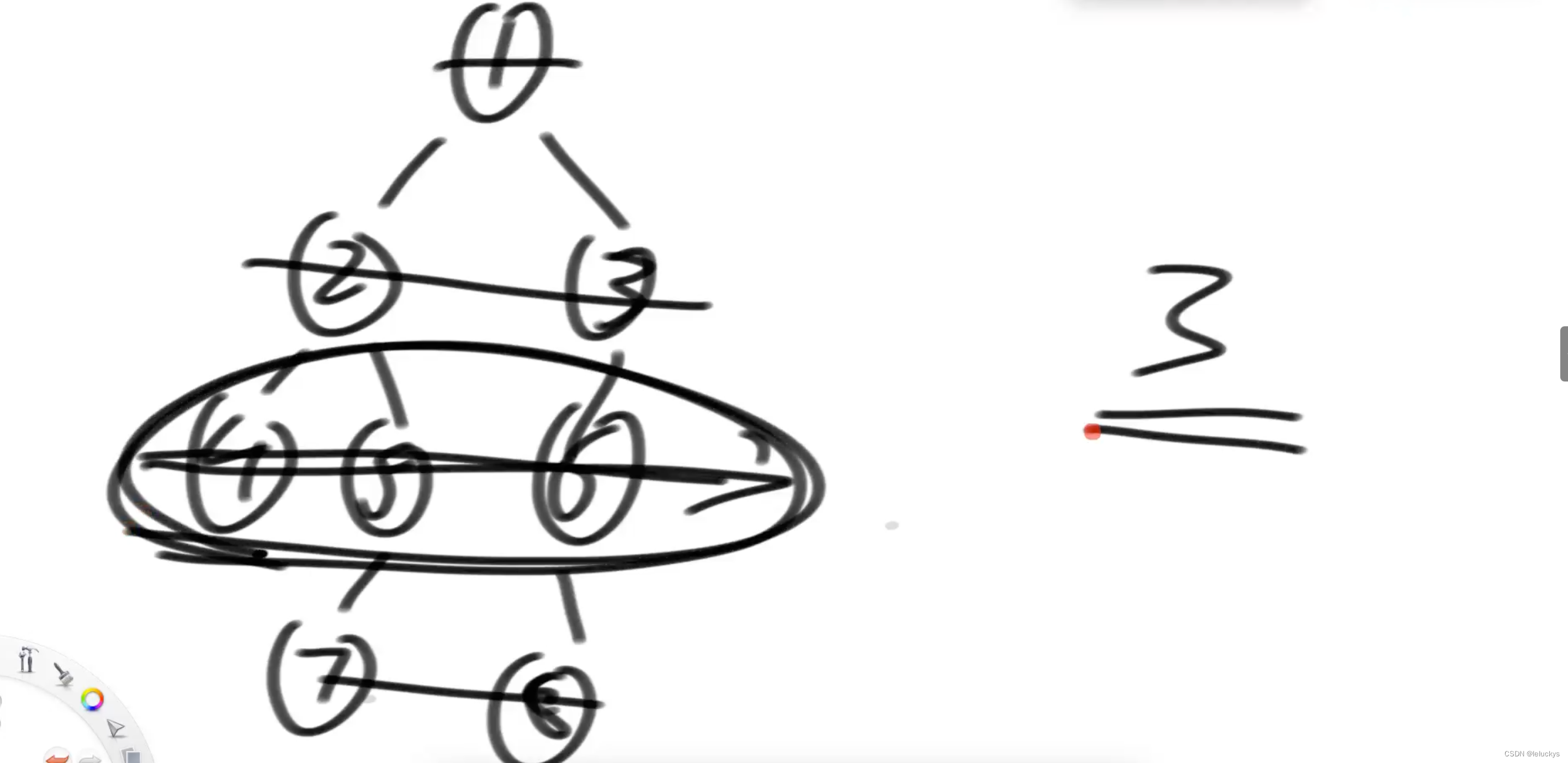
根据宽度优先遍历的基础上，要是能知道哪一层结束，那么就能算出每一层的节点数；

设计两个数，Node curEnd = head; // 当前层，最右节点是谁Node nextEnd = null; // 下一层，最右节点是谁

每次遍历当前节点时候，判断该节点是否和记录的curEnd节点相等，相等就是当前层结束了，把当前层的节点数更新到max中，

再将当前节点的每一个左右孩子更新到队列中的过程中，每一步都更新nextEnd的值为当前加队列的值，下一层遍历来的时候更新curEnd值为nextEnd

4.3 代码

public static int maxWidthNoMap(Node head) {
        if (head == null) {
            return 0;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.add(head);
        Node curEnd = head; // 当前层，最右节点是谁
        Node nextEnd = null; // 下一层的最右节点是谁。提前为下一层出来的end节点做准备
        int max = 0;
        int curLevelNodes = 0; // 当前层的节点数
        while (!queue.isEmpty()) {
            Node cur = queue.poll();
            if (cur.left != null) {
                queue.add(cur.left);
                nextEnd = cur.left;
            }
            if (cur.right != null) {
                queue.add(cur.right);
                nextEnd = cur.right;
            }
            curLevelNodes++;
            if (cur == curEnd) {
                max = Math.max(max, curLevelNodes);
                curLevelNodes = 0;
                curEnd = nextEnd;
            }
        }
        return max;
    }
 
 
 
 //使用额外HashMapd
 public static class Node {
        public int value;
        public Node left;
        public Node right;

        public Node(int data) {
            this.value = data;
        }
    }

    public static int maxWidthUseMap(Node head) {
        if (head == null) {
            return 0;
        }
        Queue<Node> queue = new LinkedList<>();
        queue.add(head);
        // key 在 哪一层，value
        HashMap<Node, Integer> levelMap = new HashMap<>();
        levelMap.put(head, 1);
        int curLevel = 1; // 当前你正在统计哪一层的宽度
        int curLevelNodes = 0; // 当前层curLevel层，宽度目前是多少
        int max = 0;
        while (!queue.isEmpty()) {
            Node cur = queue.poll();
            int curNodeLevel = levelMap.get(cur);
            if (cur.left != null) {
                levelMap.put(cur.left, curNodeLevel + 1);
                queue.add(cur.left);
            }
            if (cur.right != null) {
                levelMap.put(cur.right, curNodeLevel + 1);
                queue.add(cur.right);
            }
            if (curNodeLevel == curLevel) {
                curLevelNodes++;
            } else {
                max = Math.max(max, curLevelNodes);
                curLevel++;
                curLevelNodes = 1;
            }
        }
        max = Math.max(max, curLevelNodes);
        return max;
    }

五二叉树中的某个节点，返回该节点的后继节点

5.1 描述

后继节点：比如中序遍历，求该节点的4的后继节点，就是中序遍历遍历到该节点后的所有节点

二叉树结构如下定义：

Class Node {

V value;

Node left;

Node right;

Node parent;

}

给你二叉树中的某个节点，返回该节点的后继节点

5.2 分析中序遍历

5.2.1 方案一先通过parrent 找到的他的跟节点后，然后通root找到他的中序遍历，然后就可以找到该节点的后继节点

方案二

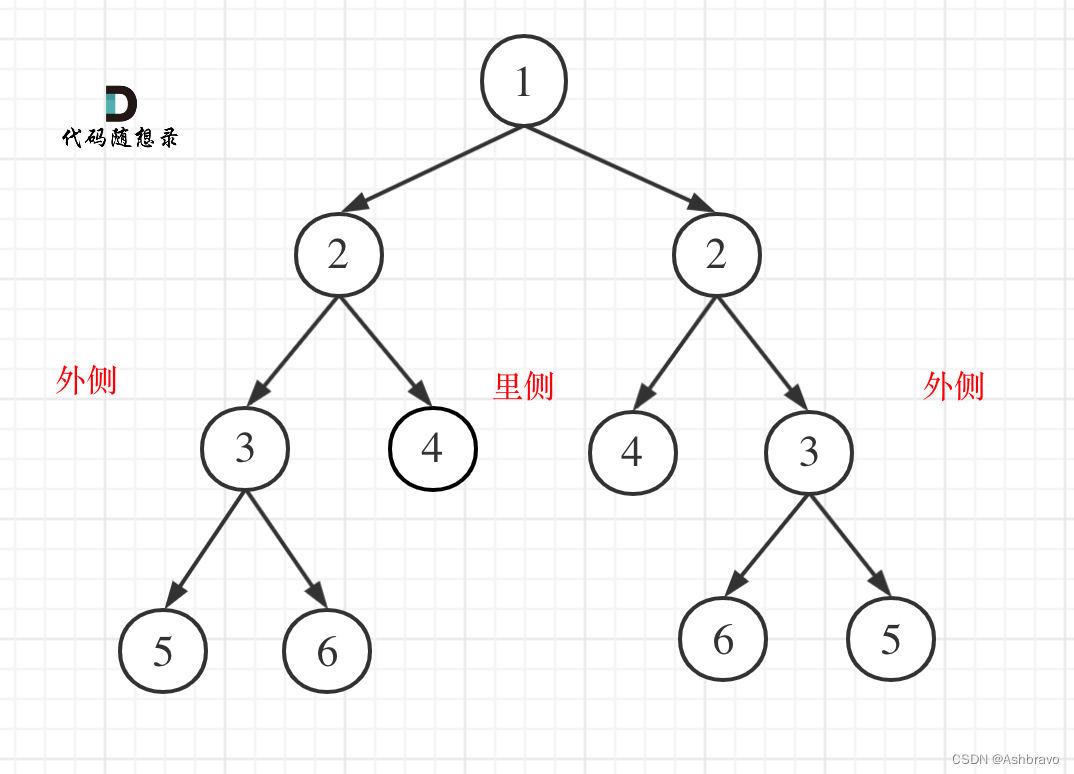
5.2.2 情况1一如果该节点有右数，那么他的后继节点一定是他右树的最左侧节点

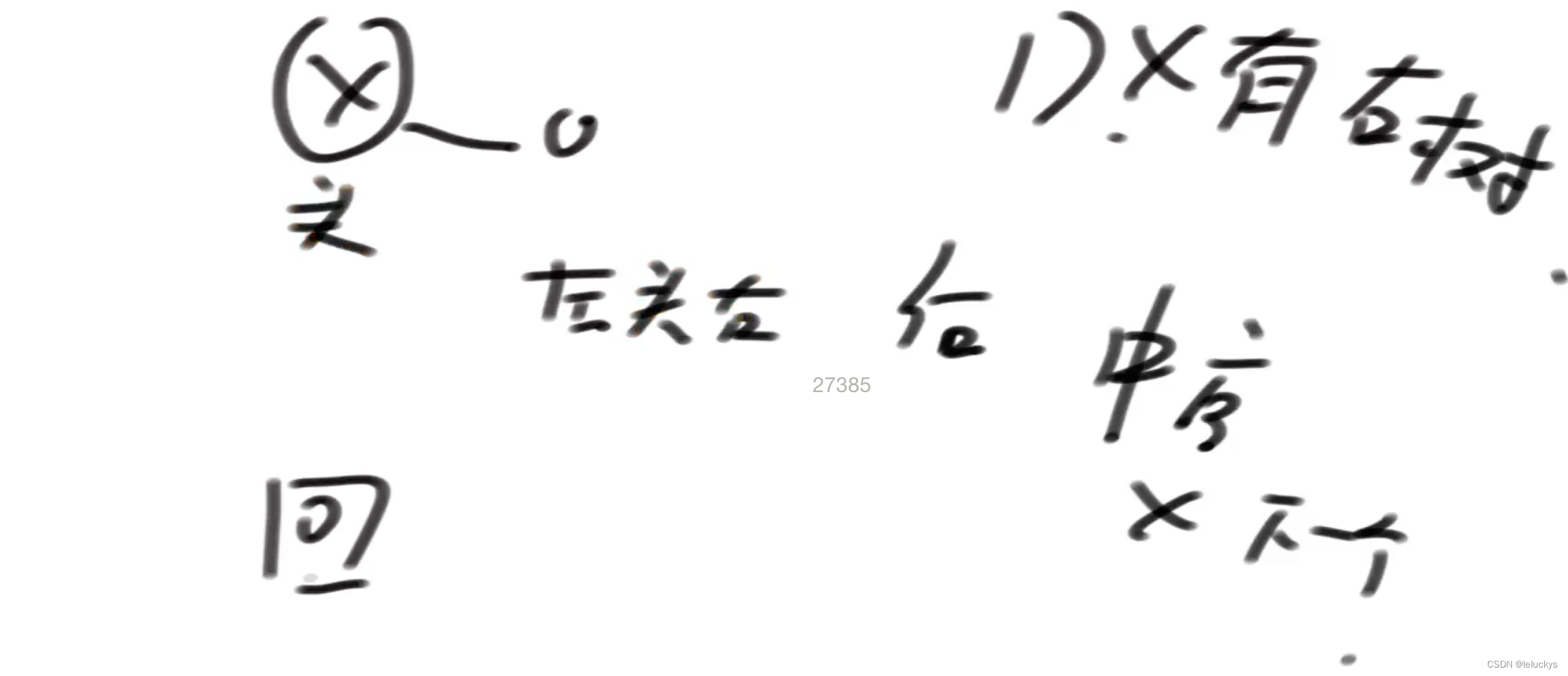
情况二当该节点没有右树的时候，去找该节点是谁的节点左树的最右侧节点（中序遍历的本质理解）如果没有右子树，根据中序遍历的特点，下一个就应该是去找该节点是谁的节点左树的最右侧节点

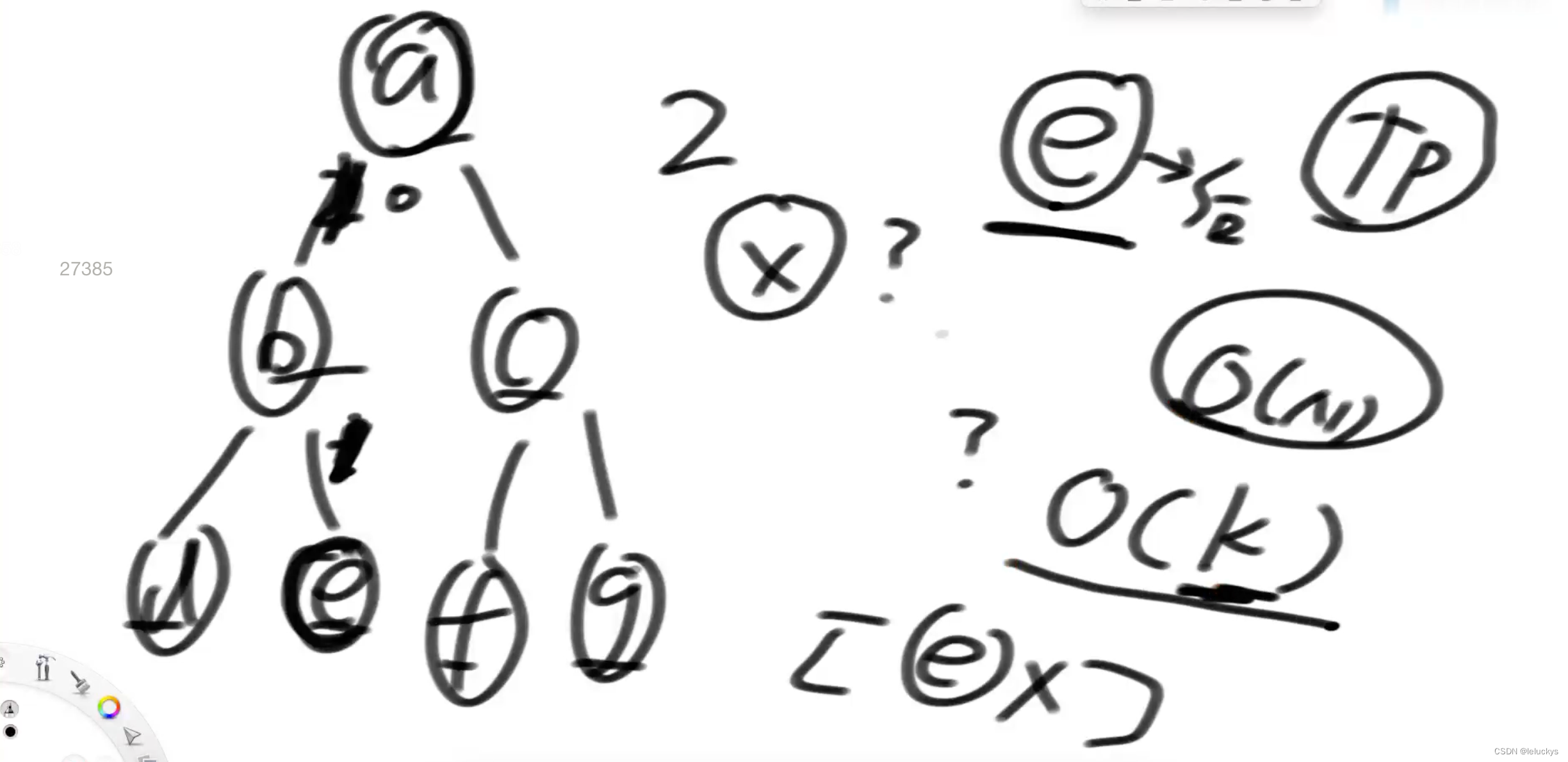
情况二讨论如下找一个数的后继节点，一直往上找，通过找到该节点的最后一个父节点，该节点的右子树就是他的后继节点

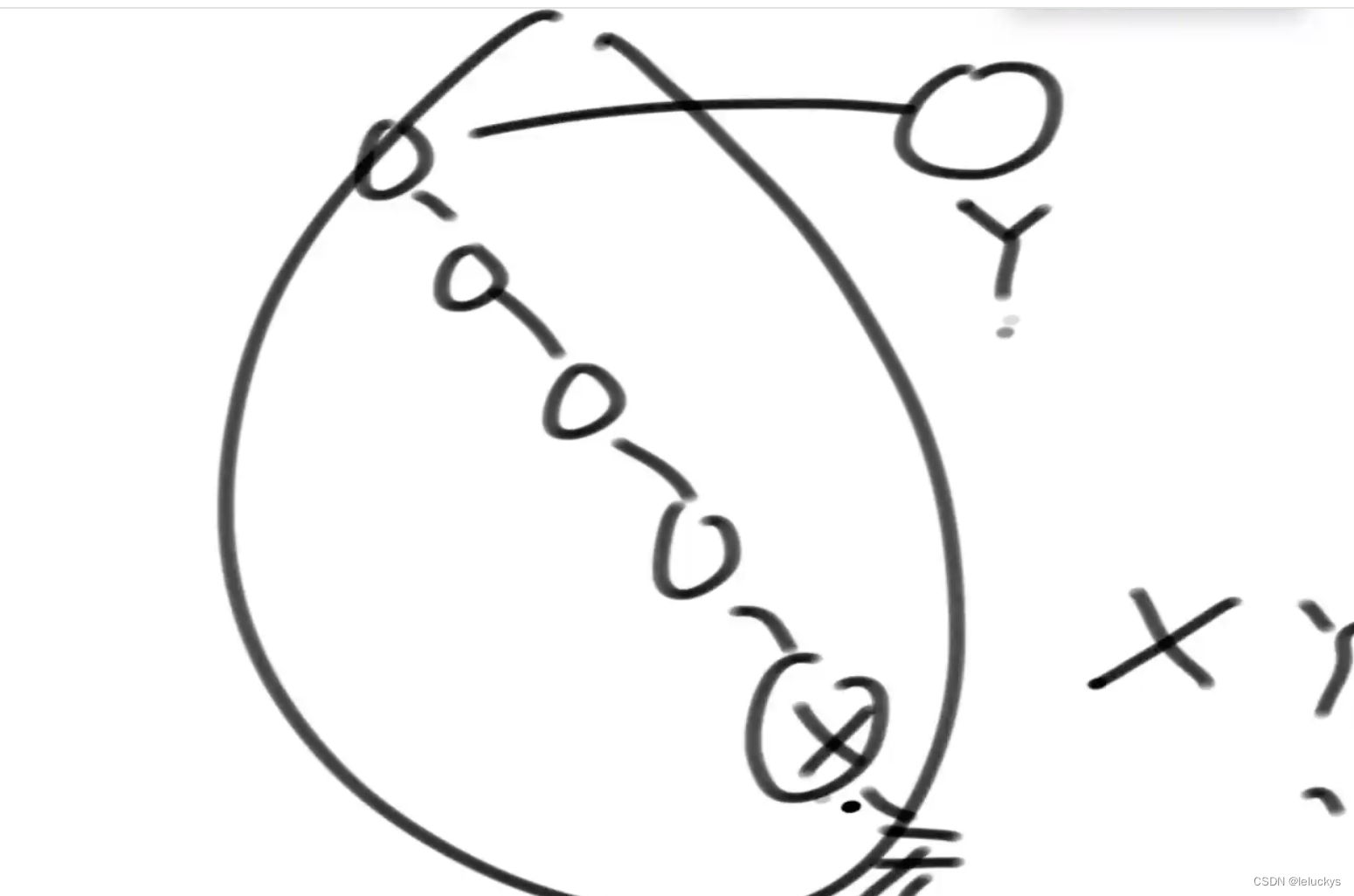
如下，x是y左数的最右节点，所以打印完x就该打印y了 == 找的就是那个左树上的最右节点

5.3 代码

public class Code06_SuccessorNode {

    public static class Node {
        public int value;
        public Node left;
        public Node right;
        public Node parent;

        public Node(int data) {
            this.value = data;
        }
    }

    public static Node getSuccessorNode(Node node) {
        if (node == null) {
            return node;
        }
        if (node.right != null) {
            return getLeftMost(node.right);
        } else { // 无右子树
            Node parent = node.parent;
            while (parent != null && parent.right == node) { // 当前节点是其父亲节点右孩子
                node = parent;
                parent = node.parent;
            }
            return parent;
        }
    }

    public static Node getLeftMost(Node node) {
        if (node == null) {
            return node;
        }
        while (node.left != null) {
            node = node.left;
        }
        return node;
    }