5.3. 二叉树的遍历和线索二叉树
5.3.1_1 二叉树的先中后序遍历
遍历:按照某种次序把所有结点都访问一遍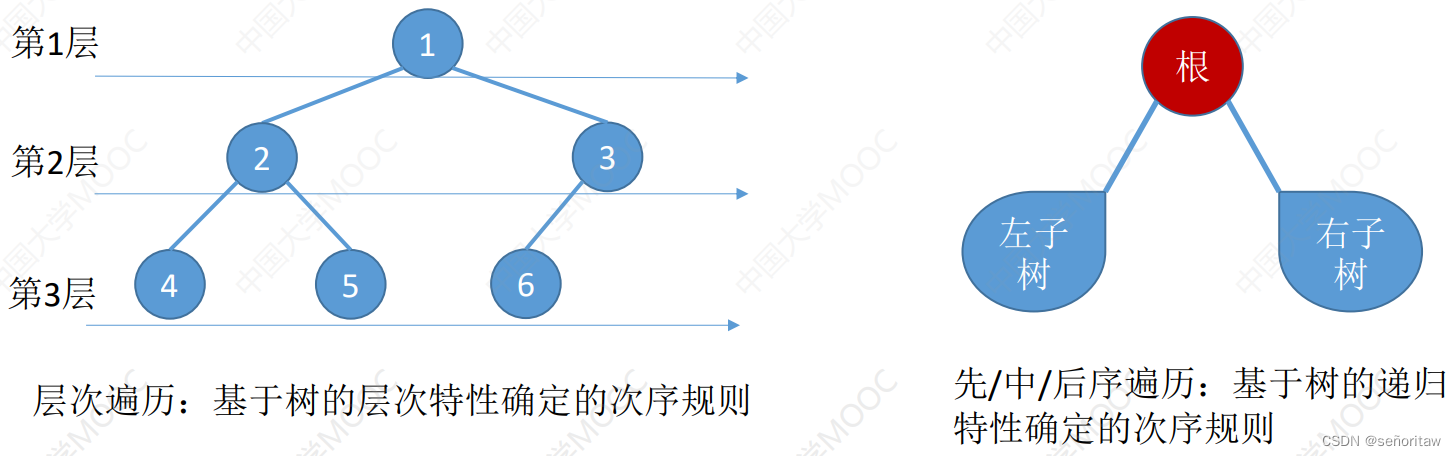
二叉树的递归特性:
①要么是个空二叉树
②要么就是由“根节点+左子树+右子树”组成的二叉树
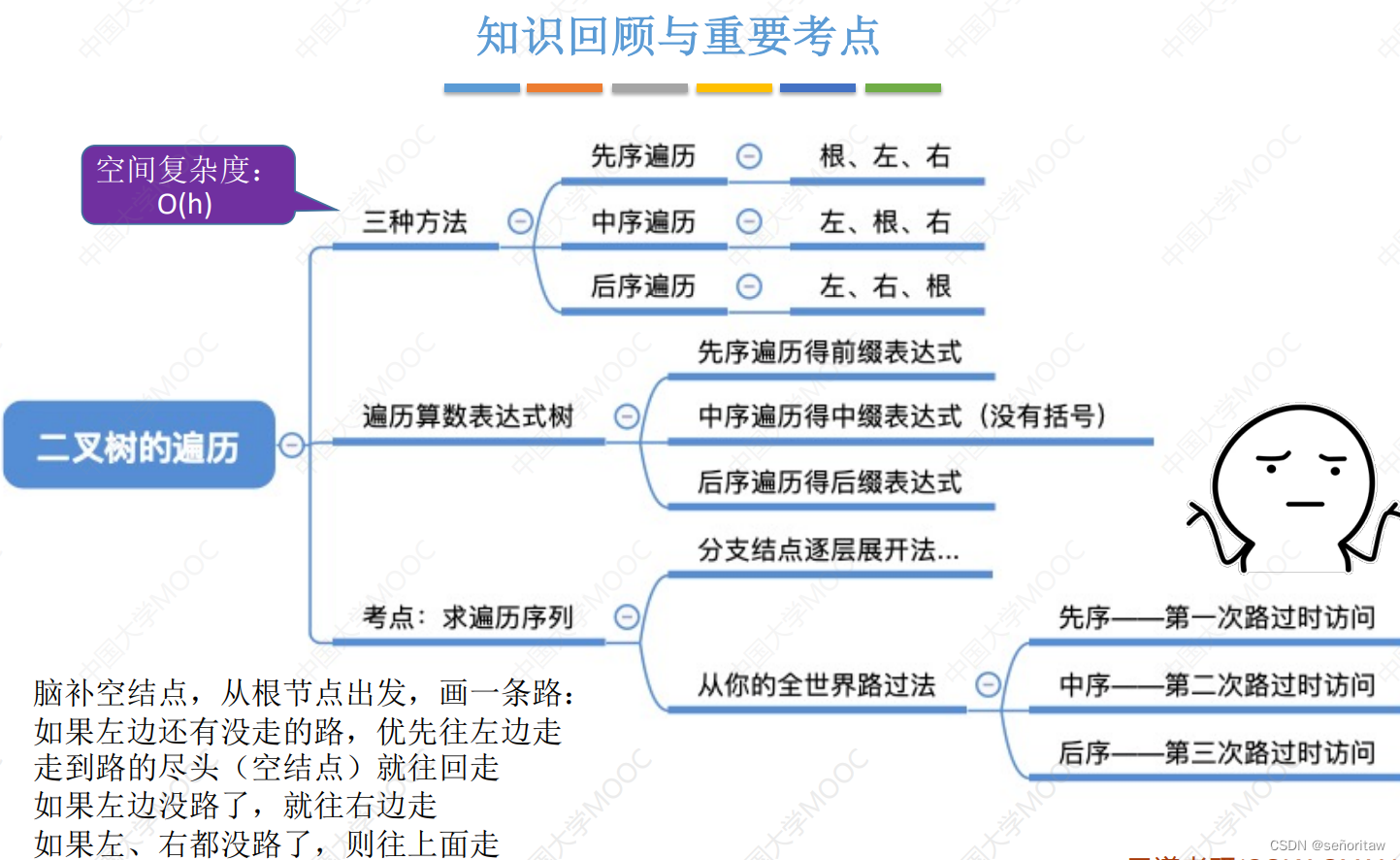
先序遍历:根左右(NLR)
中序遍历:左根右(LNR)
后序遍历:左右根(LRN)

先序遍历(PreOrder)的操作过程如下:
1. 若二叉树为空,则什么也不做;
2. 若二叉树非空:
①访问根结点;
②先序遍历左子树;
③先序遍历右子树。
代码实现如下:
typedef struct BiTNode{
ElemType data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
// 先序遍历
void PreOrder(BiTree T){
if(T!=NULL){
visit(T); //访问根结点
PreOrder(T->lchild); //递归遍历左子树
PreOrder(T->rchild); //递归遍历右子树
}
}
先序遍历—第一次路过时访问结点,图示如下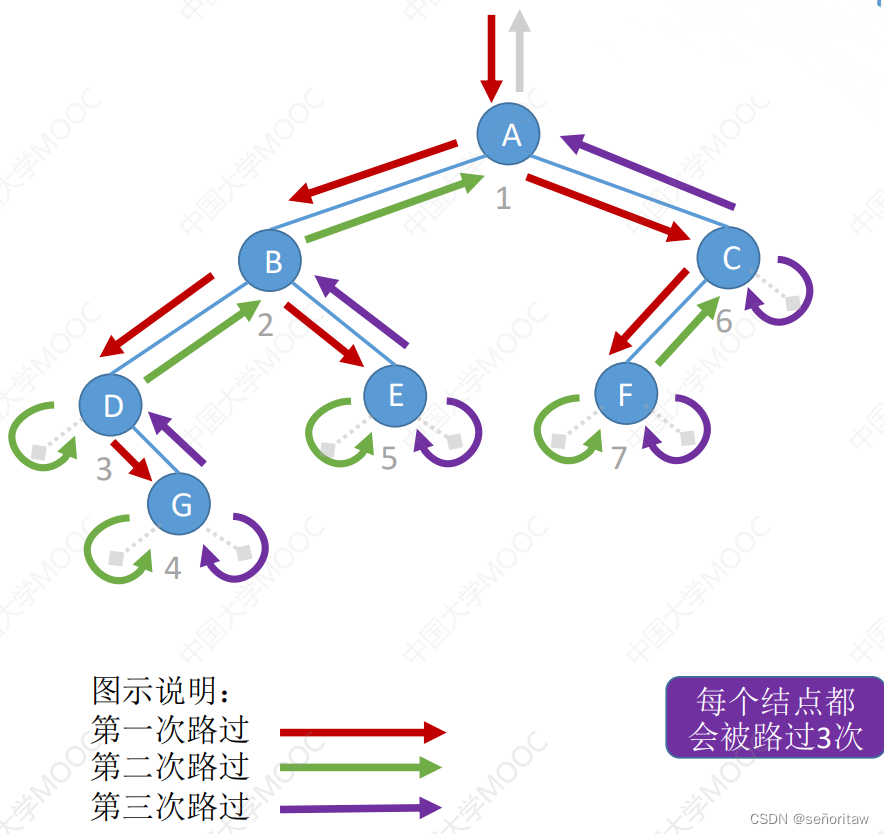
中序遍历(InOrder)的操作过程如下:
1. 若二叉树为空,则什么也不做;
2. 若二叉树非空:
①中序遍历左子树;
②访问根结点;
③中序遍历右子树;
代码实现如下:
typedef struct BiTNode{
ElemType data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
// 中序遍历
void PreOrder(BiTree T){
if(T!=NULL){
PreOrder(T->lchild); //递归遍历左子树
visit(T); //访问根结点
PreOrder(T->rchild); //递归遍历右子树
}
}
中序遍历—第二次路过时访问结点,图示如下
后序遍历(InOrder)的操作过程如下:
1. 若二叉树为空,则什么也不做;
2. 若二叉树非空:
①后序遍历左子树;
②后序遍历右子树;
③访问根结点。
代码实现如下:
typedef struct BiTNode{
ElemType data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
// 后序遍历
void PreOrder(BiTree T){
if(T!=NULL){
PreOrder(T->lchild); //递归遍历左子树
PreOrder(T->rchild); //递归遍历右子树
visit(T); //访问根结点
}
}
后序遍历—第三次路过时访问结点 ,图示如下
// 应用:求树的深度
int treeDepth(BiTree T){
if(T == NULL){
return 0;
}else{
int l = treeDepth(T->lchild);
int r = treeDepth(T->rchild);
//树的深度=Max(左子树深度,右子树深度)+1
return l>r ? l+1 r+1;
}
}
5.3.1_2 二叉树的层次遍历
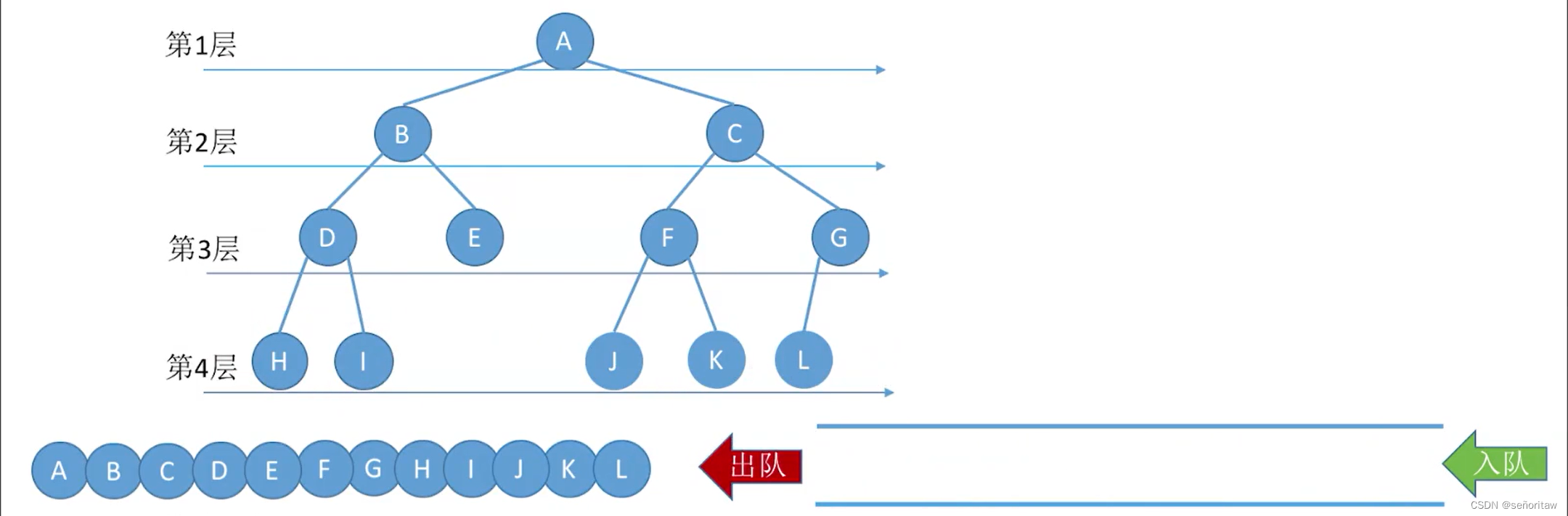
算法思想:
①初始化一个辅助队列
②根结点入队
③若队列非空,则队头结点出队,访问该结点,并将其左、右孩子插入队尾(如果有的话)
④重复③直至队列为空
代码实现:
// 二叉树结点(链式存储)
typedef struct BiTNode{
char data;
struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
// 链式队列结点
typedef struct LinkNode{
BiTNode *data; //存结点的指针而不是结点本身
struct LinkNode *next;
}LinkNode;
typedef struct{
LinkNode *front, *rear; //队头队尾
}LinkQueue;
// 层序遍历
void LevelOrder(BiTree T){
LinkQueue Q;
InitQueue(Q); //初始化辅助队列
BiTree p;
EnQueue(Q, T); //将根结点入队
while(!IsEmpty(Q)){ //队列不空则循环
DeQueue(Q, p); //队头结点出队
visit(p); //访问出队结点
if(p->lchild!=NULL)
EnQueue(Q, p->lchild); //左孩子入队
if(p->rchild!=NULL)
EnQueue(Q, p->rchild); //右孩子入队
}
}
5.3.1_3 由遍历序列构造二叉树
若只给出一棵二叉树的 前/中/后/层 序遍历序列中的一种,不能唯一确定一棵二叉树
一种遍历序列可能对应多种形态



前序 + 中序遍历序列
由前序遍历可推出根节点在中序遍历中的位置,从而确定左右结点,再依此类推
后序 + 中序遍历序列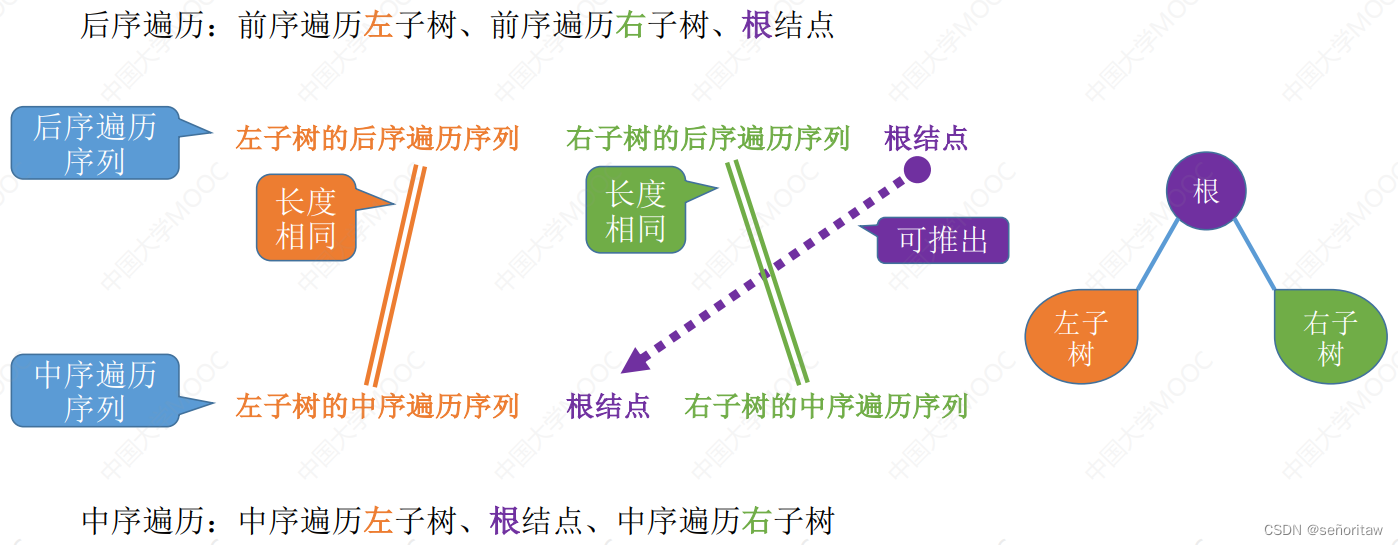
由后序遍历可推出根结点在中序遍历中的位置,从而确定左右结点在中序遍历的位置
层序 + 中序遍历序列
由层序遍历可推出根结点,再根据根节点进一步确定左右的根的位置
5.3.2_1 线索二叉树的概念
普通二叉树进行遍历时,找前驱、后继很不方便,且每次都要从根结点出发,无法从一个指定的结点开始遍历。
n 个结点的二叉树,有 n+1 个空链域,可用来记录前驱、后继的信息。
指向前驱、后继的指针被称为“线索”,形成的二叉树就称为线索二叉树。

线索二叉树的存储
线索二叉树的结点在原本二叉树的基础上,新增了左右线索标志 tag。
tag == 0 时,表示指针指向孩子;tag == 1 时,表示指针是“线索”。
// 线索二叉树的结点
typedef struct ThreadNode{
ElemType data;
struct ThreadNode *lchild, *rchild;
int ltag, rtag; //左、右线索标志
}ThreadNode,*ThreadTree;
中序线索二叉树的存储
先序线索二叉树



5.3.2_2 二叉树的线索化
中序线索化
//线索二叉树结点
typedef struct ThreadNode{
ElemType data;
struct ThreadNode *lchild, *rchild;
int ltag, rtag; //左、右线索标志
}ThreadNode, *ThreadTree;
// 中序遍历二叉树,一边遍历一边线索化
void InThread(ThreadTree T) {
if (T != NULL) {
InThread(p->lchild); //中序遍历左子树
visit(T); //访问根结点
InThread(p->rchild); //中序遍历右子树
}
}
void visit(ThreadNode *q) {
if(q->lchild==NULL){ //左子树为空,建立前驱线索
q->lchild=pre; //
q->ltag=1; //修改ltag=1,只有变成1才表示指针是线索
}
if(pre!=NULL&&pre->rchild==NULL){
pre->rchild=q; //建立前驱结点的后继线索
pre->rtag=1;
}
pre=q;
}
//全局变量pre,指向当前访问结点的前驱
ThreadNode *pre=NULL; //pre没有前驱,最开始指向NULL
// 中序化线索二叉树T
void CreateInThread(ThreadTree T) {
pre = NULL; //pre初始化为NULL
if (T != NULL) { //非空二叉树才能线索化
InThread(T, pre); //中序化线索二叉树
if(pre->rchild = NULL)
pre->rtag = 1; //处理遍历的最后一个结点
}
}
先序线索化
// 先序遍历二叉树T
void PreThread(ThreadTree T) {
if (T != NULL) { //非空二叉树才能线索化
visit(T); //先处理根结点
if(T->ltag ==0) //lchild不是前驱线索
PreThread(T->child);
PreThread(T->child);
}
}
void visit(ThreadNode *q) {
if(q->lchild==NULL){ //左子树为空,建立前驱线索
q->lchild=pre; //
q->ltag=1; //修改ltag=1,只有变成1才表示指针是线索
}
if(pre!=NULL&&pre->rchild==NULL){
pre->rchild=q; //建立前驱结点的后继线索
pre->rtag=1;
}
pre=q;
}
//全局变量pre,指向当前访问结点的前驱
ThreadNode *pre=NULL; //pre没有前驱,最开始指向NULL
void CreateInThread(ThreadTree T) {
pre = NULL; //pre初始化为NULL
if (T != NULL) { //非空二叉树才能线索化
PreThread(T); //先序化线索二叉树
if(pre->rchild = NULL)
pre->rtag = 1; //处理遍历的最后一个结点
}
}
后序线索化
// 后序遍历二叉树T
void PostThread(ThreadTree T) {
if (T != NULL) { //非空二叉树才能线索化
PreThread(T->child); //后序遍历左子树
PreThread(T->child); //后序遍历右子树
visit(T); //访问根结点
}
}
void visit(ThreadNode *q) {
if(q->lchild==NULL){ //左子树为空,建立前驱线索
q->lchild=pre; //
q->ltag=1; //修改ltag=1,只有变成1才表示指针是线索
}
if(pre!=NULL&&pre->rchild==NULL){
pre->rchild=q; //建立前驱结点的后继线索
pre->rtag=1;
}
pre=q;
}
//全局变量pre,指向当前访问结点的前驱
ThreadNode *pre=NULL; //pre没有前驱,最开始指向NULL
//后续线索化二叉树T
void CreateInThread(ThreadTree T) {
pre = NULL; //pre初始化为NULL
if (T != NULL) { //非空二叉树才能线索化
PostThread(T); //后续线索化二叉树
if(pre->rchild = NULL)
pre->rtag = 1; //处理遍历的最后一个结点
}
}

5.3.2_3 在线索二叉树中找前驱后继
在中序线索二叉树中找到指定结点*p 的中序后继 next
①若 p->rtag==1,则 next = p->rchild
②若 p->rtag==0,则 next = p 的右子树中最左下结点
// 找到以p为根的子树中,第一个被中序遍历的结点
ThreadNode *FirstNode(ThreadNode *p){
// 循环找到最左下结点(不一定是叶结点)
while(p->ltag==0)
p=p->rchild;
return p;
}
// 在中序线索二叉树中找到结点p的后继结点
ThreadNode *NextNode(ThreadNode *p){
// 右子树中最左下的结点
if(p->rtag==0)
return FirstNode(p->lchild);
else
return p->rchild; //rtage==1直接返回后继线索
}
// 对中序线索二叉树进行中序循环(利用线索实现的非递归方法) 空间复杂度O(1)
void InOrder(ThreadNode *T){
for(ThreadNode *p=FirstNode(T); p!=NULL; p=NextNode(p))
visit(p);
}
在中序线索二叉树中找到指定结点*p 的中序前驱 pre
①若 p->ltag==1,则 pre = p->lchild
②若 p->ltag==0
// 找到以p为根的子树中,最后一个被中序遍历的结点
ThreadNode *LastNode(ThreadNode *p){
// 循环找到最右下结点(不一定是叶结点)
while(p->rtag==0)
p=p->rchild;
return p;
}
// 在中序线索二叉树中找到结点p的前驱结点
ThreadNode *PreNode(ThreadNode *p){
// 左子树中最右下的结点
if(p->ltag==0)
return LastNode(p->lchild);
else
return p->lchild; //ltage==1直接返回前驱线索
}
// 对中序线索二叉树进行中序循环(非递归方法实现)
void RevOrder(ThreadNode *T){
for(ThreadNode *p=LastNode(T); p!=NULL; p=PreNode(p))
visit(p);
}
在先序线索二叉树中找到指定结点*p 的先序后继 next
①若 p->rtag==1,则 next = p->rchild
②若 p->rtag==0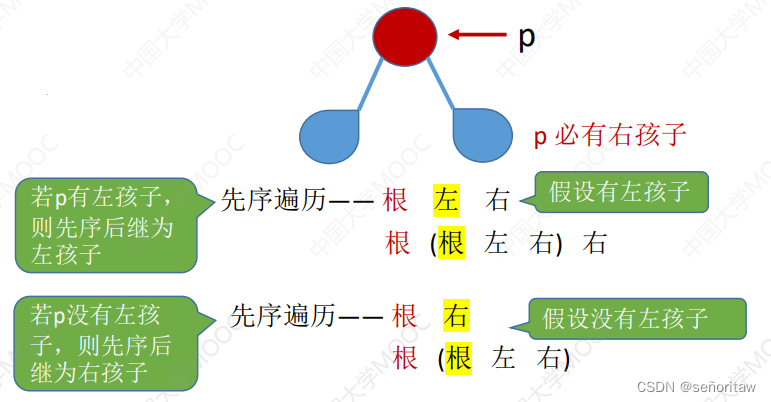
在先序线索二叉树中找到指定结点*p 的先序前驱 pre
①若 p->ltag==1,则 next = p->lchild
②若 p->ltag==0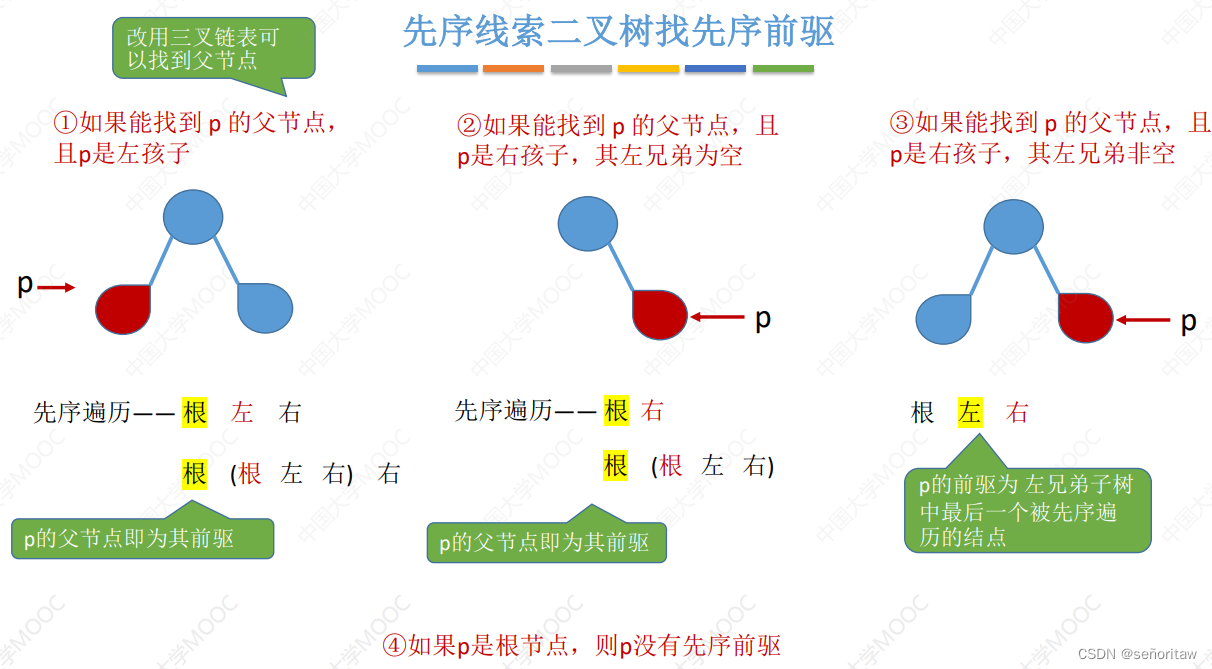
在后序线索二叉树中找到指定结点*p 的后序前驱 pre
①若 p->ltag==1,则 pre = p->lchild
②若 p->ltag==0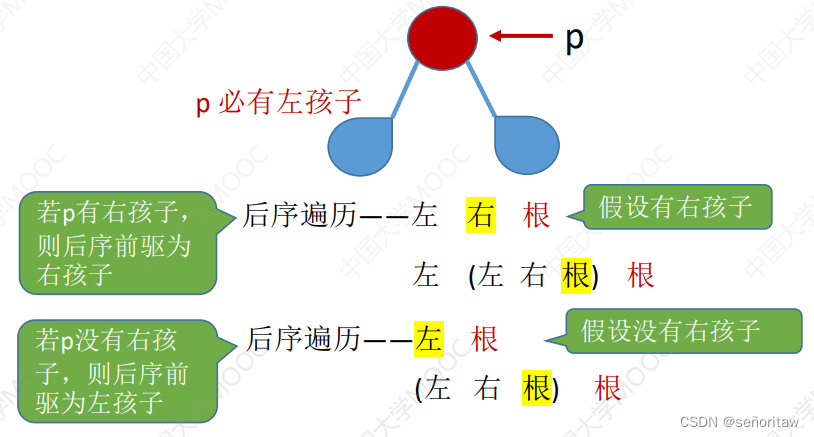
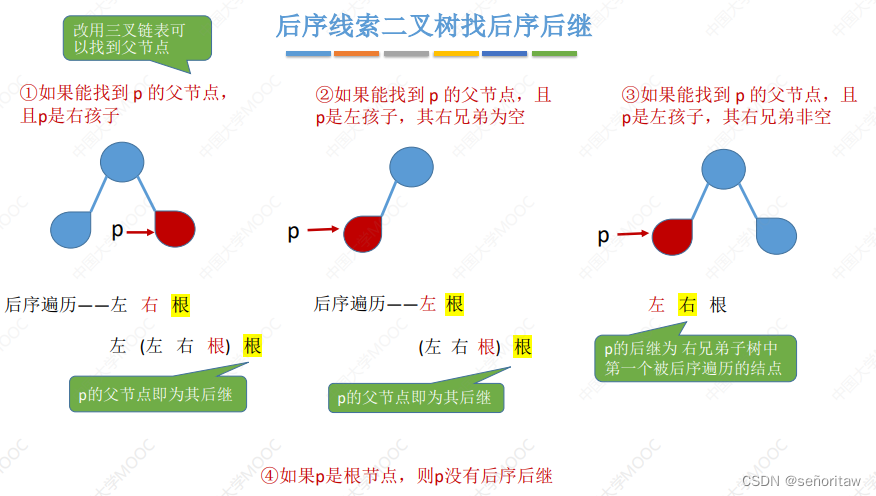
在后序线索二叉树中找到指定结点*p 的后序后继 next
①若 p->rtag==1,则 next = p->rchild
②若 p->rtag==0