回溯
从今天开始进入回溯,其实此前也接触过几道使用了该思想的题目
回溯的思想是“倒退到上一个状态”,通常结合递归,解决的问题多是“从众多组合中找出符合条件的组合”的问题,随想录中给出了题目大纲:
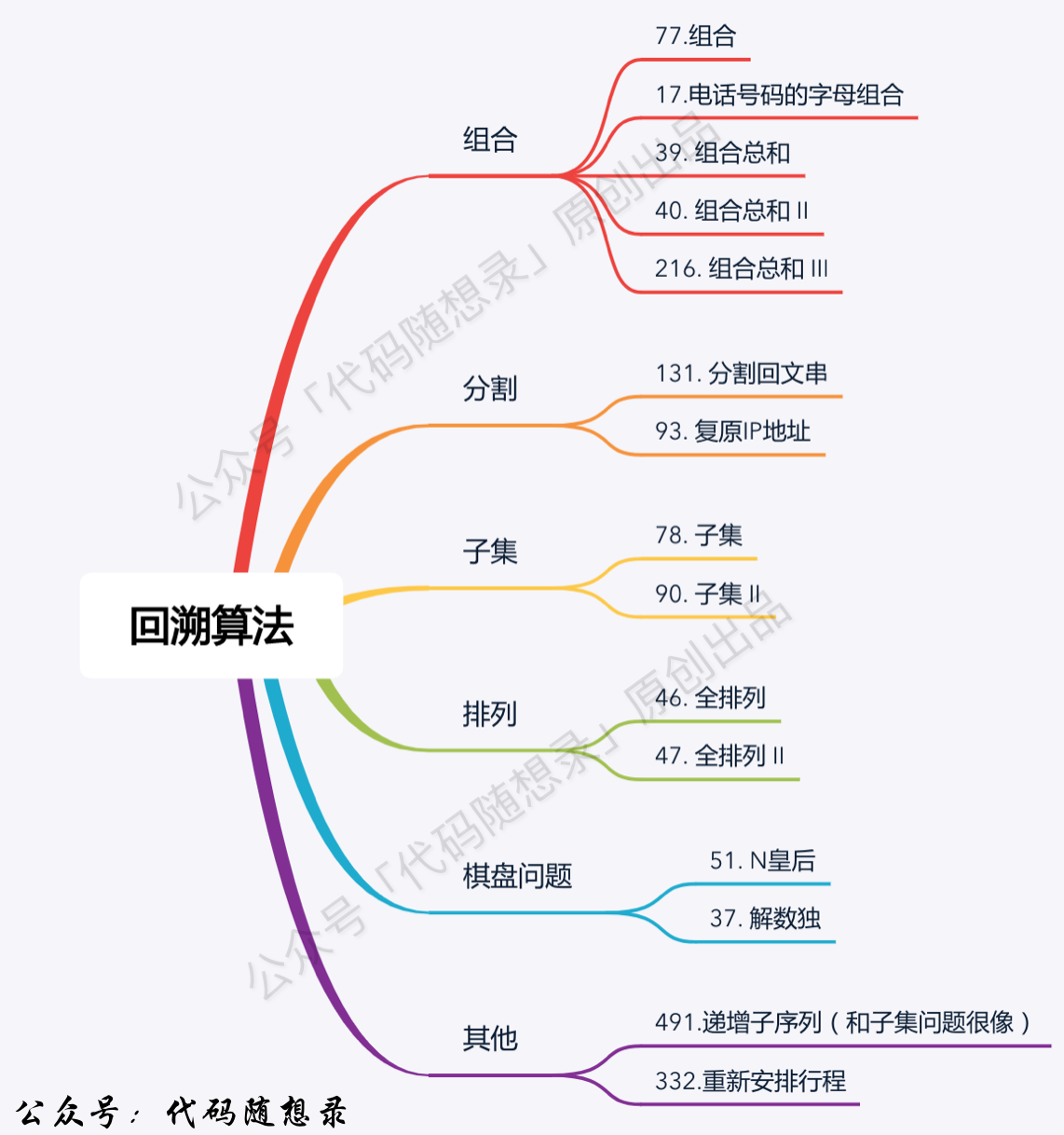
回溯算法解决的问题可以抽象为树形结构,深度和广度决定了回溯算法遍历的次数,也可以近似递归,分为“函数返回类型 + 传入参数”、“终止条件”、“单层递归逻辑”三步。
77 组合 medium
给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。
只看题目,我们首先能想到的方法应该是暴力搜索,执行k个循环,但是暴力搜索带来的问题就是随着k的增大,时间复杂度会极高。
于是,为了以空间换时间,我们定义两个数组,一个用于存放所有组合,为我们最终的返回结果;另一个则用于记录k个数。
另外,为了避免已经遍历过的数不被重复遍历,我们需要一个参数,来限制每次回溯过程中的起始位置;
回溯结束的条件是数组中已经有了k个数;
每次回溯前,把当前结点添加入组成k个数的数组中,回溯后,再把当前结点删除,整体代码如下:
vector<vector<int>> res;
vector<int> path;
void reback (int n, int k, int startIndex) {
if (path.size() == k) {
res.push_back(path);
return;
}
for (int i = startIndex; i <= n; ++i) {
path.push_back(i);
reback(n, k, i + 1);
path.pop_back();
}
return;
}
vector<vector<int>> combine(int n, int k) {
if (n == 0 || k == 0) return {};
reback(n, k, 1);
return res;
}
这道题还有可以优化的空间。因为如果剩余的数字,不够组合成k个数字,那就没必要再遍历了。随想录中给出了一个极端的例子,n = 4, k = 4,只需要遍历一次就可以了,没必要让 i 从1一直增加到4;
再举个例子,就是n = 4, k = 3,当 i = 2时,算上2只剩下234三个数字,所有组合就已经可以遍历完了。根据当前回溯的起始位置startIndex和遍历总数n,来进行剪枝
- 已经选择的元素个数:path.size();
- 所需需要的元素个数为: k - path.size();
- 列表中剩余元素(n-i) >= 所需需要的元素个数(k - path.size())
- 在集合n中至多要从该起始位置 : i <= n - (k - path.size()) + 1,开始遍历
为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。
举个例子,n = 4,k = 3, 目前已经选取的元素为0(path.size为0),n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。
所以,给出优化版本,代码如下:
vector<vector<int>> res;
vector<int> path;
void reback (int n, int k, int startIndex) {
if (path.size() == k) {
res.push_back(path);
return;
}
for (int i = startIndex; i <= n - (k - path.size()) + 1; ++i) {
path.push_back(i);
reback(n, k, i + 1);
path.pop_back();
}
return;
}
vector<vector<int>> combine(int n, int k) {
if (n == 0 || k == 0) return {};
reback(n, k, 1);
return res;
}
216 组合总和III medium
找出所有相加之和为 n 的 k 个数的组合,且满足下列条件:
只使用数字1到9
每个数字 最多使用一次
返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次,组合可以以任何顺序返回。
这道题相比较于上一道题,区别在于求和,只需要在传入参数中添加当前和,并在终止条件中判断,当前和是否等于目标和,而且候选数组大小等于k。
本题代码如下:
vector<vector<int>> res;
vector<int> path;
void reback (int k, int n, int startIndex, int sum) {
if (sum == n && path.size() == k) {
res.push_back(path);
return;
}
for (int i = startIndex; i <= 9; ++i) {
path.push_back(i);
reback(k, n, i + 1, sum + i);
path.pop_back();
}
return;
}
vector<vector<int>> combinationSum3(int k, int n) {
reback(k, n, 1, 0);
return res;
}
这道题也可以进行剪枝,剪枝操作根据当前的起始点和与目标值的差值来判断,即:
如果当前元素总和已经大于目标值了,就没必要往下遍历了
在终止条件前,加一个判断语句就可以了,代码如下:
vector<vector<int>> res;
vector<int> path;
void reback (int k, int n, int startIndex, int sum) {
if (sum > n) return;
if (sum == n && path.size() == k) {
res.push_back(path);
return;
}
for (int i = startIndex; i <= 9; ++i) {
path.push_back(i);
reback(k, n, i + 1, sum + i);
path.pop_back();
}
return;
}
vector<vector<int>> combinationSum3(int k, int n) {
reback(k, n, 1, 0);
return res;
}