目录
1、网络分析(第十一届蓝桥杯省赛第一场C++ A组/B组)
2、奶酪(NOIP2017提高组)
3、合并集合(模板)
4、连通块中点的数量(模板)
5、格子游戏(《信息学奥赛一本通》)
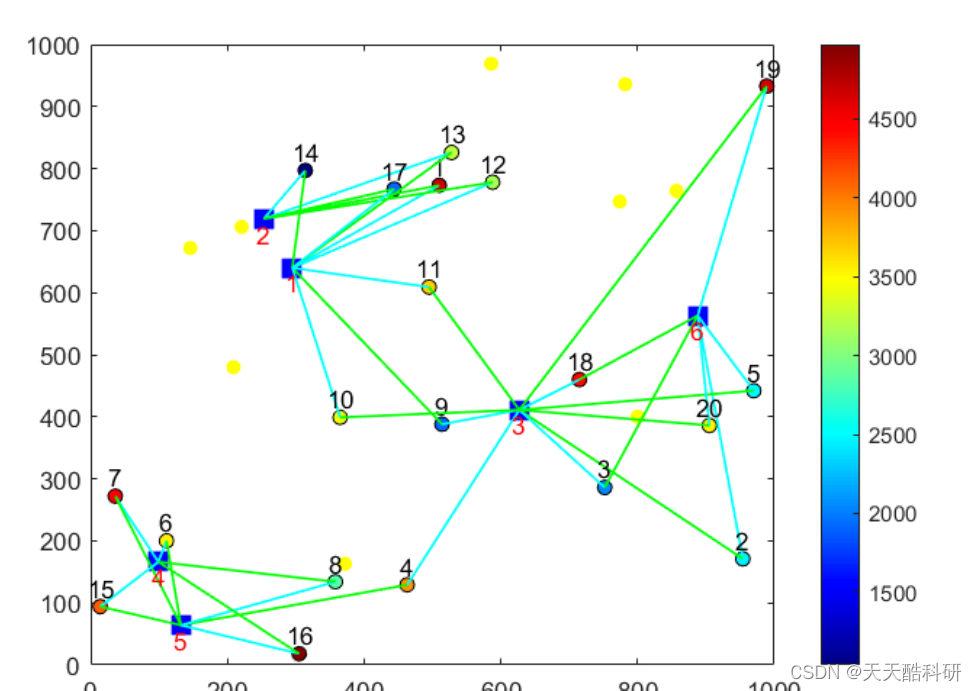
1、网络分析(第十一届蓝桥杯省赛第一场C++ A组/B组)
小明正在做一个网络实验。
他设置了 n 台电脑,称为节点,用于收发和存储数据。
初始时,所有节点都是独立的,不存在任何连接。
小明可以通过网线将两个节点连接起来,连接后两个节点就可以互相通信了。
两个节点如果存在网线连接,称为相邻。
小明有时会测试当时的网络,他会在某个节点发送一条信息,信息会发送到每个相邻的节点,之后这些节点又会转发到自己相邻的节点,直到所有直接或间接相邻的节点都收到了信息。
所有发送和接收的节点都会将信息存储下来。
一条信息只存储一次。
给出小明连接和测试的过程,请计算出每个节点存储信息的大小。
输入格式
输入的第一行包含两个整数 n,m,分别表示节点数量和操作数量。
节点从 1 至 n 编号。
接下来 m 行,每行三个整数,表示一个操作。
- 如果操作为
1 a b,表示将节点 a 和节点 b 通过网线连接起来。当 a = b 时,表示连接了一个自环,对网络没有实质影响。 - 如果操作为
2 p t,表示在节点 p 上发送一条大小为 t 的信息。
输出格式
输出一行,包含 n 个整数,相邻整数之间用一个空格分割,依次表示进行完上述操作后节点 1 至节点 n 上存储信息的大小。
数据范围
1≤n≤10000
1≤m≤1e5
1≤t≤100
输入样例1:
4 8
1 1 2
2 1 10
2 3 5
1 4 1
2 2 2
1 1 2
1 2 4
2 2 1
输出样例1:
13 13 5 3思路:
连接的时候创建一个新的根节点,作为祖先(通过创建新节点,可以实现在之后的dfs中不会将之前的信息加到后连接的计算机上)
依次执行输入的指令,传达的信息都加到根节点上
dfs,把发送的信息全部累加到根节点上
遍历输出根节点的信息(如果对于节点i,p[i]==i则说明这是个根节点,不然说明这个根节点已经其点的子节点了)
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=2e4+10,M=N<<1;
int p[N];
int h[M],e[M],ne[M],idx;
int add(int a,int b)
{
e[idx]=b;//值存到e里(idx是e的编号)
ne[idx]=h[a];//d的编号的下一个指向h【a】指向的编号
h[a]=idx++;//h【a】指向b的编号
}
int f[N];//存储信息
int n,m;
int find(int x)
{
if(x!=p[x])p[x]=find(p[x]);
return p[x];
}
void merge(int a,int b,int &root)
{
a=find(a);
b=find(b);
if(a!=b)
{
p[a]=p[b]=root;
add(root,a);
add(root,b);
root++;
}
}
void dfs(int son,int father)
{
f[son]+=f[father];
for(int i=h[son];i!=-1;i=ne[i])
{
int j=e[i];
dfs(j,son);
}
}
int main()
{
memset(h,-1,sizeof h);
cin>>n>>m;
for(int i=1;i<=n*2;i++)
{
p[i]=i;
}
int root=n+1;
while(m--)
{
int t,a,b;
cin>>t;
cin>>a>>b;
//cout<<"yes";
//cout<<m<<endl;
if(t==1)
{
merge(a,b,root);
}
else
{
a=find(a);
f[a]+=b;
}
//cout<<m<<endl;
}
//cout<<"yes1";
for(int i=n+1;i<root;i++)if(p[i]==i)dfs(i,0);//把每个根节点的值传递到每个计算机上
for(int i=1;i<=n;i++)cout<<f[i]<<" ";
return 0;
}
/*
4 8
1 1 2
2 1 10
2 3 5
1 4 1
2 2 2
1 1 2
1 2 4
2 2 1
13 13 5 3
*/2、奶酪(NOIP2017提高组)
现有一块大奶酪,它的高度为 h,它的长度和宽度我们可以认为是无限大的,奶酪中间有许多半径相同的球形空洞。
我们可以在这块奶酪中建立空间坐标系,在坐标系中,奶酪的下表面为 z=0,奶酪的上表面为 z=h。
现在,奶酪的下表面有一只小老鼠 Jerry,它知道奶酪中所有空洞的球心所在的坐标。
如果两个空洞相切或是相交,则 Jerry 可以从其中一个空洞跑到另一个空洞,特别地,如果一个空洞与下表面相切或是相交,Jerry 则可以从奶酪下表面跑进空洞;如果一个空洞与上表面相切或是相交,Jerry 则可以从空洞跑到奶酪上表面。
位于奶酪下表面的 Jerry 想知道,在不破坏奶酪的情况下,能否利用已有的空洞跑到奶酪的上表面去?
空间内两点 P1(x1,y1,z1)、P2(x2,y2,z2)的距离公式如下:
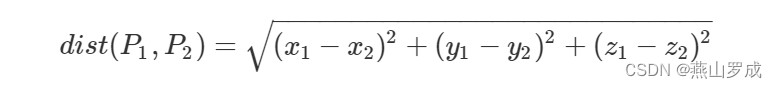
输入格式
每个输入文件包含多组数据。
输入文件的第一行,包含一个正整数 T,代表该输入文件中所含的数据组数。
接下来是 T组数据,每组数据的格式如下:
第一行包含三个正整数 n,h,和 r,两个数之间以一个空格分开,分别代表奶酪中空洞的数量,奶酪的高度和空洞的半径。
接下来的 n 行,每行包含三个整数 x、y、z,两个数之间以一个空格分开,表示空洞球心坐标为 (x,y,z)。
输出格式
输出文件包含 T 行,分别对应 T 组数据的答案,如果在第 i 组数据中,Jerry 能从下表面跑到上表面,则输出 Yes,如果不能,则输出 No。
数据范围
1≤n≤1000
1≤h,r≤1e9
T≤20
坐标的绝对值不超过1e9
输入样例:
3
2 4 1
0 0 1
0 0 3
2 5 1
0 0 1
0 0 4
2 5 2
0 0 2
2 0 4
输出样例:
Yes
No
Yes思路:
多源dfs(推荐)
或者并查集
代码:
多源bfs
#include <bits/stdc++.h>
using namespace std;
int t, n, h, r, f[1010];
double x[1010], y[1010], z[1010];
inline double dist(double X1, double X2, double Y1, double Y2, double Z1, double Z2) {
return sqrt((X1 - X2) * (X1 - X2) + (Y1 - Y2) * (Y1 - Y2) + (Z1 - Z2) * (Z1 - Z2));
}
int main() {
scanf("%d", &t);
while (t--) {
scanf("%d%d%d", &n, &h, &r);
for (int i = 1; i <= n; i++) scanf("%lf%lf%lf", &x[i], &y[i], &z[i]), f[i] = 0;
queue<int> q; bool ok = 0;
for (int i = 1; i <= n; i++)
if (z[i] <= r) q.push(i), f[i] = 1;
while (q.size()) {
int p = q.front(); q.pop();
if (ok) break;
if (z[p] + r >= h) {ok = 1; puts("Yes"); break;}
for (int i = 1; i <= n; i++) {
if (f[i]) continue;
if (dist(x[p], x[i], y[p], y[i], z[p], z[i]) <= 2 * r) {
q.push(i), f[i] = 1;
if (z[i] + r >= h) {ok = 1; puts("Yes"); break;}
}
}
}
if (!ok) puts("No");
}
return 0;
}
并查集:
#include <bits/stdc++.h>
using namespace std;
int t, n, h, r;
int t1, s1[1010], t2, s2[1010], fa[1010];
pair<long long, pair<long long, long long> > a[1010];
int get(int x) {
if (fa[x] != x) fa[x] = get(fa[x]);
return fa[x];
}
double dist(double X1, double X2, double Y1, double Y2, double Z1, double Z2) {
return sqrt(pow(X1 - X2, 2) + pow(Y1 - Y2, 2) + pow(Z1 - Z2, 2));
}
int main() {
scanf("%d", &t);
while (t--) {
scanf("%d%d%d", &n, &h, &r); t1 = 0, t2 = 0;
for (int i = 1; i <= n; i++) fa[i] = i;
for (int i = 1; i <= n; i++) {
scanf("%lld%lld%lld", &a[i].second.first, &a[i].second.second, &a[i].first);
if (a[i].first + r >= h) s1[++t1] = i;
if (a[i].first - r <= 0) s2[++t2] = i;
}
if (t1 == 0 || t2 == 0) {puts("No"); continue;}
for (int i = 1; i <= n; i++)
for (int j = i + 1; j <= n; j++) {
if (get(i) == get(j)) continue;
double d = dist(a[i].second.first, a[j].second.first, a[i].second.second, a[j].second.second, a[i].first, a[j].first);
if (d <= 2 * r) fa[get(i)] = get(j);
}
int b = 0;
for (int i = 1; i <= t1; i++) {
if (b) break;
for (int j = 1; j <= t2; j++)
if (get(s1[i]) == get(s2[j])) {puts("Yes"); b = 1; break;}
}
if (!b) puts("No");
}
return 0;
}3、合并集合(模板)
一共有 n 个数,编号是 1∼n,最开始每个数各自在一个集合中。
现在要进行 m 个操作,操作共有两种:
M a b,将编号为 a和 b的两个数所在的集合合并,如果两个数已经在同一个集合中,则忽略这个操作;Q a b,询问编号为 a 和 b 的两个数是否在同一个集合中;
输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为 M a b 或 Q a b 中的一种。
输出格式
对于每个询问指令 Q a b,都要输出一个结果,如果 a 和 b 在同一集合内,则输出 Yes,否则输出 No。
每个结果占一行。
数据范围
1≤n,m≤1e5
输入样例:
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4
输出样例:
Yes
No
Yes思路:
写好find函数和merge函数
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,m;
int p[N];
int find(int x)
{
if(x!=p[x])p[x]=find(p[x]);
return p[x];
}
void merge(int a,int b)
{
p[find(a)]=find(b);//a的祖先添加到b的祖先下面
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)p[i]=i;
while(m--)
{
char op;
int a,b;
cin>>op;
cin>>a>>b;
if(op=='M')
{
merge(a,b);
}
else
{
if(find(a)==find(b))cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
}
//Yes No
return 0;
} 4、连通块中点的数量(模板)
给定一个包含 n 个点(编号为 1∼n)的无向图,初始时图中没有边。
现在要进行 m 个操作,操作共有三种:
C a b,在点 a 和点 b之间连一条边,a 和 b 可能相等;Q1 a b,询问点 a 和点 b是否在同一个连通块中,a 和 b 可能相等;Q2 a,询问点 a 所在连通块中点的数量;
输入格式
第一行输入整数 n 和 m。
接下来 m 行,每行包含一个操作指令,指令为 C a b,Q1 a b 或 Q2 a 中的一种。
输出格式
对于每个询问指令 Q1 a b,如果 a和 b 在同一个连通块中,则输出 Yes,否则输出 No。
对于每个询问指令 Q2 a,输出一个整数表示点 a 所在连通块中点的数量
每个结果占一行。
数据范围
1≤n,m≤1e5
输入样例:
5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5
输出样例:
Yes
2
3
思路:
cnt数组统计连通块中点的数量(注意数量全放在祖先节点),合并函数(merge)中进行累加
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int n,m;
int p[N];
int cnt[N];
int find(int x)
{
if(x!=p[x])p[x]=find(p[x]);
return p[x];
}
void merge(int a,int b)
{
cnt[find(b)]+=cnt[find(a)];
p[find(a)]=find(b);
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
p[i]=i;
cnt[i]=1;
}
while(m--)
{
char op[5];
cin>>op;
if(op[0]=='C')
{
int a,b;
cin>>a>>b;
if(find(a)==find(b))continue;
merge(a,b);
}
else if(op[1]=='1')
{
int a,b;
cin>>a>>b;
if(find(a)==find(b))cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
else
{
int t;
cin>>t;
cout<<cnt[find(t)]<<endl;
}
}
return 0;
}5、格子游戏(《信息学奥赛一本通》)
Alice和Bob玩了一个古老的游戏:首先画一个 n×n的点阵(下图 n=3 )。
接着,他们两个轮流在相邻的点之间画上红边和蓝边:
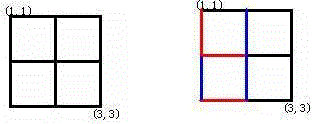
直到围成一个封闭的圈(面积不必为 1)为止,“封圈”的那个人就是赢家。因为棋盘实在是太大了,他们的游戏实在是太长了!
他们甚至在游戏中都不知道谁赢得了游戏。
于是请你写一个程序,帮助他们计算他们是否结束了游戏?
输入格式
输入数据第一行为两个整数 n 和 m。n表示点阵的大小,m 表示一共画了 m 条线。
以后 m 行,每行首先有两个数字 (x,y),代表了画线的起点坐标,接着用空格隔开一个字符,假如字符是 D,则是向下连一条边,如果是 R 就是向右连一条边。
输入数据不会有重复的边且保证正确。
输出格式
输出一行:在第几步的时候结束。
假如 m 步之后也没有结束,则输出一行“draw”。
数据范围
1≤n≤200
1≤m≤24000
输入样例:
3 5
1 1 D
1 1 R
1 2 D
2 1 R
2 2 D
输出样例:
4思路:
注意审题,"轮流在相邻的点之间画上红边和蓝边"表示不存在有孤立的线的情况
可以把每个点进行转换,变成一个独特的数,然后我们就可以把每个点存起来,如果新的两个点转化后,发现有共同祖先那就表示封圈了
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=4e4+9;//因为二维转化为一维了,所以一维空间必须开N的平方级 (200*200)
int p[N];
int find(int x)
{
if(x!=p[x])p[x]=find(p[x]);
return p[x];
}
void merge(int a,int b)
{
p[find(a)]=find(b);
}
int main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n*n;i++)p[i]=i;
int cnt=1;
for(int i=1;i<=m;i++)
{
int a,b;
char c;
cin>>a>>b>>c;
int p=(a-1)*n+b;//p表示原来的坐标
int q;//q表示另一端(向下或者向右)
if(c=='D')q=a*n+b;
else q=(a-1)*n+b+1;
//cout<<find(p)<<" "<<find(q)<<endl;
if(find(p)==find(q))
{
cout<<i;
return 0;
}
merge(p,q);
}
cout<<"draw";
return 0;
}