备战2024年蓝桥杯 -- 每日一题
Python大学A组
试题一:星空之夜
试题二:模拟散列表
试题三:字符串哈希
试题四:四数方和
试题五:扫雷
试题一:星空之夜
【题目描述】
夜空深处,闪亮的星星以星群的形式出现在人们眼中,形态万千。一个星群是指一组非空的在水平,垂直或对角线方向相邻的星星的集合。一个星群不能是一个更大星群的一部分。星群可能是相似的。如果两个星群的形状、包含星星的数目相同,那么无论它们的朝向如何,都认为它们是相似的。通常星群可能有 88 种朝向,如下图所示:
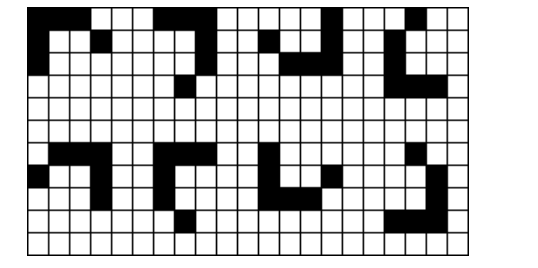
现在,我们用一个二维 0101 矩阵来表示夜空,如果一个位置上的数字是 11,那么说明这个位置上有一个星星,否则这个位置上的数字应该是 00。给定一个夜空二维矩阵,请你将其中的所有星群用小写字母进行标记,标记时相似星群用同一字母,不相似星群用不同字母。标注星群就是指将星群中所有的 11 替换为小写字母。
【输入格式】
第一行包含一个整数 W,表示矩阵宽度。
第二行包含一个整数 H,表示矩阵高度。
接下来 H 行,每行包含一个长度为 W 的 01序列,用来描述整个夜空矩阵。
【输出格式】
输出标记完所有星群后的二维矩阵。
用小写字母标记星群的方法很多,我们将整个输出读取为一个字符串,能够使得这个字符串字典序最小的标记方式,就是我们想要的标记方式。
输出这个标记方式标出的最终二维矩阵。
【输入格式】
0≤W,H≤100,
0≤星群数量 ≤500,
0≤0 不相似星群数量 ≤26,
1≤ 星群中星星的数量 ≤160
【输入样例】
23
15
10001000000000010000000
01111100011111000101101
01000000010001000111111
00000000010101000101111
00000111010001000000000
00001001011111000000000
10000001000000000000000
00101000000111110010000
00001000000100010011111
00000001110101010100010
00000100110100010000000
00010001110111110000000
00100001110000000100000
00001000100001000100101
00000001110001000111000【输出样例】
a000a0000000000b0000000
0aaaaa000ccccc000d0dd0d
0a0000000c000c000dddddd
000000000c0b0c000d0dddd
00000eee0c000c000000000
0000e00e0ccccc000000000
b000000e000000000000000
00b0f000000ccccc00a0000
0000f000000c000c00aaaaa
0000000ddd0c0b0c0a000a0
00000b00dd0c000c0000000
000g000ddd0ccccc0000000
00g0000ddd0000000e00000
0000b000d0000f000e00e0b
0000000ddd000f000eee000【解题思路】
哈希方式是每一个连通块中任意两个点的欧式距离累加。
【Python程序代码】
from collections import *
from math import *
w = int(input())
h = int(input())
st = []
hash,id,eps = [0]*30, int(0) ,0.000001
for i in range(h):
st.append(list(input()))
def dist(x1,y1,x2,y2):
return ((x1-x2)**2 + (y1-y2)**2)**0.5
def dfs(x,y):
q.append([x,y])
st[x][y]='0'
for i in range(x-1,x+2):
for j in range(y-1,y+2):
if i==x and j==y:continue
if i<0 or i>=h or j<0 or j>=w:continue
if st[i][j]=='1':
dfs(i,j)
def get_hash(q):
res = 0
for i in range(len(q)):
for j in range(i+1,len(q)):
res += dist(q[i][0],q[i][1],q[j][0],q[j][1])
return res
def get_id(res):
global id
for i in range(id):
if fabs(res-hash[i])<eps:
return chr( ord('a') + i )
hash[id] = res
id += 1
return chr(ord('a') + id -1)
for i in range(h):
for j in range(w):
if st[i][j]=='1':
q = []
dfs(i,j)
res = get_hash(q)
id1 = get_id(res)
for kx,ky in q:
st[kx][ky]=id1
for i in range(h):
for j in range(w):
print(st[i][j],end='')
print()
试题二:模拟散列表
【题目描述】
维护一个集合,支持如下几种操作:
I x,插入一个整数 x;Q x,询问整数 x 是否在集合中出现过;
现在要进行 N次操作,对于每个询问操作输出对应的结果。
【输入格式】
第一行包含整数 N,表示操作数量。
接下来 N 行,每行包含一个操作指令,操作指令为 I x,Q x 中的一种。
【输出格式】
对于每个询问指令 Q x,输出一个询问结果,如果 x 在集合中出现过,则输出 Yes,否则输出 No。
每个结果占一行。
【数据范围】
1≤N≤105
−109≤x≤109
【输入样例】
5
I 1
I 2
I 3
Q 2
Q 5【输出样例】
Yes
No【解题思路】
用set+in
【Python程序代码】
n = int(input())
s = set()
for i in range(n):
a,b = map(str,input().split())
if a=='I':
s.add(b)
else:
if b in s:print('Yes')
else:print('No')试题三:字符串哈希
【题目描述】
给定一个长度为 n 的字符串,再给定 m 个询问,每个询问包含四个整数 l1,r1,l2,r2,请你判断 [l1,r1]和 [l2,r2] 这两个区间所包含的字符串子串是否完全相同。字符串中只包含大小写英文字母和数字。
【输入格式】
第一行包含整数 n 和 m,表示字符串长度和询问次数。
第二行包含一个长度为 n 的字符串,字符串中只包含大小写英文字母和数字。
接下来 m 行,每行包含四个整数 l1,r1,l2,r2,表示一次询问所涉及的两个区间。
注意,字符串的位置从 11 开始编号。
【输出格式】
对于每个询问输出一个结果,如果两个字符串子串完全相同则输出 Yes,否则输出 No。
每个结果占一行。
【数据范围】
1≤n,m≤105
【输入样例】
8 3
aabbaabb
1 3 5 7
1 3 6 8
1 2 1 2【输出样例】
Yes
No
Yes【解题思路】
模板提
【Python程序代码】
n,m = map(int,input().split())
s = " " + input()
mod = 1<<64
N,P = 1000010,131
h,p = [0]*N,[0]*N
def get_hash(l,r):
return (h[r] - h[l-1]*p[r-l+1] + mod)%mod
p[0]=1
for i in range(1,n+1):
p[i] = (p[i-1]*P)%mod
h[i] = (h[i-1]*P + ord(s[i]))%mod
for _ in range(m):
l1,r1,l2,r2 = map(int,input().split())
if get_hash(l1,r1)==get_hash(l2,r2):print('Yes')
else:print('No')试题四:四数平方和
【题目描述】
四平方和定理,又称为拉格朗日定理:每个正整数都可以表示为至多 4 个正整数的平方和。如果把 0 包括进去,就正好可以表示为 4 个数的平方和。比如:
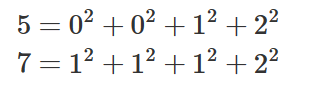
对于一个给定的正整数,可能存在多种平方和的表示法。要求你对 44 个数排序:
0≤a≤b≤c≤d
并对所有的可能表示法按 a,b,c,d 为联合主键升序排列,最后输出第一个表示法。
【输入格式】
输入一个正整数 N。
【输出格式】
输出4个非负整数,按从小到大排序,中间用空格分开。
【数据范围】
0<N<5∗106
【输入样例】
5
【输出样例】
0 0 1 2
【解题思路】
先枚举两个数的平方和,然后再枚举两个。
【Python程序代码】
n = int(input())
h = [-1]*(n*5)
for c in range(0,int(n**0.5)+2):
for d in range(c,int(n**0.5)+2):
if h[c*c+d*d]!=-1:continue
else:h[c*c+d*d] = c
def work():
for a in range(0,int(n**0.5)+1):
for b in range(a,int((n/2)**0.5)+1):
t = n - a*a -b*b
if h[t]==-1:continue
else:
d = int((t - h[t]**2)**0.5)
print(a,b,h[t],d)
return
work()