论文地址:link
代码:link
摘要
我们提出了卷积块注意力模块(CBAM),这是一种简单而有效的用于前馈卷积神经网络的注意力模块。给定一个中间特征图,我们的模块依次推断沿着两个独立维度的注意力图,通道和空间,然后将这些注意力图与输入特征图相乘,进行自适应特征细化。由于CBAM是一个轻量级和通用的模块,它可以无缝地集成到任何CNN架构中,几乎没有额外开销,并且可以与基础CNN一起端到端地进行训练。我们通过在ImageNet-1K、MS COCO检测和VOC 2007检测数据集上进行大量实验来验证我们的CBAM。 我们的实验证明,在各种模型中,分类和检测性能均有一致的提升,展示了CBAM的广泛适用性。
1.介绍
卷积神经网络(CNN)凭借其丰富的表示能力,显著提升了视觉任务的性能[1,2,3]。为了增强CNN的性能,最近的研究主要探讨了网络的三个重要因素:深度、宽度和基数。。除了这些因素,我们研究了架构设计的另一个方面,即注意力。注意力的重要性在前的文献中得到了广泛研究[12,13,14,15,16,17]。注意力不仅告诉我们要关注哪里,还改善了感兴趣的表示。我们的目标是通过使用注意力机制增强表示能力:专注于重要特征并抑制不必要的特征。在本文中,我们提出了一个新的网络模块,名为“卷积块注意力模块”。由于卷积操作通过将跨通道和空间信息混合在一起提取信息特征,我们采用我们的模块来强调这两个主要维度上的有意义特征:通道和空间轴。为了实现这一点,我们依次应用通道和空间注意力模块(如图1所示),以便每个分支可以分别学习在通道和空间轴上关注“什么”和“哪里”。
主要贡献
1.我们提出了一个简单而有效的注意力模块(CBAM),可以广泛应用于提升CNN的表示能力。
2.我们通过广泛的消融研究验证了我们的注意力模块的有效性。
3.我们验证了在多个基准测试(ImageNet-1K、MS COCO和VOC 2007)上,通过插入我们的轻量级模块,各种网络的性能得到了显著提升。
2.卷积块注意模块
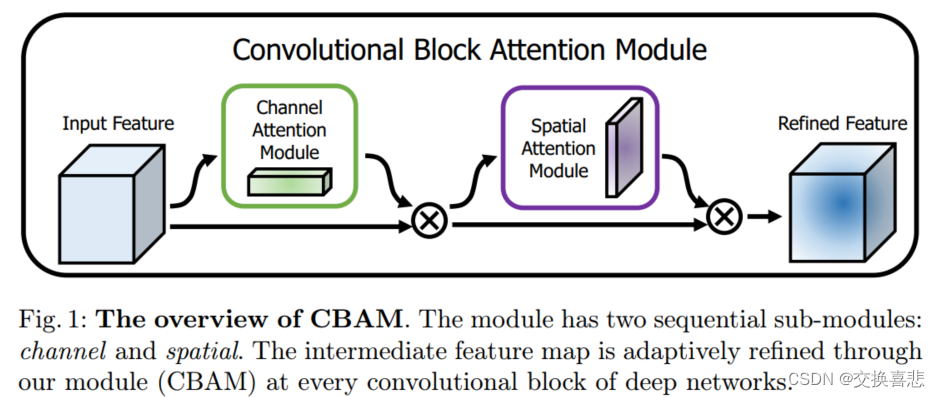
给定一个中间特征图
F
∈
R
C
×
H
×
W
F \in {R^{C \times H \times W}}
F∈RC×H×W作为输入,CBAM 依次推断出一个1D通道注意力图
M
c
∈
R
C
×
1
×
1
{M_c} \in {R^{C \times 1 \times 1}}
Mc∈RC×1×1和一个 2D 空间注意力图
M
s
∈
R
1
×
H
×
W
{M_s} \in {R^{1 \times H \times W}}
Ms∈R1×H×W,如图1所示。总体注意力过程可以总结为:
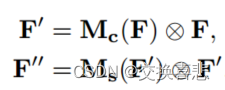
在这里,符号 ⊗ 表示逐元素乘法。在乘法过程中,注意力值相应地进行广播(复制):通道注意力值沿空间维度广播,反之亦然。F ′′ 是最终的精炼输出。图2描述了每个注意力图的计算过程。以下描述了每个注意力模块的细节。
2.1 Channel attention module
利用特征的通道间关系来生成通道注意力图,特征图的每个通道都被视为特征检测器,通道注意力集中在给定输入图像的情况下“什么”是有意义的,为了有效地计算通道注意力,压缩输入特征图的空间维度,使用平均池化和最大池化特征。利用这两个特征可以极大地提高网络的表示能力,而不是单独使用每个特征。
首先利用平均池化和最大池化操作来聚合特征图的空间信息,生成两个不同的空间上下文描述符,
F
a
v
g
c
F_{avg}^c
Favgc和
F
m
a
x
c
F_{max}^c
Fmaxc,分别表示平均池化特征和最大池化特征。然后,这两个描述符都被转发到共享网络以生成我们的通道注意力图
M
c
∈
R
C
×
1
×
1
{M_c} \in {R^{C \times 1 \times 1}}
Mc∈RC×1×1 。共享网络由具有一个隐藏层的多层感知器(MLP)组成。为了减少参数开销,隐藏激活大小设置为
R
C
/
r
×
1
×
1
R ^{C/r×1×1}
RC/r×1×1 ,其中 r 是缩减比率。将共享网络应用于每个描述符后,我们使用逐元素求和来合并输出特征向量。简而言之,通道注意力计算如下:
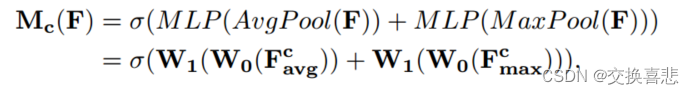
其中 σ 表示 sigmoid 函数,W0 ∈
R
C
/
r
×
C
R^{C/r×C}
RC/r×C ,W1 ∈
R
C
×
C
/
r
R^{C×C/r}
RC×C/r 。请注意,两个输入共享 MLP 权重
W
0
W_0
W0和
W
1
W_1
W1,并且 ReLU 激活函数后面跟着
W
0
W_0
W0。
2.2 Spatial attention module
利用特征的空间关系生成空间注意力图。与通道注意力不同,空间注意力关注的是“哪里”,这是信息性的部分,与通道注意力是互补的。为了计算空间注意力,我们首先沿着通道轴应用平均池化和最大池化操作并将它们连接起来以生成有效的特征描述符。沿着通道轴应用池化操作被证明可以有效地突出显示信息区域。在级联特征描述符上,我们应用卷积层来生成空间注意力图
M
s
(
F
)
∈
R
H
×
W
{M_s}\left( F \right) \in {R^{H \times W}}
Ms(F)∈RH×W,它对强调或抑制的位置进行编码。下面我们描述详细操作。通过使用两个池化操作来聚合特征图的通道信息,生成两个2D图:
F
a
v
g
s
∈
R
1
×
H
×
W
F_{avg}^s \in {R^{1 \times H \times W}}
Favgs∈R1×H×W 和
F
m
a
x
s
∈
R
1
×
H
×
W
F_{max}^s \in {R^{1 \times H \times W}}
Fmaxs∈R1×H×W。每个表示整个通道的平均池化特征和最大池化特征。然后,它们通过标准卷积层连接和卷积,生成我们的 2D 空间注意力图。简而言之,空间注意力计算如下:
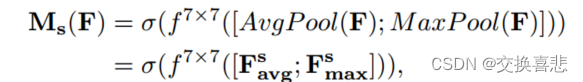
其中σ表示sigmoid函数,f 7×7表示滤波器尺寸为7×7的卷积运算。
注意力模块的安排。给定输入图像,两个注意力模块(通道和空间)计算互补注意力,分别关注“什么”和“哪里”。考虑到这一点,两个模块可以并行或顺序放置。我们发现顺序排列比并行排列提供更好的结果。对于顺序过程的安排,我们的实验结果表明,通道优先顺序略好于空间优先顺序。
代码实现:
import torch
import math
import torch.nn as nn
import torch.nn.functional as F
class BasicConv(nn.Module):
def __init__(self, in_planes, out_planes, kernel_size, stride=1, padding=0, dilation=1, groups=1, relu=True, bn=True, bias=False):
super(BasicConv, self).__init__()
self.out_channels = out_planes
self.conv = nn.Conv2d(in_planes, out_planes, kernel_size=kernel_size, stride=stride, padding=padding, dilation=dilation, groups=groups, bias=bias)
self.bn = nn.BatchNorm2d(out_planes,eps=1e-5, momentum=0.01, affine=True) if bn else None
self.relu = nn.ReLU() if relu else None
def forward(self, x):
x = self.conv(x)
if self.bn is not None:
x = self.bn(x)
if self.relu is not None:
x = self.relu(x)
return x
class Flatten(nn.Module):
def forward(self, x):
return x.view(x.size(0), -1)
class ChannelGate(nn.Module):
def __init__(self, gate_channels, reduction_ratio=16, pool_types=['avg', 'max']):
super(ChannelGate, self).__init__()
self.gate_channels = gate_channels
self.mlp = nn.Sequential(
Flatten(),
nn.Linear(gate_channels, gate_channels // reduction_ratio),
nn.ReLU(),
nn.Linear(gate_channels // reduction_ratio, gate_channels)
)
self.pool_types = pool_types
def forward(self, x):
channel_att_sum = None
for pool_type in self.pool_types:
if pool_type=='avg':
avg_pool = F.avg_pool2d( x, (x.size(2), x.size(3)), stride=(x.size(2), x.size(3)))
channel_att_raw = self.mlp( avg_pool )
elif pool_type=='max':
max_pool = F.max_pool2d( x, (x.size(2), x.size(3)), stride=(x.size(2), x.size(3)))
channel_att_raw = self.mlp( max_pool )
elif pool_type=='lp':
lp_pool = F.lp_pool2d( x, 2, (x.size(2), x.size(3)), stride=(x.size(2), x.size(3)))
channel_att_raw = self.mlp( lp_pool )
elif pool_type=='lse':
# LSE pool only
lse_pool = logsumexp_2d(x)
channel_att_raw = self.mlp( lse_pool )
if channel_att_sum is None:
channel_att_sum = channel_att_raw
else:
channel_att_sum = channel_att_sum + channel_att_raw
scale = F.sigmoid( channel_att_sum ).unsqueeze(2).unsqueeze(3).expand_as(x)
return x * scale
def logsumexp_2d(tensor):
tensor_flatten = tensor.view(tensor.size(0), tensor.size(1), -1)
s, _ = torch.max(tensor_flatten, dim=2, keepdim=True)
outputs = s + (tensor_flatten - s).exp().sum(dim=2, keepdim=True).log()
return outputs
class ChannelPool(nn.Module):
def forward(self, x):
return torch.cat( (torch.max(x,1)[0].unsqueeze(1), torch.mean(x,1).unsqueeze(1)), dim=1 )
class SpatialGate(nn.Module):
def __init__(self):
super(SpatialGate, self).__init__()
kernel_size = 7
self.compress = ChannelPool()
self.spatial = BasicConv(2, 1, kernel_size, stride=1, padding=(kernel_size-1) // 2, relu=False)
def forward(self, x):
x_compress = self.compress(x)
x_out = self.spatial(x_compress)
scale = F.sigmoid(x_out) # broadcasting
return x * scale
class CBAM(nn.Module):
def __init__(self, gate_channels, reduction_ratio=16, pool_types=['avg', 'max'], no_spatial=False):
super(CBAM, self).__init__()
self.ChannelGate = ChannelGate(gate_channels, reduction_ratio, pool_types)
self.no_spatial=no_spatial
if not no_spatial:
self.SpatialGate = SpatialGate()
def forward(self, x):
x_out = self.ChannelGate(x)
if not self.no_spatial:
x_out = self.SpatialGate(x_out)
return x_out