深度学习Top10算法之深度神经网络DNN

深度神经网络（Deep Neural Networks，DNN）是人工神经网络（Artificial Neural Networks，ANN）的一种扩展。它们通过模仿人脑的工作原理来处理数据和创建模式，广泛应用于图像识别、语音识别、自然语言处理等领域。

一、背景

早期发展（1940s-1980s）

1940年代初期：神经网络的最初概念源于Warren McCulloch和Walter Pitts的工作。他们提出了一种简化的大脑神经元模型，并展示了其计算潜力。
1958年：Frank Rosenblatt发明了感知机（Perceptron），这是一种二进制输出的简单神经网络，可执行简单的分类任务。
1969年：Marvin Minsky和Seymour Papert出版了《Perceptrons》，指出了感知机的局限性，尤其是它不能解决线性不可分问题（如异或问题）。这导致了第一次AI冬天。

BP算法（1980s）

1980年代初期：多层神经网络和反向传播算法（Backpropagation，BP）的发展标志着神经网络研究的复兴。特别是，1986年，David Rumelhart、Geoffrey Hinton和Ronald Williams发表了一篇关键论文，详细描述了BP算法。这种算法能够有效地训练多层网络，并解决了感知机面临的某些限制。

深度学习的崛起（2000s-2010s）

2006年：Geoffrey Hinton和他的学生在一篇论文中重新引入了深度神经网络的概念，提出了一种新的无监督预训练方法。这标志着深度学习时代的开始。
2012年：Alex Krizhevsky、Ilya Sutskever和Geoffrey Hinton发布了AlexNet的论文。这个模型在ImageNet竞赛中大获全胜，展示了深度学习在视觉识别任务中的巨大潜力。
随后几年：深度学习在各个领域迅速崛起，特别是在计算机视觉、自然语言处理等领域。诸如卷积神经网络（CNN）、循环神经网络（RNN）以及长短期记忆网络（LSTM）等架构的发展，进一步推动了这一领域的发展。

二、原理介绍

深度神经网络的原理

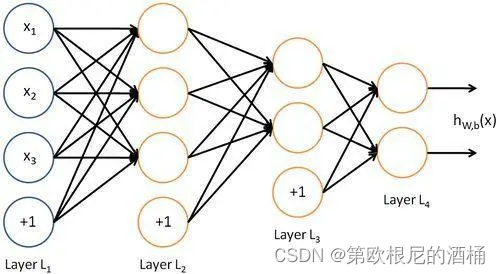
深度神经网络（DNN）的基本构成包括输入层、若干隐藏层和输出层。每个层由多个神经元（或称为节点）组成，这些神经元通过带权重的连接相互作用。下面是DNN的基本数学原理和公式：

1. 神经元模型

每个神经元接收来自前一层神经元的输入，计算加权和，并应用一个激活函数。一个神经元的输出可以表示为：

$f\left(\sum_{i=1}^{n} w_i x_i + b\right)$

其中：

$x_i$ 是输入值，
$w_i$ 是对应的权重，
$b$ 是偏置项，
$f$ 是激活函数（如ReLU、Sigmoid等）。

2. 前向传播

在前向传播过程中，数据从输入层经过每一隐藏层直到输出层。每一层的输出都是下一层的输入。

3. 激活函数

激活函数是用来引入非线性因素的，使得网络能够学习和执行更复杂的任务。常用的激活函数包括：

ReLU： $\max(0, x)$
Sigmoid： $\frac{1}{1 + e^{-x}}$
Tanh： $\tanh(x)$

4. 损失函数

损失函数（Loss Function）用于评估模型的预测值与真实值之间的差距。常见的损失函数包括均方误差（MSE）用于回归任务，交叉熵（Cross-Entropy）用于分类任务。

5. 反向传播与梯度下降

反向传播算法用于计算每个权重对于总损失的影响。基于这个影响，通过梯度下降算法更新权重，以减小损失函数的值。权重更新公式为：

$\eta \cdot \frac{\partial L}{\partial w}$

其中：

$w$ 是权重，
$\eta$ 是学习率，
$\frac{\partial L}{\partial w}$ 是损失函数相对于权重的梯度。

6. 优化器

优化器是用来更新网络的权重以减小损失函数值的算法。常见的优化器包括随机梯度下降（SGD）、Adam等。

通过这些步骤，DNN能够从数据中学习复杂的模式和关系，适用于广泛的预测和分类任务。
在这里插入图片描述

三、项目具体案例：基于DNN的衣服分类

数据集

我们将使用著名的Fashion MNIST数据集，它包含了70000张灰度图像，分为10个类别，每个类别有7000张图像。图像的尺寸为28x28像素。

实现步骤

1.导入所需库：首先导入TensorFlow和其他必要的Python库。
2.加载和预处理数据：加载Fashion MNIST数据集，并进行适当的预处理。
3.定义模型：构建一个深度神经网络模型。
4.编译模型：定义损失函数、优化器和评估指标。
5.训练模型：使用训练数据训练模型。
6.评估模型：使用测试数据评估模型的性能。
7.模型预测：对新图像进行预测分类。

示例代码

以下是用于上述任务的Python代码示例。请注意，这是一个简化的示例，实际应用可能需要更详细的调参和优化。

import tensorflow as tf
from tensorflow.keras.datasets import fashion_mnist
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Flatten
from tensorflow.keras.optimizers import Adam

# 加载数据集
(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()

# 数据预处理
train_images = train_images / 255.0
test_images = test_images / 255.0

# 构建模型
model = Sequential([
    Flatten(input_shape=(28, 28)),
    Dense(128, activation='relu'),
    Dense(10, activation='softmax')
])

# 编译模型
model.compile(optimizer=Adam(),
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

# 训练模型
model.fit(train_images, train_labels, epochs=10)

# 评估模型
test_loss, test_acc = model.evaluate(test_images, test_labels)
print('Test accuracy:', test_acc)

# 使用模型进行预测
predictions = model.predict(test_images)

这段代码首先导入了必要的库，然后加载Fashion MNIST数据集，并对其进行简单的归一化处理。之后，我们构建了一个简单的神经网络模型，包括一个输入层（通过Flatten层实现），两个Dense层作为隐藏层和输出层。接着，我们编译并训练了模型，并在测试集上评估了其性能。最后，我们使用训练好的模型对新图像进行预测。

四、优势与不足

深度神经网络（DNN）是当今人工智能和机器学习领域中最为突出的技术之一，其应用广泛，影响深远。然而，正如任何技术一样，DNN在拥有显著优势的同时，也存在一些不可忽视的不足。以下是对深度神经网络优势与不足的详细分析：

DNN的优势

强大的数据表示能力
DNN通过学习大量数据中的复杂模式，能够自动提取和构建有效的数据表示。与传统的机器学习方法相比，DNN不需要人工设计特征，而是可以从原始数据中直接学习到深层次的特征表示。
多层次的特征学习
在DNN中，每个隐藏层都可以看作是在进行一种特征的转换和抽象。较低层可能学习到数据的基本元素（如边缘或颜色），而更高层则能够识别更复杂的模式（如物体或人脸）。这种分层学习使得DNN在处理复杂问题时更加高效。
灵活性和通用性
DNN的架构设计非常灵活，可以通过改变层数、神经元数目、激活函数等来调整网络结构，从而适应不同类型的数据和任务，如图像识别、语音识别和自然语言处理等。
大数据驱动
随着大数据时代的到来，DNN能够利用其强大的数据处理能力，在海量数据中进行学习，这使得其性能随着数据量的增加而提高。
不断的技术进步
DNN领域不断有新的研究和技术进展，比如各种新型神经网络架构（如卷积神经网络CNN、循环神经网络RNN）和优化算法，这些进步持续推动着DNN在各个领域的应用。

DNN的不足

对数据和计算资源的高需求
DNN通常需要大量的训练数据来实现有效的学习，这在某些情况下可能难以满足。此外，DNN的训练和推理过程计算量大，对硬件资源（如GPU）的需求高。
过拟合的风险
在数据量有限或者模型过于复杂的情况下，DNN容易发生过拟合，即模型在训练数据上表现良好，但在新数据上性能下降。
可解释性问题
DNN的决策过程往往被视为一个“黑盒”，其内部是如何处理数据和做出决策的，往往缺乏直观的解释。这在需要决策透明度的应用中，如医疗诊断，成为一个重要问题。
长期依赖问题
在某些类型的DNN（尤其是RNN）中，模型可能难以学习输入序列中的长期依赖关系。虽然有如LSTM这样的结构来解决这个问题，但它们仍然有其局限性。
对噪声和对抗样本的脆弱性
DNN在面对包含噪声的数据或者特意设计的对抗样本时，其性能的稳定性和鲁棒性可能会显著降低。这种脆弱性在安全敏感的应用中尤为重要，如自动驾驶汽车和欺诈检测系统。
调参难度大
虽然DNN提供了极大的灵活性，但这也意味着需要调整大量的超参数，如学习率、层数、神经元数量等。合适的参数选择对于模型的性能至关重要，而找到最优参数组合往往需要大量的实验和经验。
非平稳和动态环境下的挑战
DNN通常在静态数据集上训练得到最佳性能。然而，在实际应用中，数据可能是非平稳的（即数据分布随时间变化），这需要模型具有动态适应能力，而传统DNN在这方面可能存在不足。
训练和调试的复杂性
DNN的训练过程可能非常复杂和时间消耗巨大。此外，当模型表现不佳时，确定问题所在并不总是直观的，这可能导致调试过程费时费力。
能源效率
DNN的训练和推理过程通常需要大量计算资源，这导致较高的能源消耗。在可持续性和环境影响日益受到重视的背景下，这一点成为一个重要考量。
泛化能力的限制
虽然DNN在训练集上的表现可能很好，但它们在面对与训练数据显著不同的新数据时，泛化能力可能有限。这表明DNN可能在学习数据分布的特定方面，而不是获取到真正通用的知识。