Abstract
寻找使网络影响力最大化的种子集是一个众所周知的 NP 难题。尽管贪心算法可以提供接近最优的解决方案,但影响估计的子问题导致解决方案效率低下。在这项工作中,我们提出了 GLIE,这是一种图神经网络,它学习如何估计独立级联的影响扩散。 GLIE 依赖于通过监督训练收紧的理论上限。实验表明,它可以为比训练集大 10 倍的真实图提供准确的影响估计。随后,我们将其纳入两种影响力最大化技术中。我们首先利用成本有效的惰性前向优化,用 GLIE 代替蒙特卡罗模拟,尽管存在计算开销,但超越了基准。为了提高计算效率,我们基于 GLIE 的表示开发了一种可证明的子模块影响力传播,在自适应构建种子集的同时对节点进行排名。所提出的算法是归纳性的,这意味着它们在少于 300 个节点和最多 5 个种子的图上进行训练,并在具有数百万个节点和最多 200 个种子的图上进行测试。最终方法展示了最有希望的时间效率和影响质量的组合,优于几个基线。
关键词:影响力最大化、图神经网络、图表示学习
I. INTRODUCTION
几个现实世界的问题可以转化为图上的组合优化问题。从分发包裹 [1] 到车辆管理 [2],图上的优化是许多对我们生活方式至关重要的现实问题的核心。不幸的是,这些问题大多数都是 NP 困难的,因此我们只能在符合现实世界要求的令人满意的时间限制内近似解决它们。最近的机器学习方法已成为开发提供快速且准确的近似值的启发式方法的有前途的解决方案。总体思路是训练监督或无监督学习模型,以在给定不可见的图和问题约束的情况下推断解决方案。这些模型往往由用于对图和节点进行编码的图神经网络 (GNN)、用于生成顺序预测的 Qlearning [3] 或两者的组合组成。学习解决组合优化问题背后的实际动机是推理时间比运行精确组合求解器更快[4]。据说,专门的组合算法,如解决旅行商问题 (TSP) 的 CONCORDE 或一般的 GUROBI,目前还无法被超越 [5]。
尽管已经针对大量问题提出了许多此类方法,但影响最大化(IM)尚未得到广泛解决。 IM 解决了在网络中找到一组节点的问题,该组节点可以通过开始扩散来最大化到达的节点数量 [6]。该问题被证明是NP-hard问题,从约简到集合覆盖问题。此外,IM 中嵌入的影响估计 (IE) 问题,即估计受给定种子集影响的节点数量,是#P-困难的,需要 2|E|精确计算的可能组合,其中 |E|是网络边的数量[7]。通常,影响估计是使用独立级联 (IC) 扩散模型的重复蒙特卡罗 (MC) 模拟来近似的[8]。一般来说,种子集是贪婪地构建的,利用影响函数的子模性,保证至少 (1 − 1 e ) 逼近最优值。尽管后者缺乏效率,因为在构建种子集的每一步中仍然必须估计每个候选种子的影响。因此,利用草图或图的结构开发了几种可扩展算法 [9]、[10] 和启发式算法 [11],以产生更有效的解决方案。
我们使用图神经网络来解决 IM,以利用上述优势及其轻松合并用户配置文件和主题等上下文信息的能力 [12],这是非专业 IM 算法和启发式方法仍然无法解决的任务。我们提出了 GLIE,这是一种 GNN,它为给定的种子集提供高效的 IE 和具有影响概率的图。它可以用作独立的影响预测器,对于比训练集大 10 倍的图表,具有具有竞争力的结果。此外,我们利用 GLIE 进行 IM,并将其与 CELF [13] 相结合,这通常不会扩展到具有数千个边的网络之外。所提出的方法可以在数秒内运行在具有数百万条边的网络中,并且比最先进的算法和之前的 IM 的 GNN-RL 方法表现出更好的影响力传播。此外,我们提出了 PUN,一种使用 GLIE 的表示来计算预测不受影响的邻居数量的方法,并将其用作边际增益的近似值。我们证明 PUN 的影响力传播是次模且单调的,因此可以在有保证的情况下进行贪婪优化,相比之下,到先前基于学习的方法。实验表明,PUN 在影响力质量和效率之间提供了最佳平衡。
本文的结构如下。第二节概述了相关方法并阐明了所提出模型的优点。第三节描述了所提出的方法,从 IE 开始,逐步发展到更快的 IM 方法。第四节介绍了 IE 和 IM 的实验结果。最后,第五节总结了贡献并提出了未来的步骤。
II. RELATED WORK
使用神经网络解决组合优化 (CO) 的第一种方法是基于离散结构的注意力神经网络 POINTERNETS [14],然后是一种将 POINTERNETS 与 actor-critic 训练相结合的架构,以找到 TSP 的最佳路径 [15] 。第一个利用基于图的学习的架构是 S2N-DQN [16],它使用 STRUCT2VEC 对节点和图的状态进行编码,并训练一个深度 Q 网络 (DQN) 模型,该模型选择正确的节点添加到给定当前状态的解决方案。
基于S2V-DQN,最近提出了一种用于网络拆除问题的DQN[17]。该模型名为 FINDER,采用深度 Q 学习架构,其中表示由三个 GRAPHSAGE 层导出。奖励基于巨型连接组件的大小,即选择的每个新节点(种子)的目标是尽可能地拆除网络。 FINDER 的一些主要优点是它是在小型合成数据上进行训练的,这些数据很容易制作,并且可以外推到相对较大的图表。另一方面,核心缺点之一是它不能与有向图和加权边一起工作。最近 IM 上的另一种监督深度学习方法 GCOMB [18],利用概率贪婪在图上生成分数并训练 GNN 来预测它们。 Q 网络接收分数以及节点与种子集的邻域相关性的近似计算,以预测下一个种子。这种方法虽然具有可扩展性并且在准确度上与 SOTA 相当,但必须在图的大型随机子集(其中 30%)上进行训练,并在其余部分上进行测试。这使得模型图特定,即必须重新训练才能在新图上表现良好。考虑到使用传统 IE 的概率贪婪方法训练、二次采样和标记这些样本所需的时间,这会带来严重的开销。如 [18] 附录 G 所示,它需要数百分钟以上的时间,因此超出了我们的范围。另一个解决影响力预测的 GNN 是[19]。 DEEPIS使用影响概率矩阵的幂序列和两层GNN来回归每个节点的敏感性。随后,估计根据 IC 概率在邻居中传播。 DEEPIS 是一种与 GLIE 不同的架构,GLIE 仅接收种子集的指示。此外,DEEPIS 在影响最大化方面没有经过广泛的测试,正如我们将在实验部分看到的,它对影响概率矩阵幂的使用不利于其可扩展性。最后,最近一项关于学习一般性近似的工作子模块策略 [20] 需要一个特定的模型来捕获 IM 的状态,这设计起来并不简单。基于学习的 IM 的一个不同分支依赖于扩散级联 [21] 等补充信息来导出更有效的 IM 算法 [22]。这显然与当前的方法相反,当前的方法没有从典型的 IM 设置中假设任何进一步的信息。
在本文中,我们提出了一种结合上述方法优点的方法,即仅在小型模拟数据上进行一次训练并推广到更大的图,并解决了加权有向网络中的 IM 问题。此外,该方法可以分为用于影响力估计的 GNN 和两种 IM 方法。前者可以单独作为影响预测器,并与相关方法竞争,例如用于比训练集大一倍的图的 DMP [23]。 GLIE用于提出:(1)CELF-GLIE,C ELF [13],以GLIE作为影响估计器; (2) PUN,一种自适应 IM 方法 [24],它使用 GLIE 的表示贪婪地优化子模影响扩散。
我们在这里注意到,大多数关于组合优化深度学习的相关文献都涉及小图[14]、[16],这使得它们不适用于我们的任务。更具可扩展性的无监督方法 [25] 是针对特定问题量身定制的,并且对于调整我们的问题来说并非易事,但 [26] 除外,它被发现比我们与 [18] 相比的 SOTA 算法要差得多。
III. METHODOLOGY
A. GLIE: Graph Learning-based Influence Estimation
在本节中,我们介绍 GLIE,这是一种 GNN 模型,旨在学习如何估计种子集 S 对图 G = (V, E) 的影响。设 A ∈ Rn×n 为邻接矩阵,X ∈ Rn×d 为节点的特征,否则用 1 和 0 表示哪些节点属于种子集:
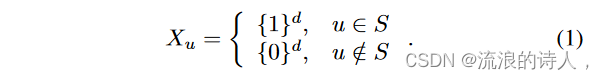
对于接下来的分析,我们设置 d = 1。当我们对问题进行参数化时,更多维度将变得有意义。如果我们按每一行对 A 进行归一化,我们将形成一个行随机转移矩阵,如下所示:
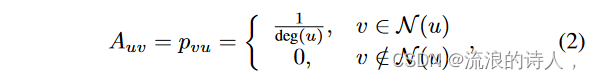
其中 deg(u) 是节点 u 的入度,N (u) 是 u 的邻居集合。基于加权级联模型 [6],每一行 u 存储节点 u 受到通过有向链路 v → u 连接到它的每个其他节点影响的概率。请注意,在有向影响图的情况下,A 应对应于邻接矩阵的转置。影响概率 p(u|S) 类似于节点 u 的邻居在种子集中(即在扩散的第一步期间)受到影响的概率。我们可以用消息传递来计算 u 的 p(u|S) 的众所周知的上限 ˆ p(u|S):

其中第二个等式源于加权级联的定义和[27],App. 中的证明的不等式。 A. 由于扩散覆盖超过一跳,推导需要重复乘法以近似总影响扩散。具体来说,计算与种子集不相邻的节点的影响概率需要递归地估计其邻居受种子影响的概率。如果我们让 H1 = A·X,并且假设新的种子集 St 是步骤 t − 1 中受影响的节点,则它们的概率存储在 Ht 中,就像离散时间中的扩散一样。然后我们可以用 Ht+1 = A·Ht 重新计算新的影响概率。
定理 1. 重复乘积 Ht+1 = A · Ht 计算步骤 t + 1 时每个受感染节点的实际影响概率的上限。

在 (6) 中,根据 IC 的定义,我们有 p(u|v) = pvpvu,因此 p(u|S) = 1 − Q v∈N (u)∩S (1 − pvpvu),其中 pv = 1对于 v ∈ S1,它们是确定性激活的初始种子集。因此,(6)成立,并且这些概率是真实影响概率的上限。因此,影响力分布 ˆ σ(S) = P (u,v)εE puv 是实际 σ(S) 的上限。
实际上,由于循环的存在,会出现两个问题。首先,如果重复这个过程,原始种子的影响力可能会再次增加,这与独立级联模型相反。这可以通过最小化重复来控制,例如,四次重复导致原始种子能够用三角形重新感染网络中的其他节点。为此,我们利用多达三个神经网络层。循环引起的另一个问题与邻居相互影响的概率有关。在这种情况下,方程中互补概率的乘积。 (4) 不对非独立邻居进行因式分解。这种效应在[23],App. 中进行了广泛的分析。 B,并证明由 p(u|S) 计算的影响概率本身就是有环图的真实影响概率的上限。直观上,代表非独立概率的乘积大于独立概率的乘积。这使得与产品互补的真实影响概率小于我们计算的值。
因此,我们可以认为估计 ^ p(u|S) 提供了真实影响概率的上限,并且我们可以使用它来计算给定种子集的真实影响力传播的上限,即种子集的总数受扩散影响的节点。由于消息传递本质上可以计算影响力估计的近似值,因此我们可以将其参数化以学习一个基于监督加强该近似值的函数。在我们的神经网络架构中,每一层都由一个 GNN 组成,这里省略了批量归一化和 dropout,从 H0 = X ∈ Rn×d 开始,我们有:
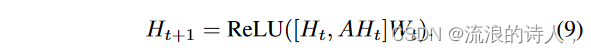
基于所有节点表示总结图形表示的读出函数是具有跳过连接的求和:
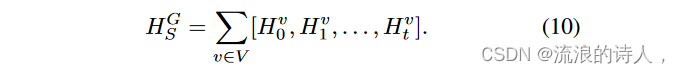
该表示捕获了每层中所有节点处于活动状态的概率。表示预测影响力传播的输出由以下公式得出:
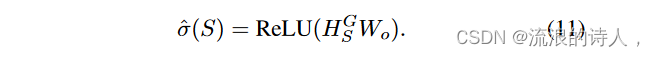
我们的损失函数是一个简单的最小二乘回归。请注意,在 Wt 是 [0, 1] 中未经训练的正半定高斯随机矩阵的情况下,每层 Hv t 的表示将对应于种子集 t 跳邻居影响概率的上限 [23] 。一旦权重 Wt 被训练,这个上限就不会保留。在我们的方法中,中间层 Wt 的参数经过训练,使得上限减小,并且最终层 Wo 可以结合概率来导出受影响节点总数的累积估计。我们通过检查图 1 中所示的层激活来实证验证这一点。热图表明预期受到影响的列(节点)之间存在差异,这意味着我们不仅可以预测数量,还可以预测谁将受到影响。然而,由于 ^ σ 是由多层导出的,因此关系确定确切受影响集的阈值并不简单。
B. CELF-GLIE: Cost Effective Lazy Forward with GLIE
成本有效的惰性前向(CELF)[13]是影响力最大化的贪婪算法的改进版本,它利用子模块性的特性来有效地选择种子节点。通过根据影响力分布维护节点的排序列表,CELF 识别出每次迭代中边际增益最高的最佳节点,与贪婪算法相比,执行时间明显加快,同时又不牺牲其原始有效性。在我们的例子中,我们提出了一种调整,用 GLIE 的输出替换基于 MC IC 的原始 CELF IE。由于我们没有证明 ^ σ 的子模性,因此我们不能认为保留了理论保证,因此我们将其用作启发式。 CELFGLIE 有两个主要的计算瓶颈。首先,第一步需要计算每个节点的初始IE。其次,虽然它减轻了在每一步中测试每个节点的需要,但它仍然需要在每一步中至少一个节点使用 IE。第二,我们将努力缓解这两个问题。
C. PUN: Potentially Uninfluenced Neighbors
第一步计算每个节点的影响力分布对计算量要求很高。因此,我们寻求一种能够克服这一障碍并提供足够性能的方法。我们首先利用上面提到的激活来定义与该层相对应的步骤上受影响的节点集。设 ˆ LS, L′S ∈ {0, 1}n 分别为预测不受影响节点和预测受影响节点中值为 1 的二元向量:
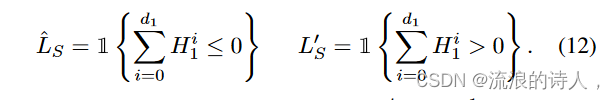
其中 T 是层数,Hi t ∈ Rn×1 是 Ht 中的一列。该向量包含每个节点的标签,其符号指示预测该节点是否会受到影响。 L′S 提供一个粗略的估计,但它允许更简单的影响范围,我们可以贪婪地优化:
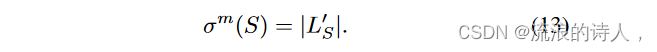
我们可以使用 ^ LS 和消息传递来预测节点不受影响的邻域数量,即潜在不受影响的邻居(PUN),由节点 u 各自的影响概率加权,
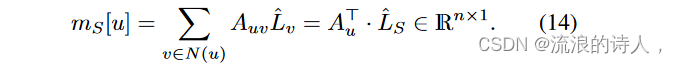
为了提高效率,我们可以计算 mS = A⊤ ˆ L,它可以被认为是所有节点对其直接邻居的边际增益的近似值。因此,我们可以使用 arg max(mS) 对其进行优化,如图 (1) 所示。为了证明 σm 可以在 (1 − 1 e )OPT 的理论保证下进行贪婪优化,在定理 2 中我们证明了它的单调性和子模性。
定理 2. 影响扩散 σm 是次模且单调的。
证明。证明可以在附录 A 中找到。
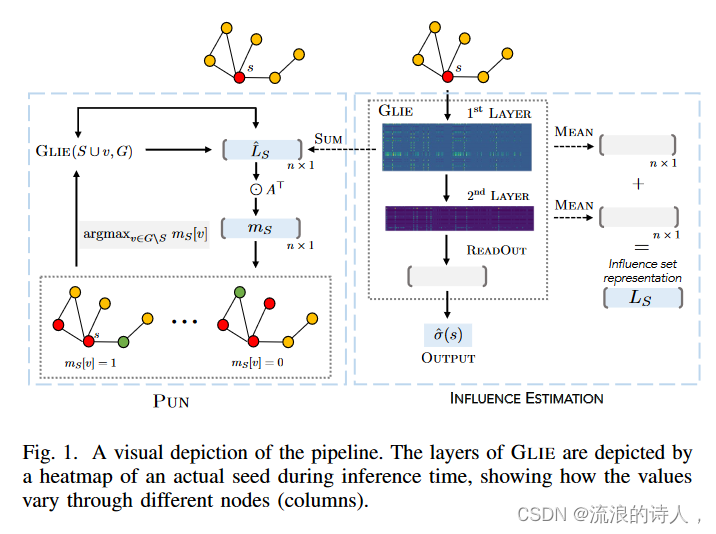
图 1. 管道的直观描述。 GLIE 的各层由推理时间内实际种子的热图描绘,显示不同节点(列)的值如何变化。
PUN 可以在图 1 的左侧看到。我们首先将第一个种子设置为具有最高度数的节点,这可以被认为是一个安全的假设,因为在实践中它始终是种子集的一部分。我们使用 GLIE(S, G) 来检索 ^ LS,我们用它来根据 arg maxv∈G\S mS[v] 和新的 ^ LS∪{v} 查找下一个节点。 PUN 的一个缺点是 σm 低估了预测的影响。与上限 DMP 相比,σm 不如 ^ σ 准确,但允许我们有效地计算边际增益的子模代理。这种低估意味着网络中被认为在 LS 中不受影响的部分被测量为其邻居的潜在增益,因此基于 mS 的排名可能会受到负面影响。为此,我们将使用自适应全反馈选择(AFF),在选择新的种子节点后,我们将其与预测受影响的节点一起从网络中删除。 [28]的开创性工作已经证明,子模单调函数的 AFF 贪心算法保证与最优策略具有竞争性的性能。在我们的例子中,我们将每 k 个种子使用一次 AFF 更新,因为如果我们在每一步中都这样做,它会增加少量的计算开销。 PUN 的好处是双重的。首先,当我们删除受影响的节点并截断种子集时,GLIE 会产生越来越有效的估计,因为当图和种子集较小时,它的性能会更好。其次,随着邻域大小的减小,遗漏受影响节点的影响以毫秒为单位减小。
IV. EXPERIMENTAL EVALUATION
所有实验均在配备 NVIDIA GPU TITAN V(12GB RAM)、256GB RAM 和 Intel(R) Xeon(R) W-2145 CPU @ 3.70GHz 的 PC 上进行。源代码可以在补充文件中找到。
A. Influence Estimation
为了训练影响力估计任务,我们创建了一组标记样本,每个样本由种子集 S 和相应的影响力分布 σ(S) 组成。我们创建了 100 个 Barabasi-Albert [29] 和 Holme-Kim [30] 无向图,范围从 100 到 200 个节点,以及 30 个从 300 到 500 个节点。 60% 用于训练,20% 用于验证,20% 用于测试。我们使用这些网络模型是因为度分布类似于现实世界的网络。影响概率是根据加权级联模型分配的,即节点 u 受其 N (u) 个节点影响的概率相等 1/deg(u)。该模型需要有向图,因此我们通过附加反向边将所有无向图转换为有向图。尽管估计影响概率本身就是一个问题[31],但在没有额外数据的情况下,加权级联被认为比纯随机分配更现实[6]。为了标记样本,我们使用 1, 000 个蒙特卡罗 (MC) IC 运行 CELF 算法进行影响估计,最多可处理 5 个种子。请注意,我们预计运行 10, 000 次模拟将提供更定性的监督。然而,一方面,训练时间会呈指数级增长,另一方面,由于训练图相对较小,差异很小。存储大小 1 至 5 的最佳种子集,以及每个种子集大小的 30 个随机负样本。这总共有 20、150 个训练样本。 GLIE 的每个训练样本对应于图 G、种子集 S 和用作回归标签的真实影响范围 σ(S) 的三元组。随机种子集用于捕获大约该大小的种子集预期的平均影响力传播。这会创建“平均样本”,它将构成其他问题中的整个数据集。然而,在 IM 中,平均种子集和最优种子集之间的 σ 差异可能很大,因此仅对随机集进行训练将使我们的模型无法预测与最优值相对应的较大值。这就是为什么我们添加了上述使用 CELF 计算的最佳种子集样本的原因。我们认为 30 个随机和 1 个最优的组合是一种更平衡的监督形式,因为您期望绝大多数种子集具有平均 σ。
关于模型训练,我们使用验证集使用小规模网格搜索来找到最佳批量大小 64、dropout 0.4、层数 2、隐藏层大小 64 和特征维度 50。更重要的是,我们观察到它是随着深度的增加,有利于减小隐藏层大小(2 倍),即从 32 到 16。这意味着 1 跳节点表示比 2 跳节点表示更有用,依此类推 - 验证上述结论是方程中影响估计的近似值。 (4)随着消息传递深度的增加,分歧更大。然后训练进行 100 个 epoch,提前停止 50 个,学习率为 0.01。
我们用三种不同类型的图表来评估模型。第一个是上面提到的数据集的测试集。第二个是一组 10 个幂律大图 (1, 000 – 2, 000节点)来评估模型在大一倍的网络中泛化的能力。第三个是一组三个现实世界图,即犯罪 (CR)、HI-II-14 (HI) 和 GR 协作 (GR)
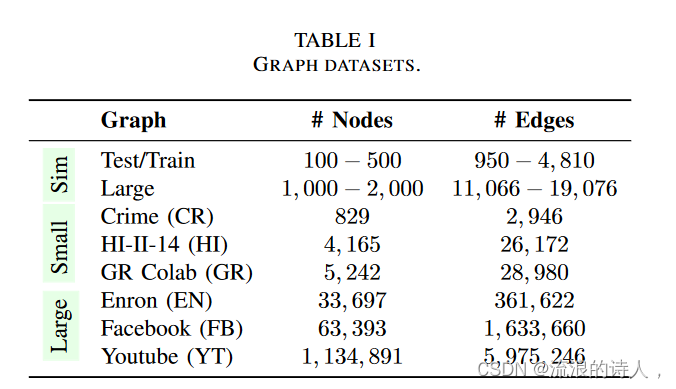
表 I 中给出了有关数据集的更多信息。
针对不同的种子集大小(从 2 到 10)评估真实图表,以测试我们的模型推断更大种子集大小的能力。由于后两个图(HI 和 GR)的大小,我们对每个种子集大小采用基于度的顶部节点作为最佳种子集,以及用于大型模拟图的 30 个随机种子集和用于模拟图的 3 个随机种子集。真实图,以验证模型在不重要的节点集中的准确性。我们将影响力估计的准确性与 DMP [23] 进行了比较。我们无法利用 UBLF [27] 的影响力估计,因为加权级联模型违反了其中心条件,并且计算出的影响力被夸大到超过了网络节点。
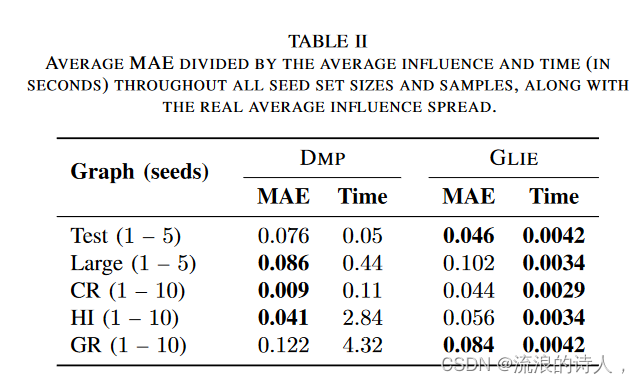
平均 MAE 除以所有种子集大小和样本的平均影响力和时间(以秒为单位),以及实际平均影响力传播。
所有数据集的平均误差和平均影响以及平均时间如表二所示。
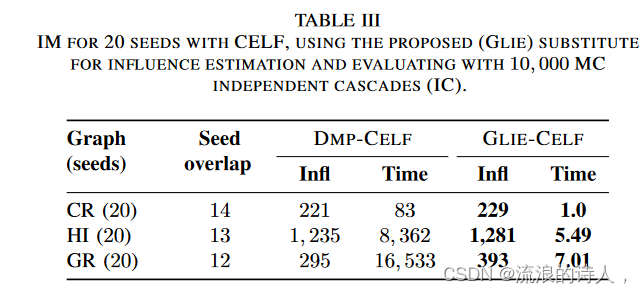
使用 CELF 对 20 个种子进行 IM,使用建议的 (GLIE) 替代品进行影响估计并使用 10, 000 MC 独立级联 (IC) 进行评估。
我们使用独立级联评估检索到的种子集,结果如表III所示。我们应该在此强调,使用具有 1, 000 MC IC 的传统方法,此任务对于犯罪数据集需要超过 3 个小时,而对于 GR 则需要几天的时间。正如我们在表 III 中看到的,GLIECELF 可以显着加速计算时间,同时检索的种子更加有效。此外,在 CELF 中,大部分时间消耗在影响力分布的初始计算上,即计算 100 个种子而不是表 III 中所示的 20 个种子的开销,对于三个数据集分别为 0.11、0.22 和 0.19 秒。
B. Influence Maximization
我们的主要基准是最先进的 IM 方法 IMM [10],它利用反向可达集 [9] 来估计影响力。具体来说,它会生成一系列此类草图,并使用它们来近似影响范围,而无需进行模拟。这在理论上保证了显着的加速。请注意,IMM 被认为是最先进的算法之一,并且超越了各种启发式算法 [32]。我们按照作者的建议设置 e = 0.5。我们还与 FINDER 进行了比较,后者在第二节中进行了分析,并与独立的最著名的启发式方法进行了比较。
级联。 PMIA [7] 根据局部近似计算影响范围。 DEGREEDISCOUNT [11]使用节点的度构建种子集,该种子集根据当前种子集及其影响力重新计算。最后,K-CORES [33] 是一个图简并度量,它揭示了属于密集连接子图的节点
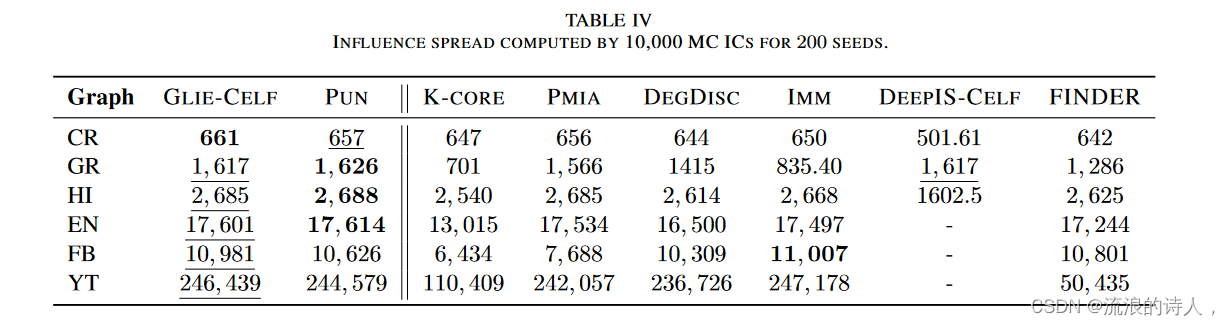 通过 MC IC 模拟计算得出的 200 个种子的影响力传播结果如表 IV 所示,
通过 MC IC 模拟计算得出的 200 个种子的影响力传播结果如表 IV 所示,
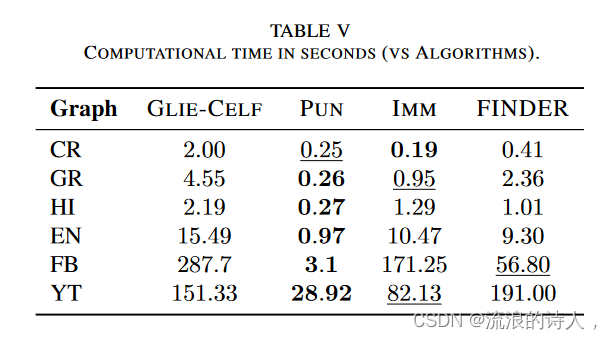

而时间结果如表 V 和表 VI 所示。最好的结果以粗体显示,次好的结果以下划线显示。可以看出,与其他方法相比,GLIECELF 总体上表现出优越的影响质量,但速度相当慢。 PUN 在每一步中只需要一次影响估计,并且不需要初始计算。与 IMM 相比,它的加速速度是 IMM 的 3 到 60 倍,而从较小的图移动到较大的图的计算开销与节点数量呈次线性关系。就影响力质量而言,PUN 在大多数数据集中排名第一或第二,并且随着种子集大小的增加,这种影响变得更加明显。 DEGDISC 在较小的图中比 PUN 更快,但在较大的图中较慢,而且种子集质量总体较差。 PMIA 提供中等种子集质量,但计算效率低下。 IMM 显然不是最快的方法,但它非常准确,特别是对于较小的种子组尺寸。 FINDER 表现出最不准确的性能,这是可以理解的,因为它解决了相关问题,而不完全是 IC 的 IM。给出的计算时间是解决节点渗透所需的时间,在这种情况下,它可能检索比 100 个节点更大的种子集。因此,我们可以假设对于有限的种子集来说,它的速度相当快,但检索到的种子的质量是所有方法中最不准确的。总的来说,我们可以认为 PUN 提供了最好的准确率-效率所检查方法的权衡。
正如相关工作中分析的那样,DEEPIS 与 GLIE 类似,因为它使用神经网络计算影响力估计。我们遵循作者的方法,并使用他们在提议的 Cora ML [19] 上的代码来训练模型。我们将其用作 CELF 中的影响力估计预言机,类似于 GLIE-CELF。不幸的是,由于需要影响矩阵的显式幂(需要超过 24 GB 的 GPU RAM),因此无法扩展到更大的数据集。为了进行比较,该模型对于 CR、GR 和 HI 数据集分别需要 501.61、835.4 和 1、602.5 秒。这进一步证明了PUN的优越性。
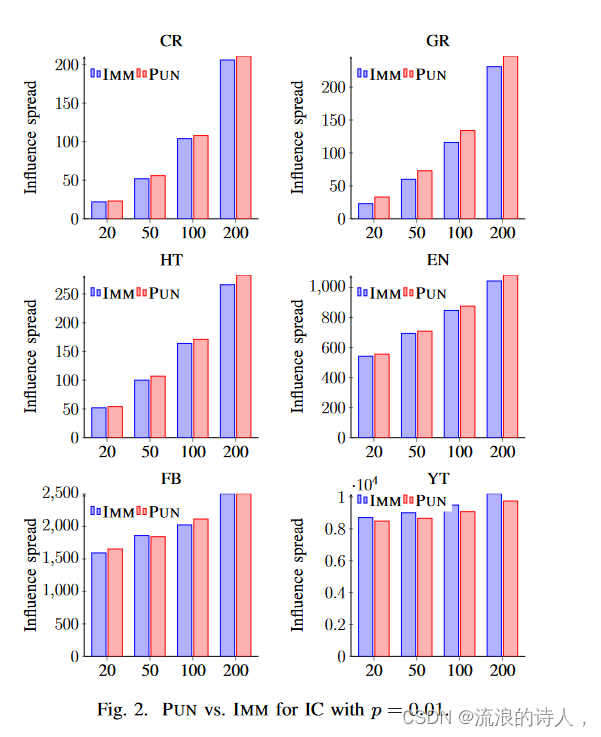
此外,我们在图 2 中的相同影响概率 p = 0.01 的相同图上比较 IMM 和 PUN,作为加权级联分配的替代。我们观察到 PUN 的表现优于 IMM。最后,我们进行了一个实验,在不使用 GPU 的情况下对 100 个种子进行 PUN 比较。
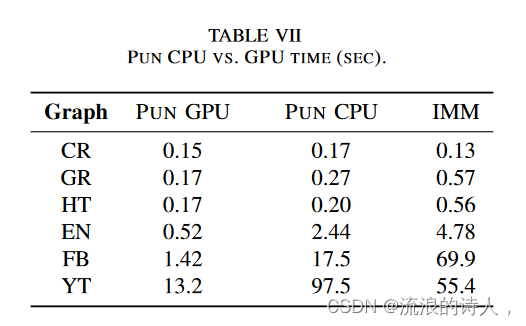
结果报告于表VII中。可以看出,GPU 提供了显着的加速,但即使没有 GPU,PUN 仍然是更快的选择。
V. CONCLUSION
我们提出了 GLIE,一种基于 GNN 的影响力估计模型。我们展示了它在该任务中的准确性,并进一步利用它来解决 IM 问题。我们基于 GLIE.G LIE-CELF 的表示和预测开发了两种方法,GLIE.G LIE-CELF 是一种经典算法的改进,超越了 SOTA,但计算开销很大,而 textscPun 是一个子模块函数,充当边际增益,并且可以自适应优化,在效率和精度之间取得平衡。
对于典型的 IM 算法来说,考虑共享信息的主题或用户的特征并不简单[34]。神经网络方法的一个显着的实际优势是通过在输入中添加相应的嵌入来轻松合并此类补充数据,就像在类似设置中所做的那样[12]。因此,如果有适当的数据集,我们认为使用上下文信息进行实验是自然的下一步。最后,我们还计划研究训练强化学习模块的潜力,即从扩散的每个步骤接收真实的反馈,从而更新 Q-NET 和 GLIE。这将允许模型根据扩散过程中收到的部分反馈来调整其决策。