一 、 递归套路解决判断完全二叉树
1.1 描述
1.2 分析
1.2 分析
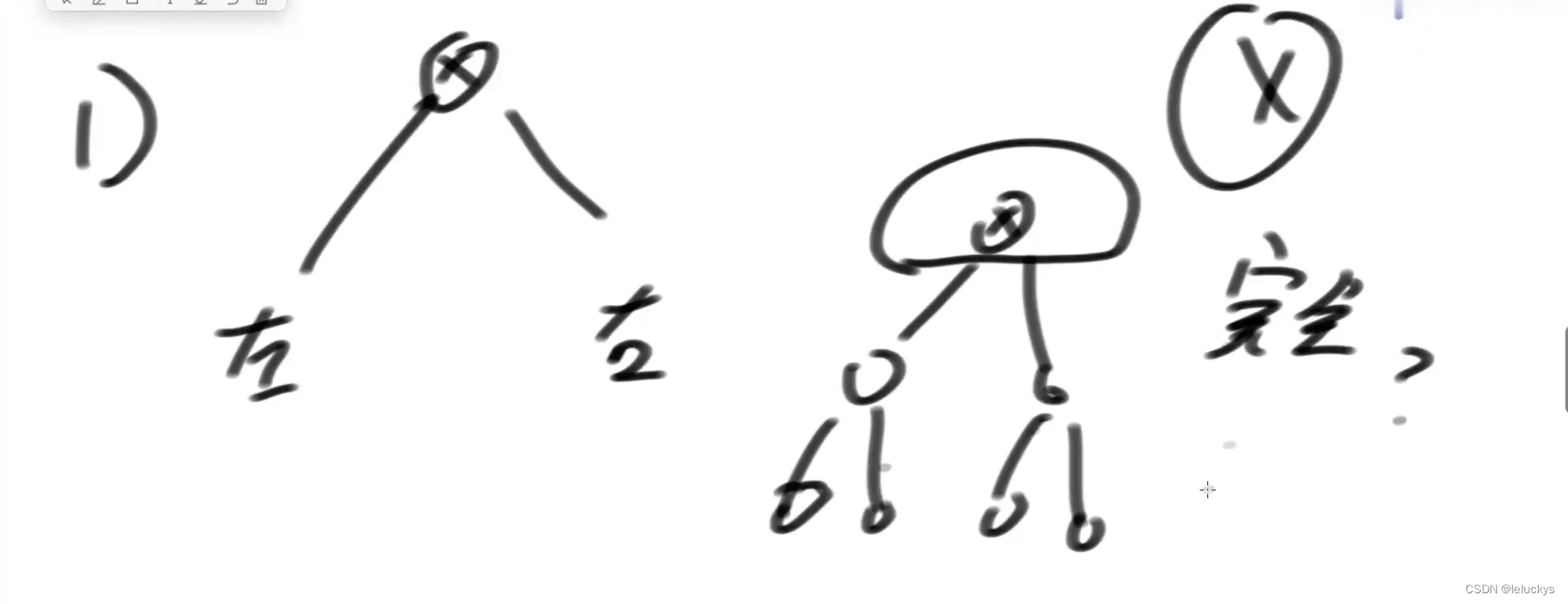
第二种
第三种
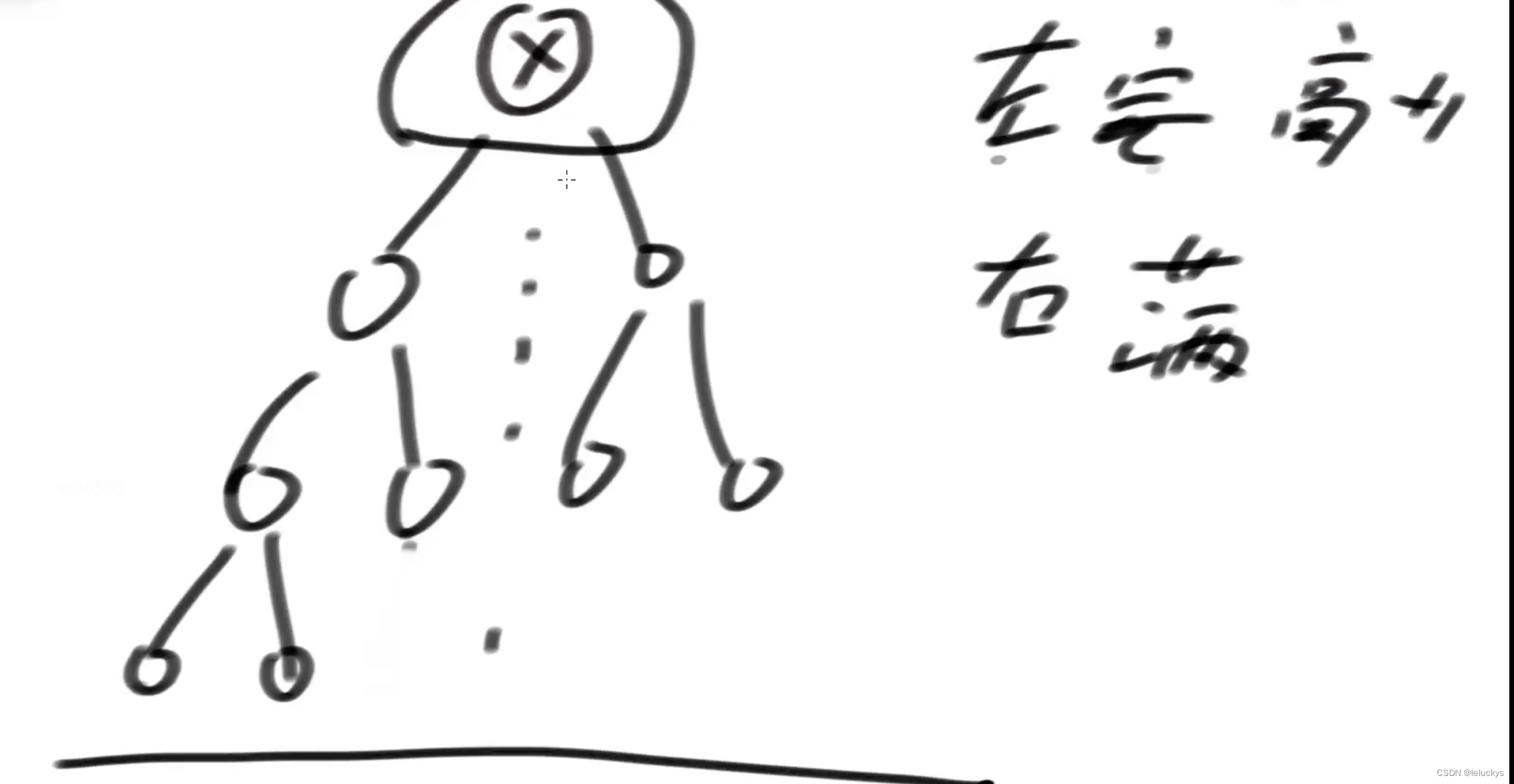
第四种

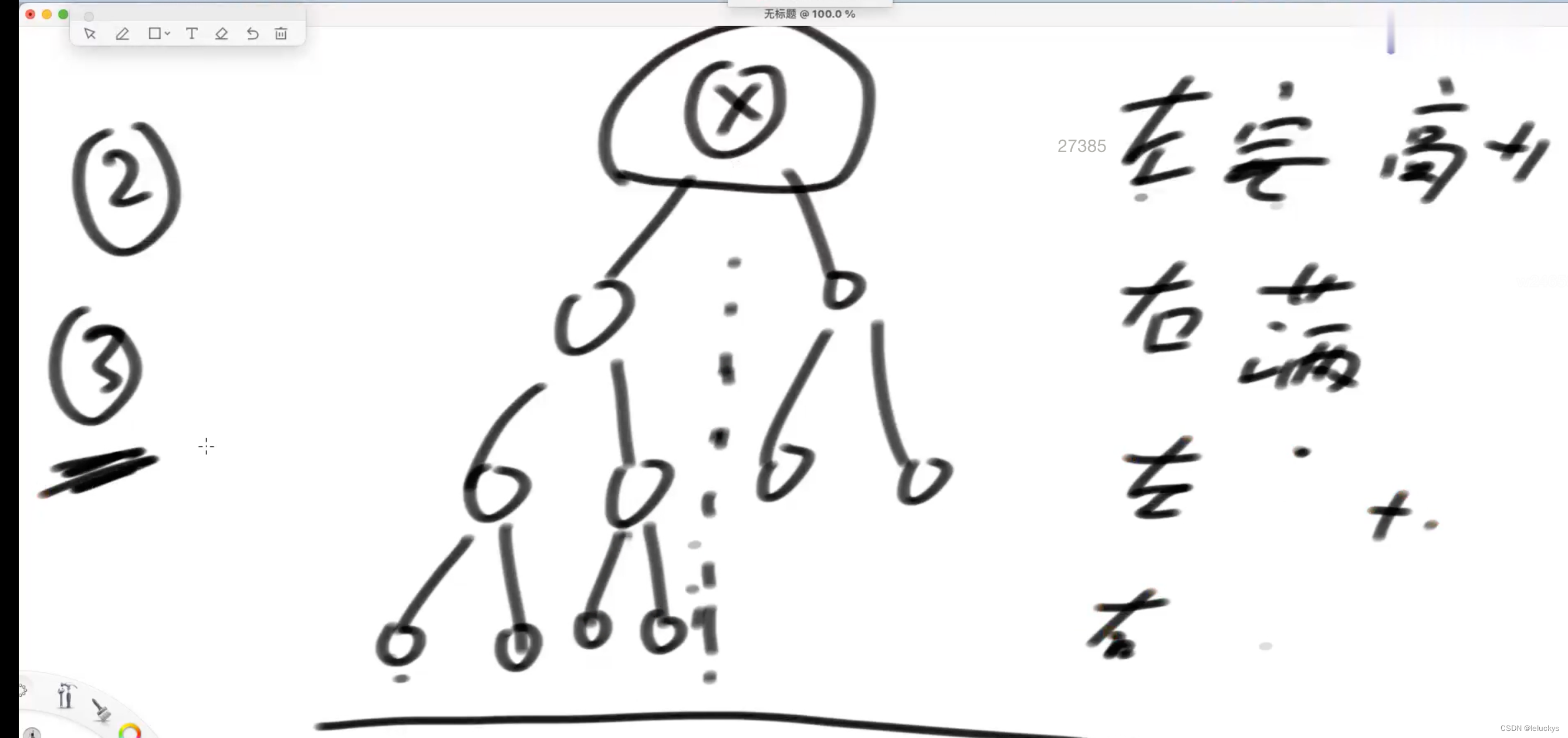
1.3 代码
public static boolean isCBT2(Node head) {
return process(head).isCBT;
}
public static class Info {
public boolean isFull;
public boolean isCBT;
public int height;
public Info(boolean full, boolean cbt, int h) {
isFull = full;
isCBT = cbt;
height = h;
}
}
public static Info process(Node x) {
if (x == null) {
return new Info(true, true, 0);
}
Info leftInfo = process(x.left);
Info rightInfo = process(x.right);
int height = Math.max(leftInfo.height, rightInfo.height) + 1;
boolean isFull = leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height;
boolean isCBT = false;
if (leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height) {
isCBT = true;
} else if (leftInfo.isCBT && rightInfo.isFull && leftInfo.height == rightInfo.height + 1) {
isCBT = true;
} else if (leftInfo.isFull && rightInfo.isFull && leftInfo.height == rightInfo.height + 1) {
isCBT = true;
} else if (leftInfo.isFull && rightInfo.isCBT && leftInfo.height == rightInfo.height) {
isCBT = true;
}
return new Info(isFull, isCBT, height);
}
二 最大的二叉搜索子树的头节点
2.1 描述
给定一棵二叉树的头节点head,
返回这颗二叉树中最大的二叉搜索子树的头节点
2.2 分析
2.3 代码
三 返回a和b的最低公共祖先
2.1 描述
2.2 分析
2.2.1 使用 hashset
在遍历二叉树的时候,可以将每个节点的父节点存到map里面,比如说要找a,b的最低公共祖先,先遍历a的所有父节点放到set里面,再遍历b看b的节点是否在set里面就能找到了
public class Code03_lowestAncestor {
public static class Node {
public int value;
public Node left;
public Node right;
public Node(int data) {
this.value = data;
}
}
public static Node lowestAncestor1(Node head, Node o1, Node o2) {
if (head == null) {
return null;
}
HashMap<Node, Node> parentMap = new HashMap<>();
parentMap.put(head, null);//head节点的父节点是null
fillParentMap(head, parentMap);
HashSet<Node> o1Set = new HashSet<>();
Node cur = o1;
o1Set.add(cur);
while (parentMap.get(cur) != null) {
cur = parentMap.get(cur);
o1Set.add(cur);
}
cur = o2;
while (!o1Set.contains(cur)) {
cur = parentMap.get(cur);
}
return cur;
}
public static void fillParentMap(Node head, HashMap<Node, Node> parentMap) {
if (head.left != null) {
parentMap.put(head.left, head);
fillParentMap(head.left, parentMap);
}
if (head.right != null) {
parentMap.put(head.right, head);
fillParentMap(head.right, parentMap);
}
}
}
2.2.2 递归套路解决该问题

 2.3 代码
2.3 代码
public static Node lowestAncestor2(Node head, Node a, Node b) {
return process(head, a, b).ans;
}
public static class Info {
public boolean findA;
public boolean findB;
public Node ans; // 是否找到了答案的节点
public Info(boolean fA, boolean fB, Node an) {
findA = fA;
findB = fB;
ans = an;
}
}
public static Info process(Node x, Node a, Node b) {
if (x == null) {
return new Info(false, false, null);
}
Info leftInfo = process(x.left, a, b);
Info rightInfo = process(x.right, a, b);
boolean findA = (x == a) || leftInfo.findA || rightInfo.findA;
boolean findB = (x == b) || leftInfo.findB || rightInfo.findB;
Node ans = null;
if (leftInfo.ans != null) {
ans = leftInfo.ans;
} else if (rightInfo.ans != null) {
ans = rightInfo.ans;
} else {
//x就是答案
if (findA && findB) {//左数和右树都找到了
ans = x;
}
}
return new Info(findA, findB, ans);
}四派对的最大快乐值
多叉树代表公司结构的快乐值问题
4.1 描述
多叉树代表公司结构没人有个快乐值发请柬来参见聚会直接上下级的不能邀请返回最大的快乐值
公司的每个员工都符合 Employee 类的描述。整个公司的人员结构可以看作是一棵标准的、 没有环的多叉树。树的头节点是公司唯一的老板。除老板之外的每个员工都有唯一的直接上级。 叶节点是没有任何下属的基层员工(subordinates列表为空),除基层员工外,每个员工都有一个或多个直接下级。
派对的最大快乐值
这个公司现在要办party,你可以决定哪些员工来,哪些员工不来,规则:
1.如果某个员工来了,那么这个员工的所有直接下级都不能来
2.派对的整体快乐值是所有到场员工快乐值的累加
3.你的目标是让派对的整体快乐值尽量大
给定一棵多叉树的头节点boss,请返回派对的最大快乐值。
4.2 分析
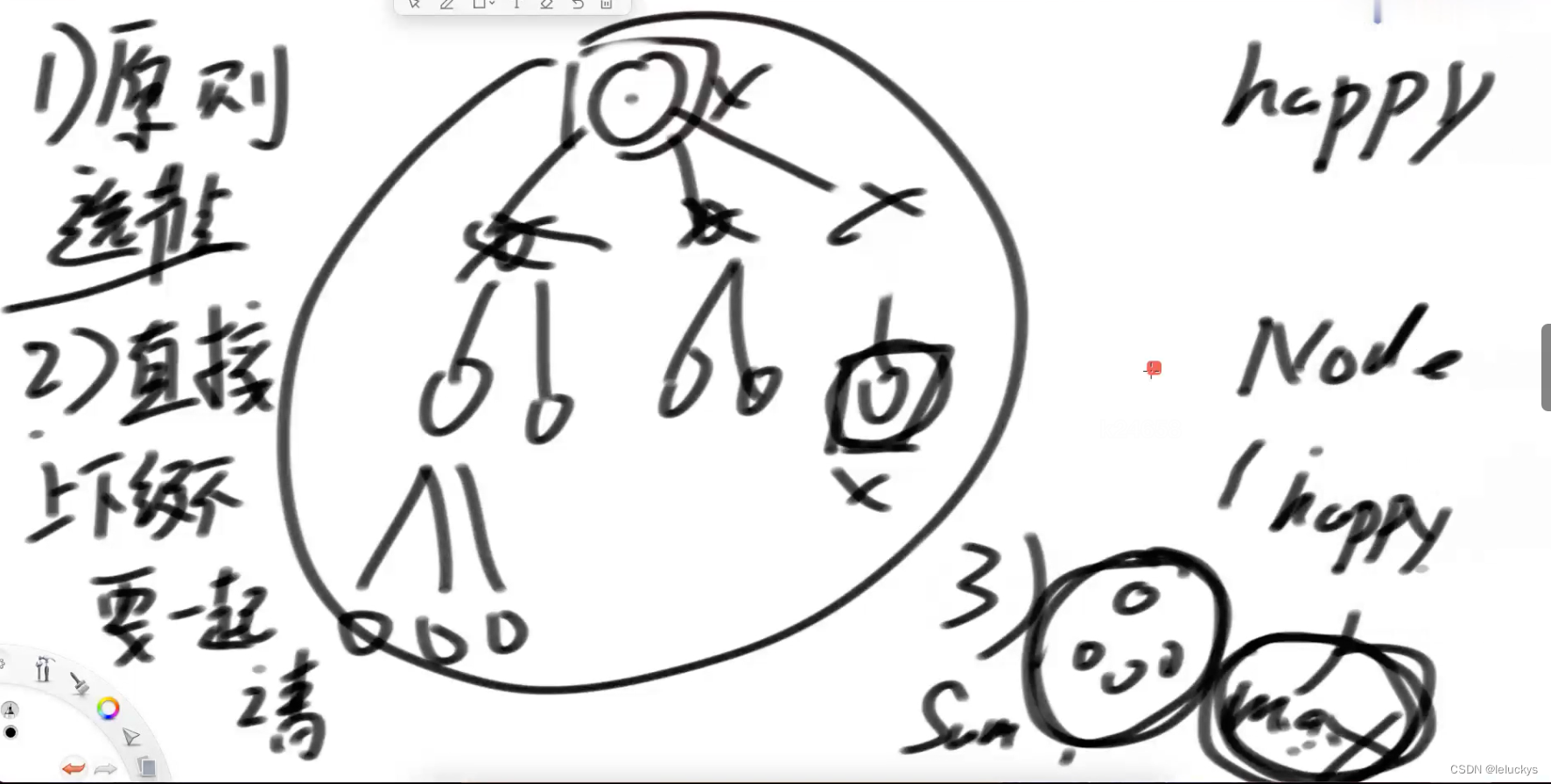
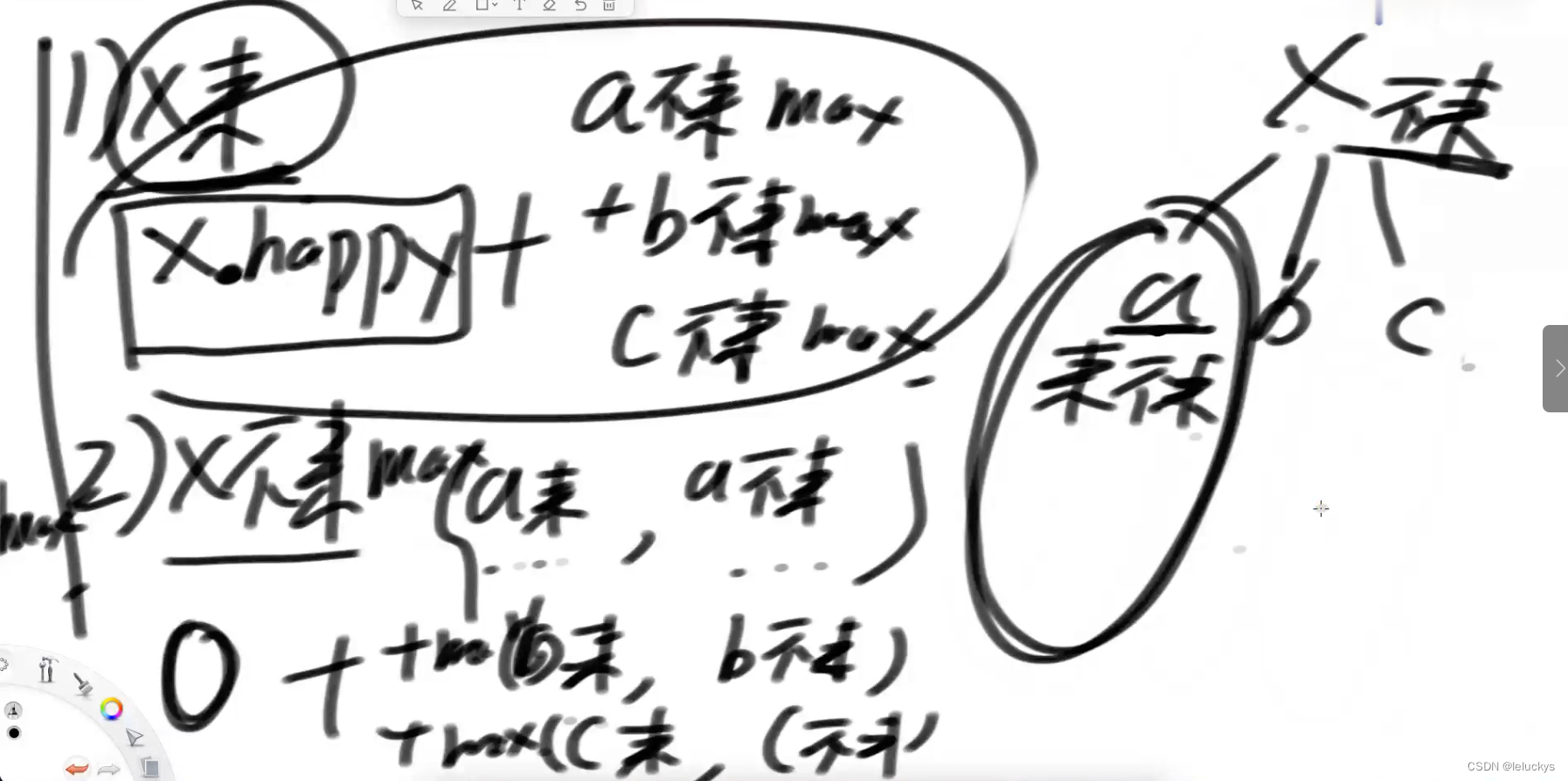
二叉树递归分析
需要收集的信息是来和不来的快乐值
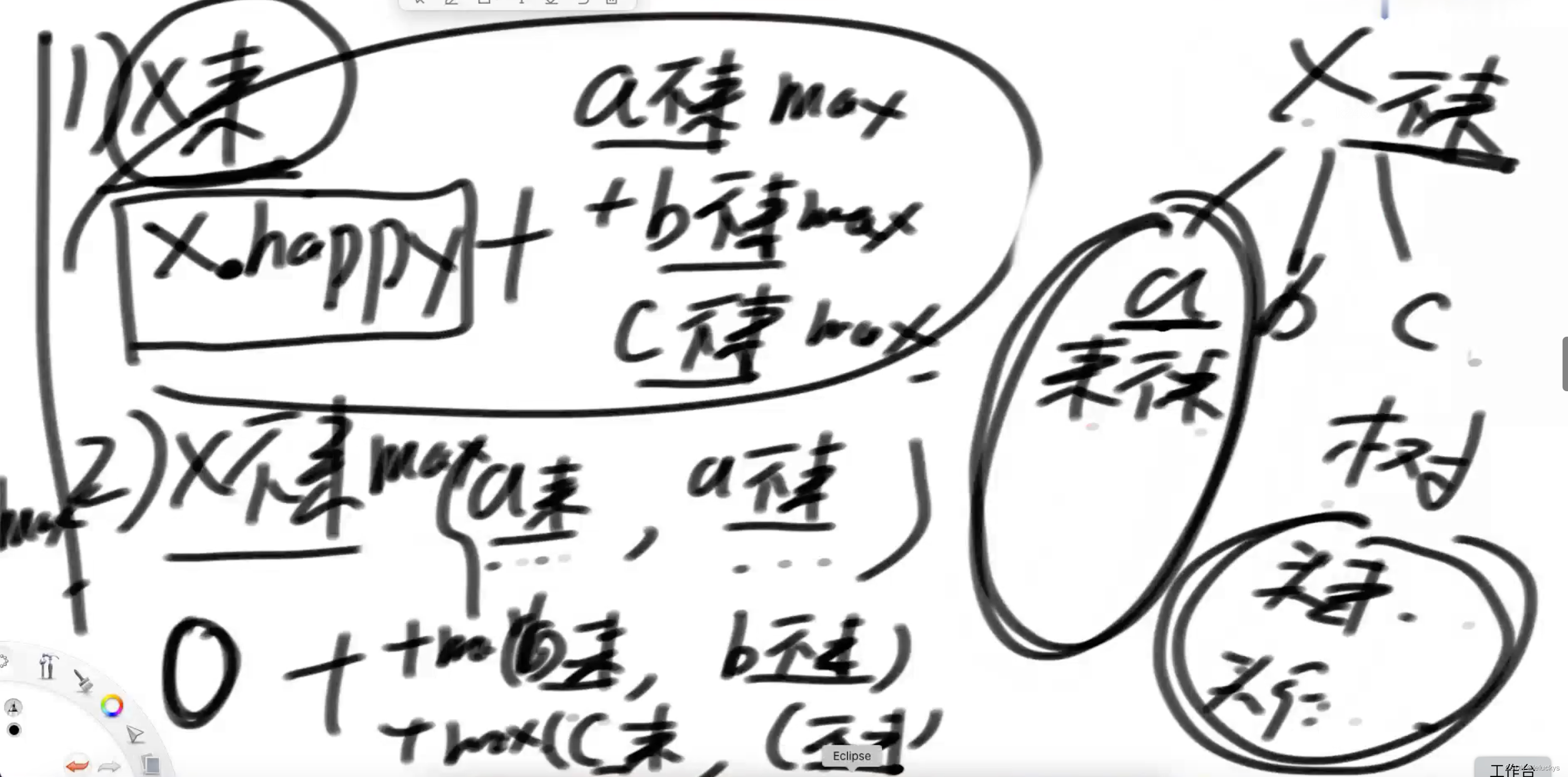
4.3 代码
public static class Employee {
public int happy;
public List<Employee> nexts;
public Employee(int h) {
happy = h;
nexts = new ArrayList<>();
}
}
public static int maxHappy1(Employee boss) {
if (boss == null) {
return 0;
}
return process1(boss, false);
}
// 当前来到的节点叫cur,
// up表示cur的上级是否来,
// 该函数含义:
// 如果up为true,表示在cur上级已经确定来,的情况下,cur整棵树能够提供最大的快乐值是多少?
// 如果up为false,表示在cur上级已经确定不来,的情况下,cur整棵树能够提供最大的快乐值是多少?
public static int process1(Employee cur, boolean up) {
if (up) { // 如果cur的上级来的话,cur没得选,只能不来
int ans = 0;
for (Employee next : cur.nexts) {
ans += process1(next, false);
}
return ans;
} else { // 如果cur的上级不来的话,cur可以选,可以来也可以不来
int p1 = cur.happy;
int p2 = 0;
for (Employee next : cur.nexts) {
p1 += process1(next, true);
p2 += process1(next, false);
}
return Math.max(p1, p2);
}
}
//二叉树的递归来收集快乐值
public static int maxHappy2(Employee head) {
Info allInfo = process(head);
return Math.max(allInfo.no, allInfo.yes);
}
public static class Info {
public int no;
public int yes;
public Info(int n, int y) {
no = n;
yes = y;
}
}
public static Info process(Employee x) {
if (x == null) {
return new Info(0, 0);
}
int no = 0;
int yes = x.happy;
for (Employee next : x.nexts) {
Info nextInfo = process(next);
//先一个节点可以选可以不选,选择他们当中的最大值
no += Math.max(nextInfo.no, nextInfo.yes);
yes += nextInfo.no;
}
return new Info(no, yes);
}