作者：Kartik Chandra
单位：MIT
官网链接：Github

下面将首先以简单翻译文章重要内容，穿插一些讲解，并进行简单的复现实验。之后总结各种资料，如review意见等。最后讲解代码，研究具体实现。

文章讲解

摘要

1、基于梯度下降的机器学习算法需要有很多超参数需要调节，如学习率，优化器参数(动量等)。
2、可以手动导出超参数梯度的表达式，通过反向传播与模型一起优化。
3、本文将展示通过自动微分(AD, Automatic Differentiation)方法，自动计算超梯度。
4、还可以实现递归超参数，即超参数，超超参数，超超超参数等的自动优化。递归层数越多，网络对初始超参数选择越不敏感。
5、通过MLP分类MINIST，ResNet20分类CIFAR10，LSTM分类Tolstoy三个实验进行验证。

1 介绍

对于网络训练的学习率设置，过大不易收敛甚至发散，过小收敛很慢。Baydin[1]手动设计超参数梯度表达式进行超参数优化，可以提升末端收敛性，当初始参数不是最优时表现较好。

上述方法三个缺点：
1、手工设计容易出错，且需要针对每个优化器重新设计，如SGD的学习率一个参数，Adam的学习率动量等多个参数等。
2、只能调学习率，不能调动量等。
3、引入了新的超超参数，即学习率的学习率，这个也得能调。

本文使用自动微分AD解决上述问题，有如下三个优点：
1、不需要手动设计，自动求微分。
2、同时处理学习率，动量等超参数。
3、可以递归处理超超参数，超超超参数等([1]假设过，但复杂度过高没有实现)。

自动微分与编程语言中的lambd表达式相关。第二节讲实现细节，第三节将实验。

2 实现细节

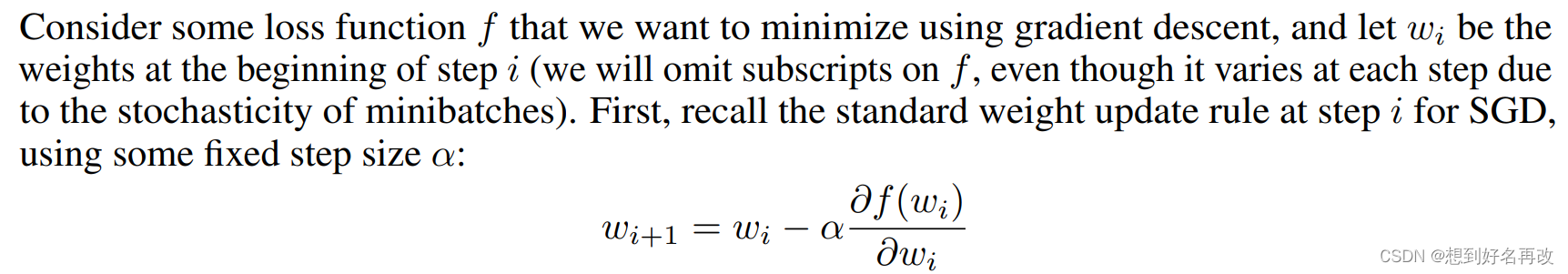
上式为简单的随机梯度下降算法表达式，$f$为损失函数，$w_i$为时刻$i$的权重，$\alpha$为学习率，更新过程即为第$i$时刻的权重减去学习率乘损失函数对权重的偏导，得到的结果即为新的权重。

现在希望学习率可以随着权重一起更新，即将原本的单权重更新改为先更新学习率，再更新权重。

学习率的更新公式如公式(1)所示，引入了超超参数(学习率的学习率)，通过损失对学习率求偏导更新学习率。

所以过程转换为求公式(1)中学习率的更新量，即$\frac{\partial f(w_i)}{\partial {\alpha }_i}$。

2.1 手动计算$\frac{\partial f(w_i)}{\partial {\alpha }_i}$

[1]中提供而计算方法如公式3~4所示，公式3根据链式求导法则转化为公式4的形式，通过保留$i$和$i-1$时刻的梯度，表示$i$时刻损失学习率的梯度。

根据上述方法可以将SGD中的学习率梯度推广到Adam中的学习率和动量等。

上述即为Adam中所有参数的梯度表达式。

2.2 自动微分

自动微分机制首先在前向传播计算损失时保留计算图(pytorch框架正常的前向传播都会保存)，再根据计算图反向传播误差。比如有有向图G，G的根节点为损失，叶子结点为权重，中间的结点为计算过程，边表示依赖关系。前向传播根据网络设计建立图，反向传播再根据建立的图计算梯度，保存到叶子结点上，然后更新权重，进行迭代。
为方便理解可见如下示意图：

上图所示即为简单的前向传播计算图，$w_1$和$w_2$表示权重，$X$表示输入数据，$pred$表示网络输出，$Y$表示标签，$loss$表示最终的损失，该网络公式为：
$pred=w_1\ast (w_2+X)$
其损失定义为：
$loss=Y-pred$

每一次迭代之前需要清空计算图，否则下一次反向传播将会累计梯度，使其线性增长(人话：optim.zero_grad()，先detach再置零，说的是detach那一步，可以参考这篇文章的讲解optimizer.zero_grad())。示意图如图1(a)所示：



上述代码显示的标注了传统SGD进行oprim.zero_grad()中detach的那一部分。self.alpha.detach()等价于self.alpha.no_grad()，即传入的alpha就是不带梯度的，学习率不随反向传播更新。

然后是学习率可更新的版本，参考前面的公式，其中，alpha有梯度，先更新alpha，再用更新的alpha更新权重，如图1(b)所示。

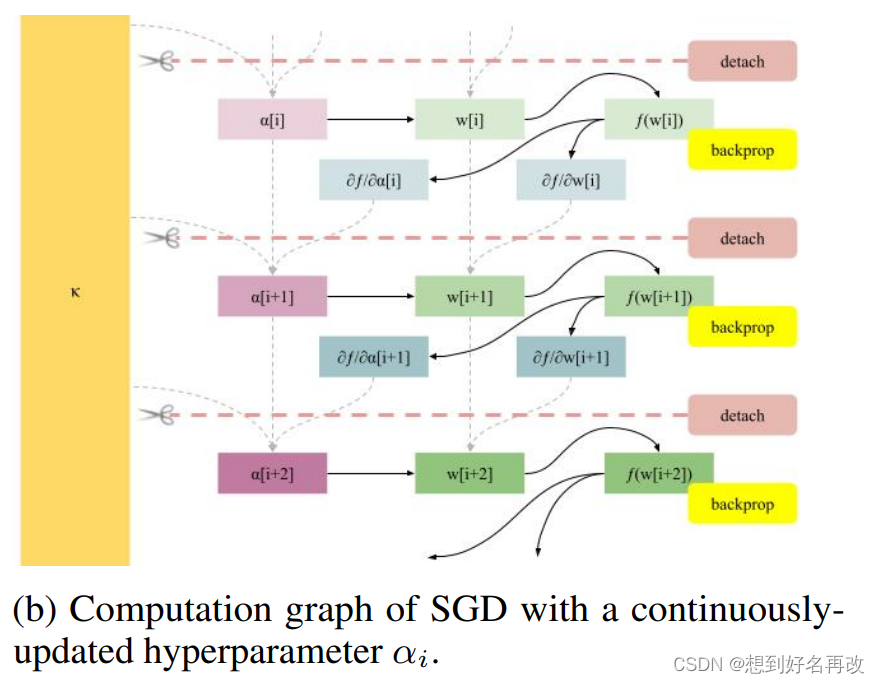
2.3 扩展到其他优化器

上述步骤可以很容易的扩展到Adam等优化器。

2.4 超优化器堆叠(超超优化器，超超超优化器，。。。。)

超优化器理论上可以无限递归[1]。如下伪码所示，表示使用SGD优化alpha，再进行权重更新，即SGD套SGD的递归超优化。

上述递归可以用另一种形式表示，即通过传参指定alpha使用的优化器，即可以是SGD套SGD，也可以是Adam套SGD。

最终的优化器代码形式如下：

HyperSGD(0.01, HyperSGD(0.01, SGD(0.01)))

表示三层SGD递归。同时[1]中指出，递归越多对初始参数的选择越不敏感，后续将通过实验验证。

3 实验

内容：单层超参数调整和多层堆叠
设备：Titan Xp

3.1 SGD超优化实验

实验设置：
1、网络结构：两层全连接，隐藏层为128，10分类，tanh激活。
2、参数设置：Batch size为256，30epoch，学习率0.01，重复三次。
实验目的：
1、超优化SGD是不是比SGD好。
2、最终的学习率是不是比人类选择的好(用一个超优化SGD学一个学习率，然后再用正常SGD和学到的学习率训练)。
具体结果如表1(a)所示：


其中，左边表示模型的优化器，斜杠右边为学习率超优化器。
结果：
1、使用超优化比SGD有提升。
2、使用超优化学到的参数重新训练比原来的参数好。

3.2 对于其他优化器(Adam，AdaGrad，RMSProp)参数的超优化实验

实验设置：与3.1网络结构相同，参数除了epoch为5(说是防止过拟合)，学习率为0.001， β1=0.9, β2=0.99，其他相同。
实验目的：
1、超参数Adam是否比其他的好(同3.1)。
2、学到的超参数是否比原来的好(同3.1)。
3、只优化学习率还是动量等也优化。


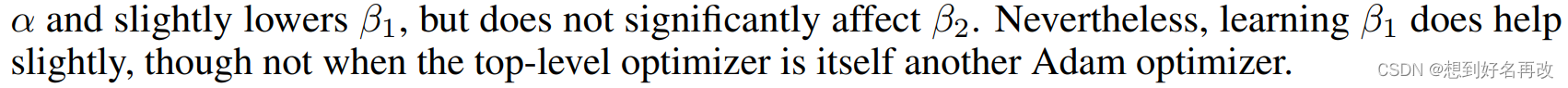
实验结果如图1(b)所示：

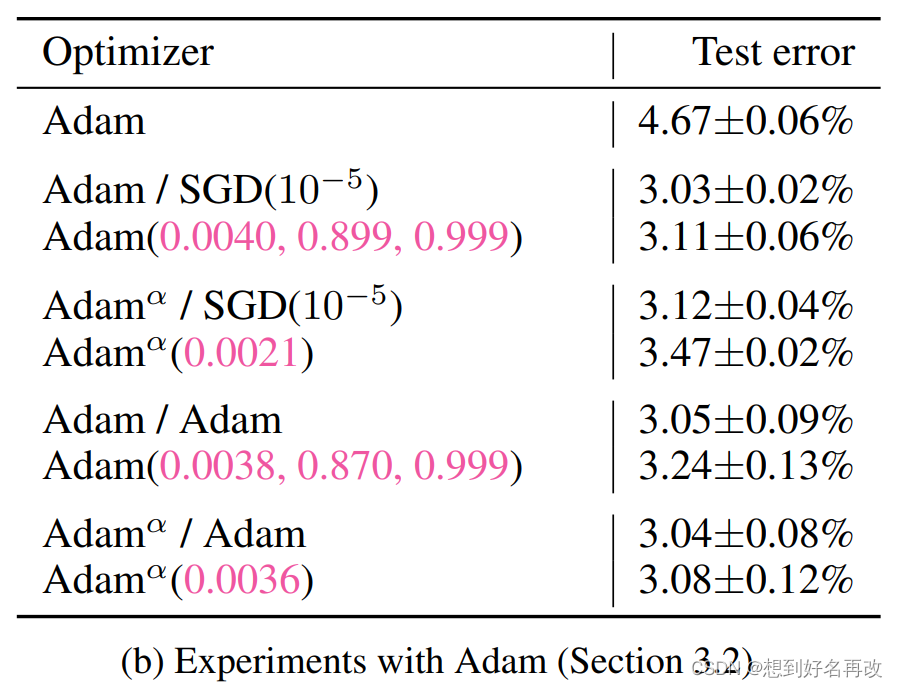
结果：
1、超优化Adam比原来的Adam好(同3.1)
2、学到的比原来的好(同3.1)
3、默认学习率为0.001
3.1、SGD优化所有参数时，学习率有提升，两个β变化不明显。
3.2、SGD只优化学习率时，学习率有提升。
3.3、Adam优化所有参数时，学习率有提升，β1下降但不多。
3.4、Adam只优化学习率时，学习率有提升。


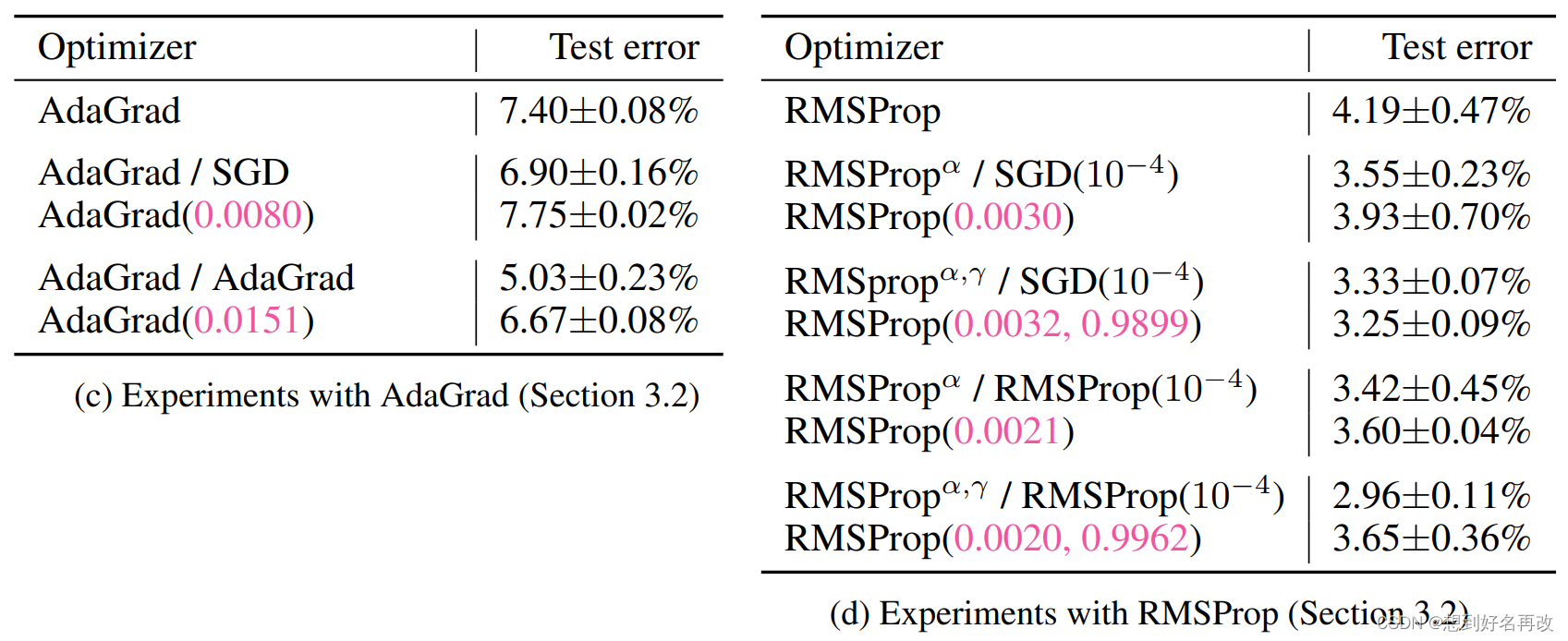
表1(c )和(d)结果与(b)相似。

3.3 大规模超优化

3.3.1 ResNet20

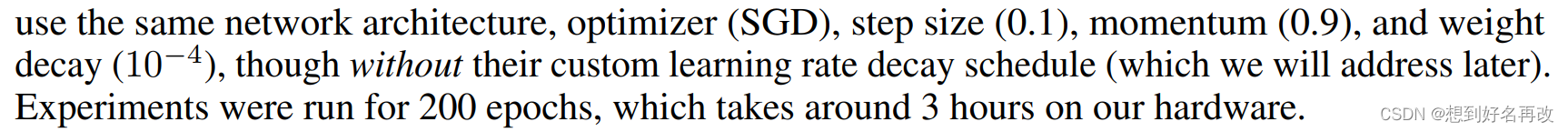
数据集：CIFAR-10
参数：学习率0.1，动量0.9，weight_dacay0.0001，但！！！没有用学习率调整器，即学习率始终固定，epoch为200，训练时长3h。


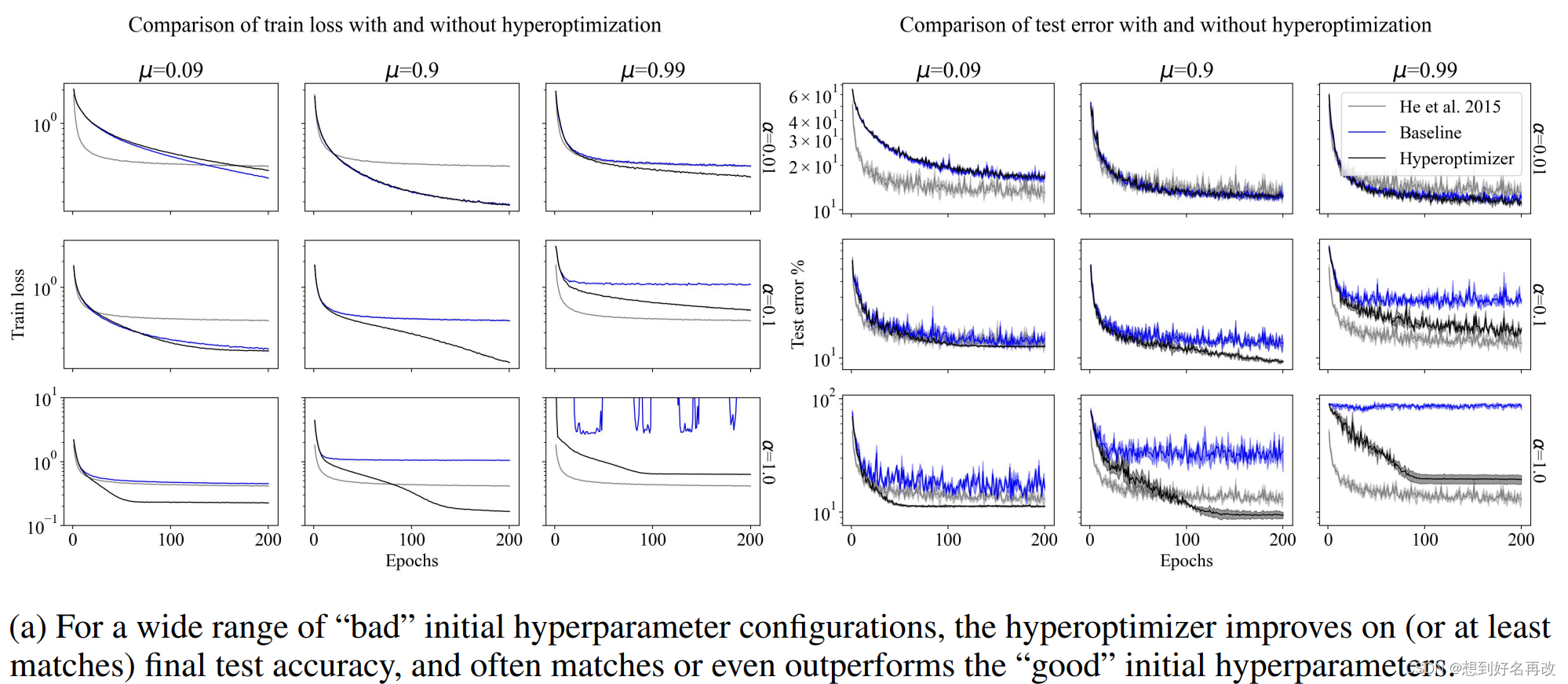
设置了不同程度的初始学习率和动量，即过小、合适、过大，同时设置了超优化器。结果如图2(a)所示，超优化的效果基本上都超过或者等同于最优设置(此处最优设置为不使用学习率调整器的情况，即固定超参数)，但当参数同时过大或过小时，效果不好。


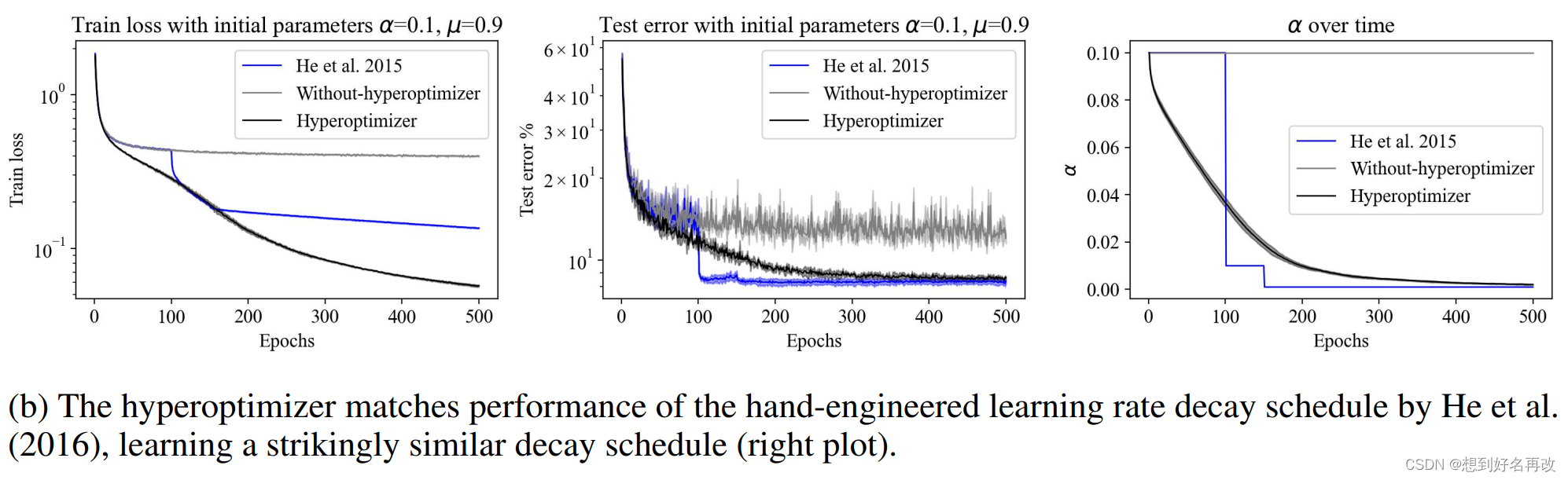
之后还尝和学习率调整器做了对比，初始学习率与ResNet原文中相同，均为0.1，SGD中动量设置为0.9，weight_dacay设置为0.0001，结果如图2(b)。超优化和非固定学习率取得相似结果，均远好于固定学习率。

3.3.2 RNN

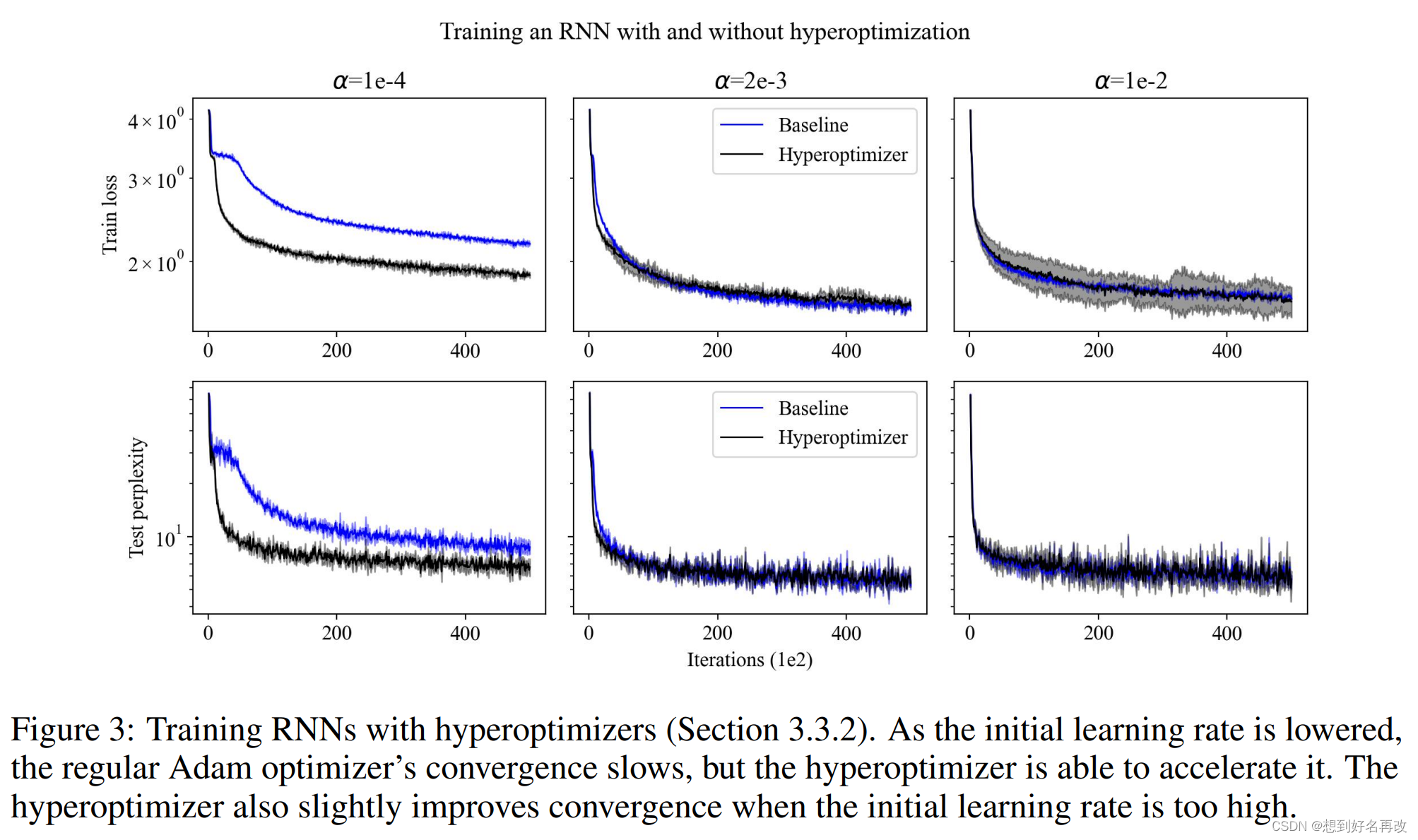
结果与CNN相似。

3.4 多层超优化(超超，超超超优化)

[1]预测多层超优化对较差的初始参数更友好。我们的实验发现，大型网络层数较深，如ResNet20和RNN，在初始学习率较大时会发散，所以使用逐渐递减的学习率初始化(具体怎么设置没看懂。。。。)

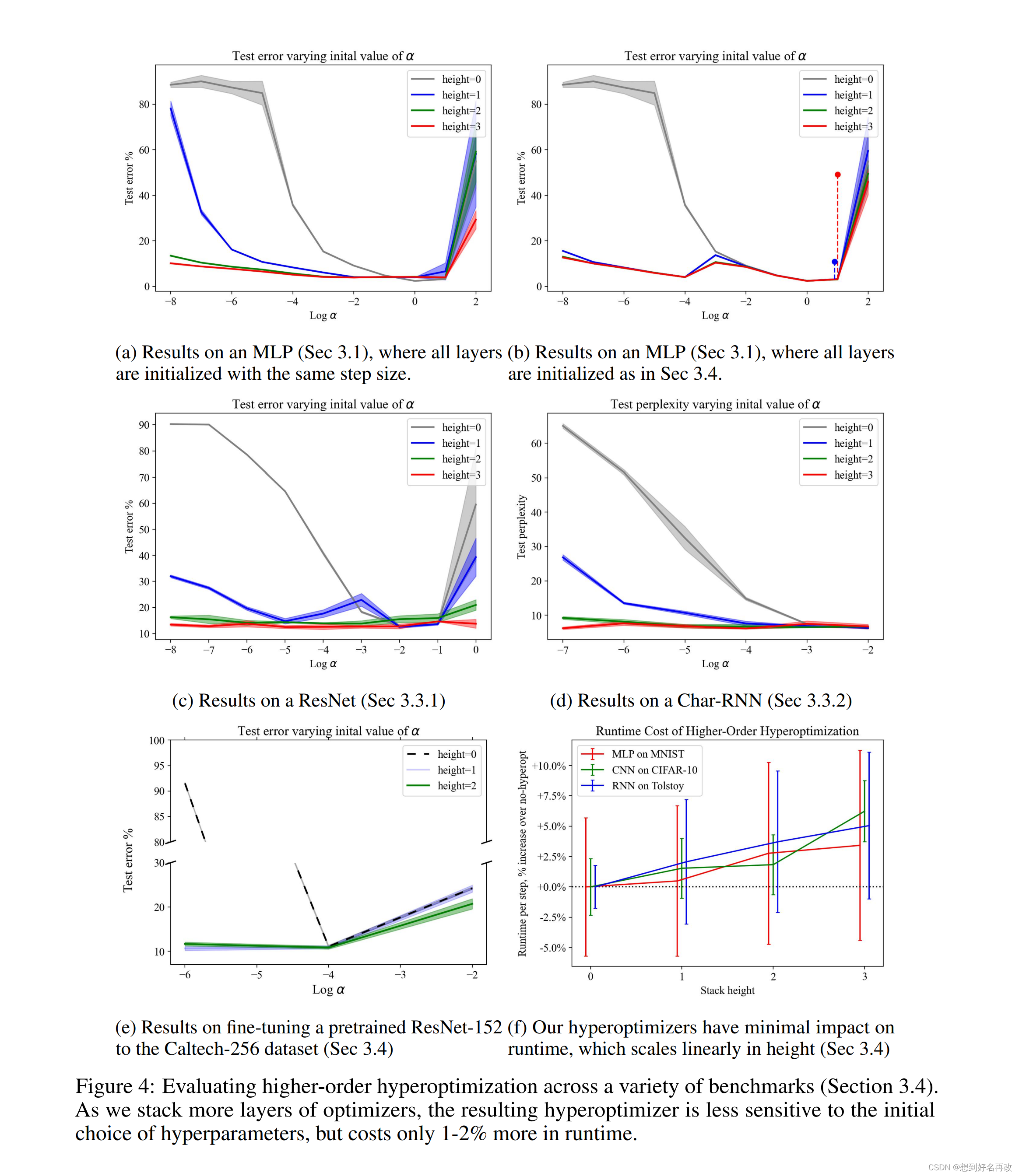
结果如图4，即层数越多对初始选择越不敏感，且计算代价增长不大(多一层增加1-2%)。

4 相关工作

2019年综述[2]，2017年收敛性分析[3]。之前的工作大部分使用几次迭代的梯度计算超参数的梯度，计算代价较大。[1]可以实现每一步更新超参数。
本文在三方面提出改进：
1、超参数梯度全自动化计算，不用手动计算
2、不仅优化学习率
3、多层超优化器
我们的多层超优化器可能使初始学习率选择的难度降低。

5 限制

缺点：
1、参数设置过高或过低还不能处理，需要进一步优化。
2、对框架的实现细节要求较高，如梯度的detach和计算图保留等。
影响：
可以帮助搜索参数。

6 结论

ref

[1] A. G. Baydin, R. Cornish, D. M. Rubio, M. Schmidt, and F. Wood. Online learning rate adaptation with hypergradient descent. In Sixth International Conference on Learning Representations (ICLR), Vancouver, Canada, April 30 – May 3, 2018, 2018.
[2] M. Feurer and F. Hutter. Hyperparameter Optimization, pages 3–33. Springer International Publishing, Cham, 2019. ISBN 978-3-030-05318-5. doi: 10.1007/978-3-030-05318-5_1. URL https://doi.org/10.1007/978-3-030-05318-5_1.
[3] D. M. Rubio. Convergence analysis of an adaptive method of gradient descent. University of Oxford, Oxford, M. Sc. thesis, 2017. URL https://damaru2.github.io/convergence_analysis_hypergradient_descent/dissertation_hypergradients.pdf.

其他资料

参考openreview中关于本文章的意见。
总结如下：
1、创新性不足，主要工作[1]已完成，本文实验为主。
2、文章的一些小缺陷以及消融实验和扩展实验。
3、文章主要在小规模数据集和小网络上做实验，不符合现在主流深度学习方法，且作者可以避开这方面的对比。

Reviewer1

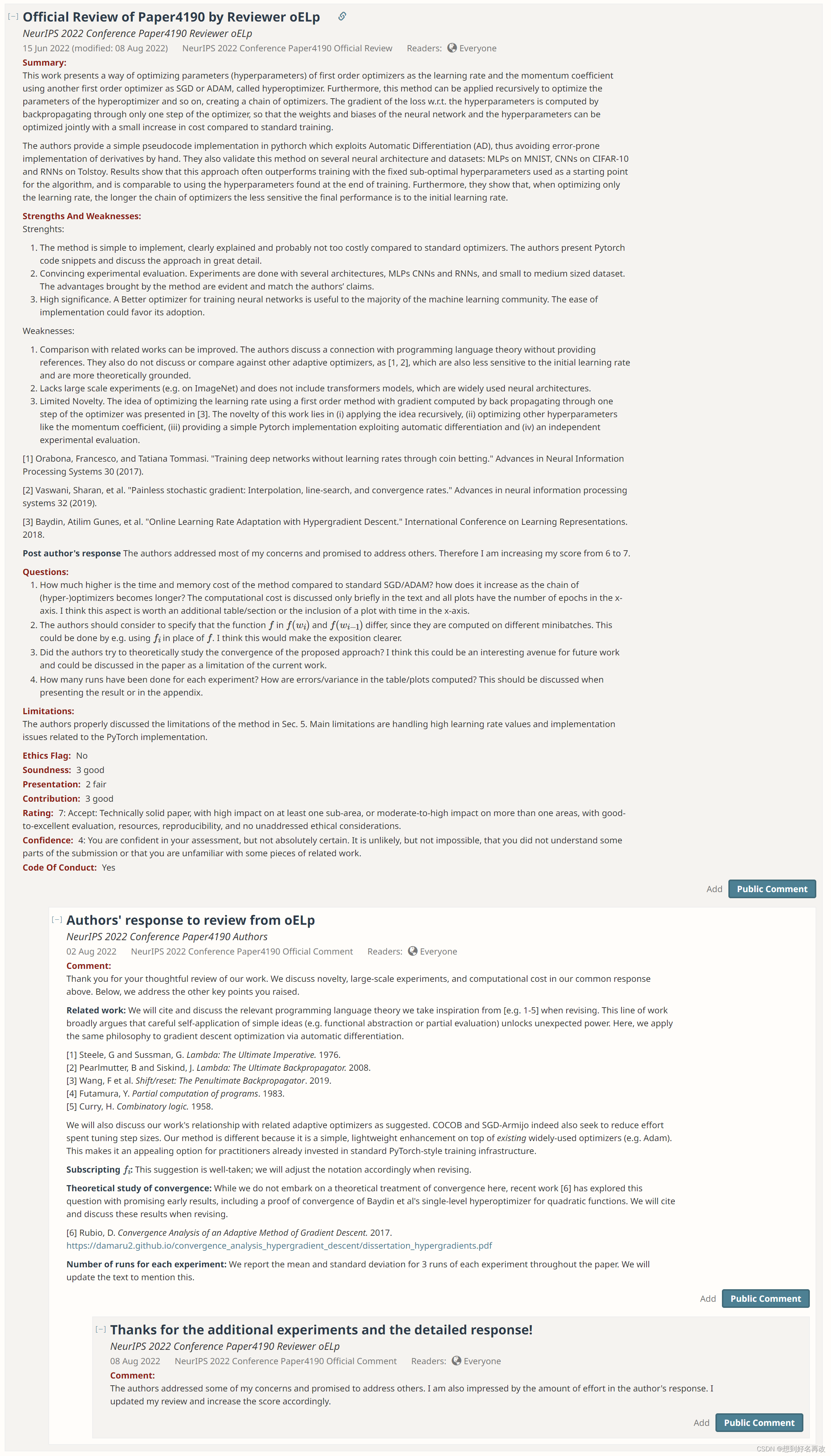
优势：
1、方法简单，计算代价较低
2、多种实验，较为充分
3、有潜在应用价值
缺点：
1、没有和其他超优化方法进行对比，只是自己做了消融实验
2、只在小型数据集进行实验，缺乏大型试验，如ImageNet
3、创新性有限：[1]以及做了大部分基础工作，本文只是在基础上进行了一些延伸如递归优化和其他超参数优化
4、缺乏理论分析和证明

Reviewer2

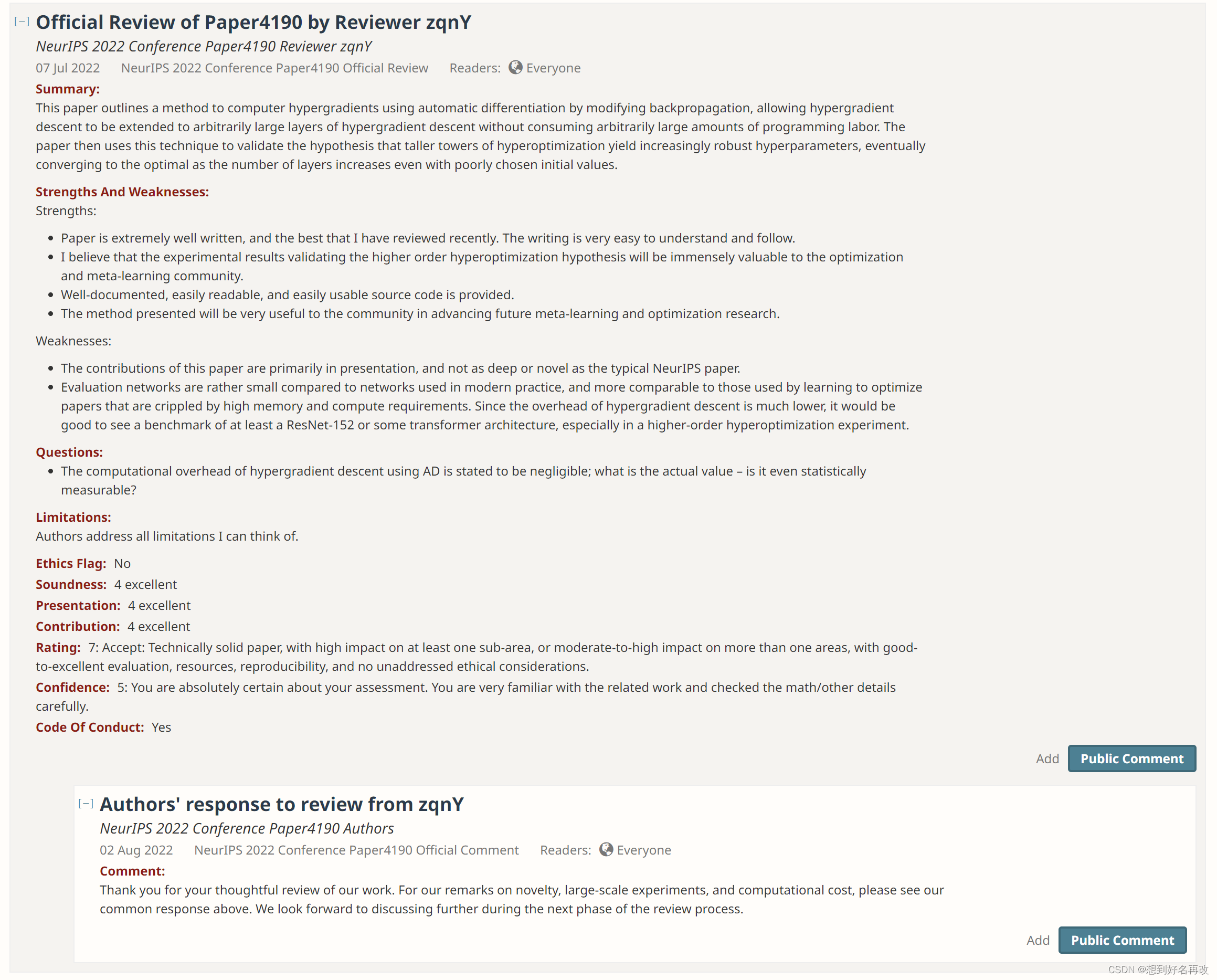
优势：
1、方法简单易懂
2、研究意义较大
缺点：
1、新颖性不足
2、实验规模不足，缺少如ResNet152和Transformer等大模型的实验

Reviewer3

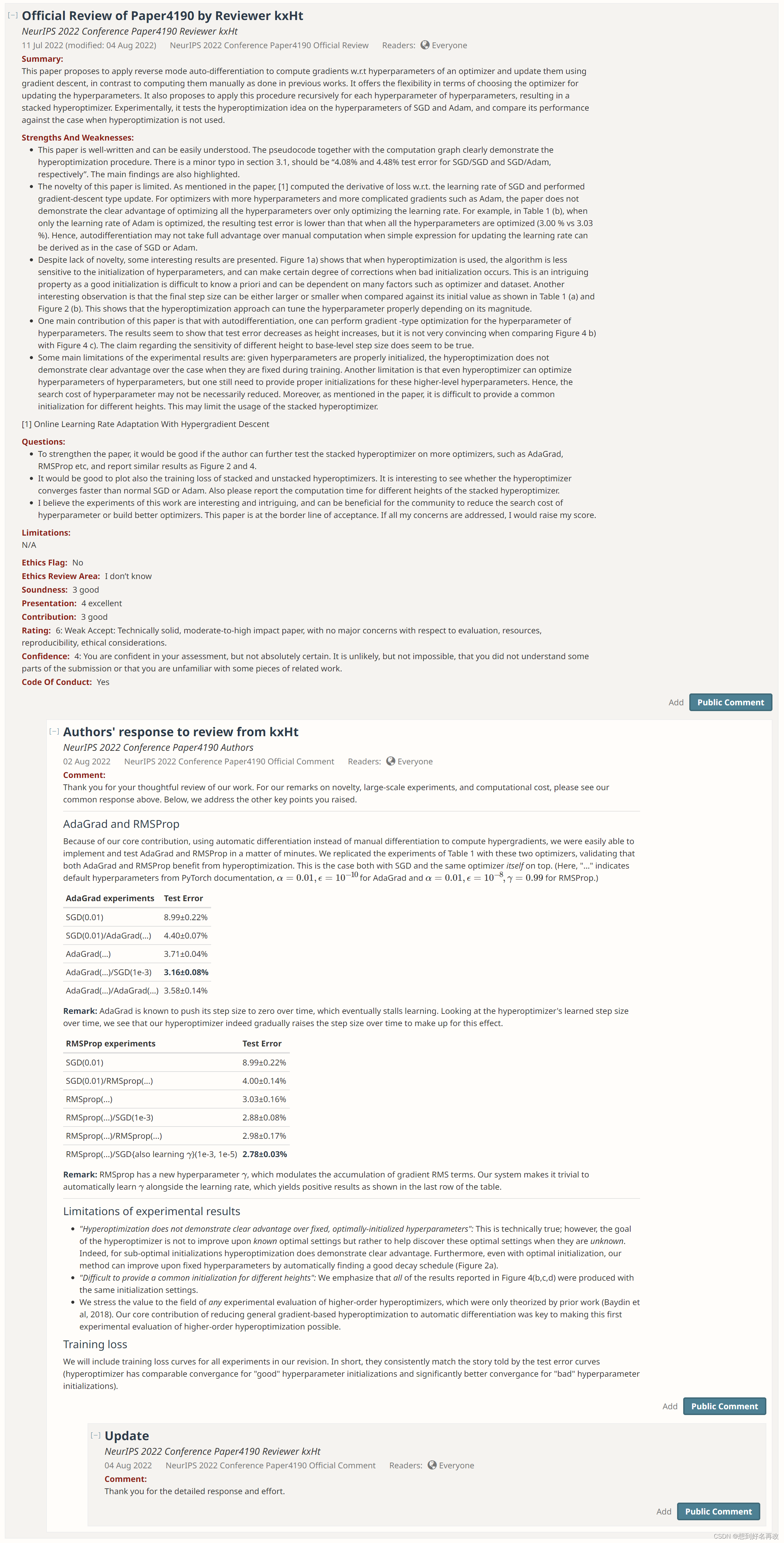
优势：
1、文章通俗易懂
2、文章中的堆叠超优化可能有潜在用处，因为初始参数不易确定，可以堆叠多层自动搜索
不足：
1、新颖性较低，主要工作[1]已完成，本文主要是实验实现
2、添加loss图，不同优化器的对比等(预印版已添加)

For All Reviewers

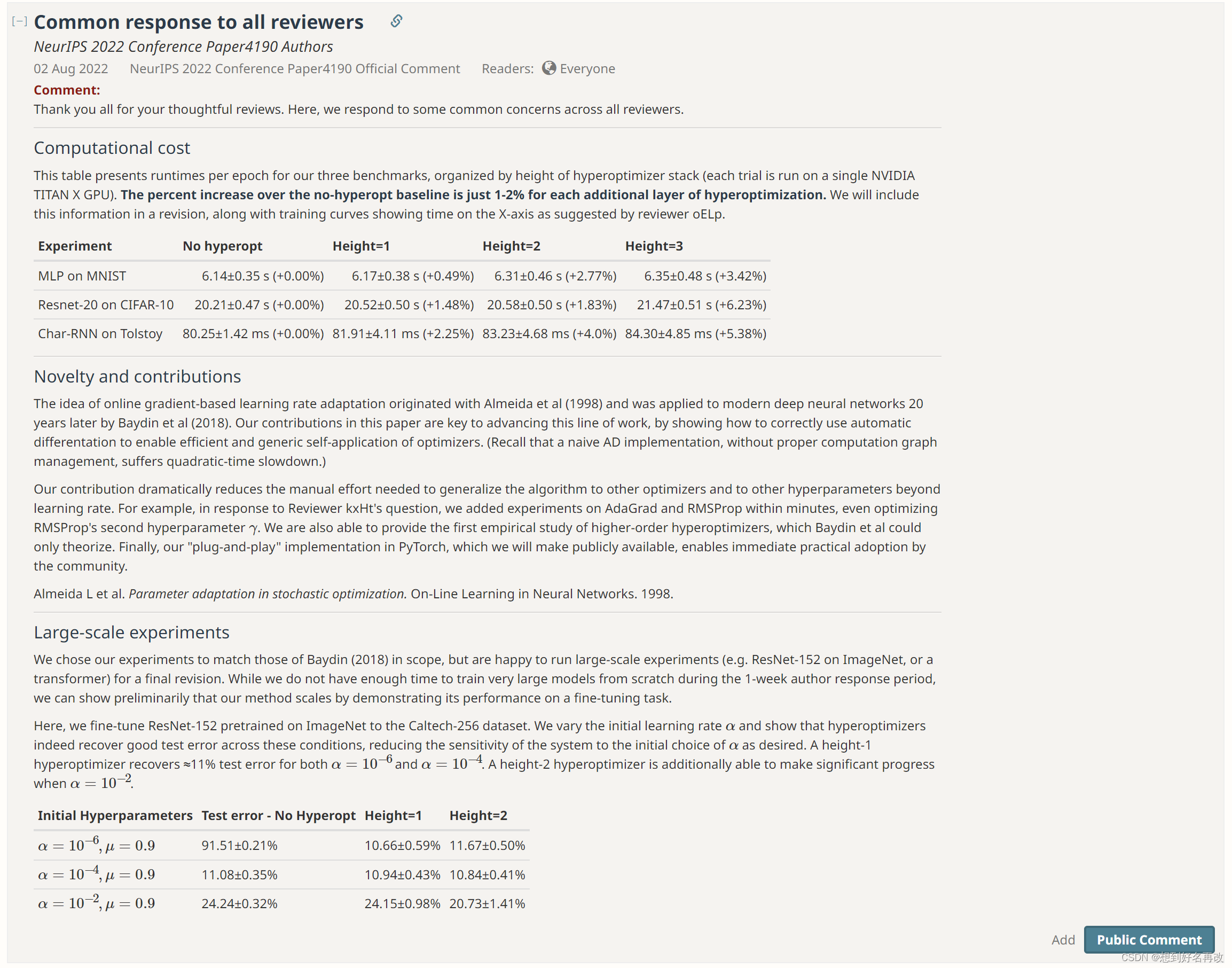
内容补充：在文中补充了关于训练时间随优化器层数增加的变化图。
关于创新性：本文延伸了[1]的工作，使其可以应用到更多优化器和网络上，简化流程，做到即插即用(感觉还是实验为主)
大规模实验：做了一个迁移与训练实验，结果表明，超优化学习率精度高于固定学习率微调。(虽然数据集256类，但仍然是中小型数据集，作者刻意避开了大规模数据集以及重新训练，所以审稿人3并没有调整分数)

Final Decision

最终决定accept，分数为776，7为accept，6为weak accept。

代码讲解及实验

TBD