62. 不同路径,66. 加一,67. 二进制求和,每题做详细思路梳理,配套Python&Java双语代码, 2024.03.21 可通过leetcode所有测试用例。
目录
62. 不同路径
解题思路
完整代码
Python
Java
66. 加一
解题思路
完整代码
Python
Java
67. 二进制求和
解题思路
完整代码
Python
Java
62. 不同路径
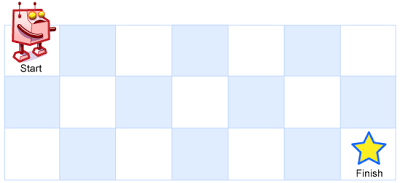
一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7 输出:28示例 2:
输入:m = 3, n = 2 输出:3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下示例 3:
输入:m = 7, n = 3 输出:28示例 4:
输入:m = 3, n = 3 输出:6
解题思路
通过动态规划(Dynamic Programming,DP)来解决。动态规划是一种将复杂问题分解成更小子问题的方法,通过解决这些子问题,我们可以解决整个问题。
-
定义状态: 我们定义
dp[i][j]为到达网格中(i, j)位置的不同路径的数量。其中,i表示行索引,j表示列索引。 -
状态转移方程: 考虑到机器人每次只能向下或向右移动,那么到达某个点
(i, j)的路径只能通过左边的点(i, j-1)或上面的点(i-1, j)来达到。因此,我们可以得出状态转移方程为dp[i][j] = dp[i-1][j] + dp[i][j-1]。 -
初始化: 网格的最上方和最左侧的路径数都为1,因为从起点到这些点只有一条路径。即,对于所有的
i和j,dp[i][0] = 1和dp[0][j] = 1。 -
计算顺序: 从左上角开始,逐行或逐列填充
dp表格,直到达到右下角。 -
返回结果: 最终结果即为
dp[m-1][n-1],表示到达右下角的不同路径数量。
完整代码
Python
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
dp = [[1]*n for _ in range(m)] # 初始化dp表格
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i-1][j] + dp[i][j-1] # 状态转移
return dp[-1][-1] # 返回右下角的路径数量Java
public class Solution {
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
// 初始化最上方和最左侧的路径数量为1
for (int i = 0; i < m; i++) {
dp[i][0] = 1;
}
for (int j = 0; j < n; j++) {
dp[0][j] = 1;
}
// 填充dp表格
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i-1][j] + dp[i][j-1]; // 状态转移
}
}
return dp[m-1][n-1]; // 返回结果
}
}
66. 加一
给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
示例 1:
输入:digits = [1,2,3] 输出:[1,2,4] 解释:输入数组表示数字 123。示例 2:
输入:digits = [4,3,2,1] 输出:[4,3,2,2] 解释:输入数组表示数字 4321。示例 3:
输入:digits = [0] 输出:[1]
解题思路
这个问题的核心在于处理数字加一导致的进位问题。特别是当数组中的数字全部为9时,加一操作会导致数组长度增加。
-
从后向前遍历数组: 因为加一操作只影响低位,所以我们从数组的最后一个元素开始向前遍历。
-
处理加一操作: 对于数组的每个元素,我们将其加一然后取模10,这样如果当前位是9,加一后会变成0。如果加一后不为0,表示没有进位,直接返回结果。
-
处理进位: 如果到达数组的第一个元素还存在进位,我们需要在数组最前面添加一个元素1。
完整代码
Python
class Solution:
def plusOne(self, digits: List[int]) -> List[int]:
n = len(digits)
for i in range(n-1, -1, -1): # 从后向前遍历
digits[i] += 1
digits[i] %= 10
if digits[i] != 0: # 如果不等于0,说明没有进位,直接返回
return digits
# 如果所有位都进位了,说明是类似于99,999这样的数字,需要在最前面加一个1
return [1] + digitsJava
public class Solution {
public int[] plusOne(int[] digits) {
for (int i = digits.length - 1; i >= 0; i--) { // 从后向前遍历
digits[i]++;
digits[i] = digits[i] % 10;
if (digits[i] != 0) return digits; // 如果不等于0,说明没有进位,直接返回
}
// 如果所有位都进位了,说明是类似于99,999这样的数字,需要在最前面加一个1
int[] newDigits = new int[digits.length + 1];
newDigits[0] = 1;
return newDigits;
}
}
67. 二进制求和
给你两个二进制字符串
a和b,以二进制字符串的形式返回它们的和。示例 1:
输入:a = "11", b = "1" 输出:"100"示例 2:
输入:a = "1010", b = "1011" 输出:"10101"
解题思路
-
初始化:定义一个字符串
result用来存放结果,carry变量存放进位,初始值为0。同时,定义两个指针i和j分别指向a和b的末尾。 -
逐位相加:从末尾开始向前遍历字符串
a和b,逐位相加,并加上前一位的进位carry。每一位的结果是(a[i] - '0') + (b[j] - '0') + carry。这里a[i] - '0'是为了将字符转换为其对应的数字。 -
计算当前位和新的进位:当前位的结果是相加结果对2取余(
(sum % 2)),进位是相加结果除以2的商(sum / 2)。 -
更新结果字符串:将当前位的结果转换为字符后加到
result的前面。 -
处理较长字符串的剩余位:如果
a或b中有剩余位未处理完,需要继续将剩余位加上进位,逐位处理,直到所有位都处理完毕。 -
处理最高位的进位:如果最后还有进位(
carry不为0),需要将进位加到结果的最前面。 -
返回结果:返回
result字符串。
完整代码
Python
class Solution:
def addBinary(self, a: str, b: str) -> str:
i, j, carry = len(a) - 1, len(b) - 1, 0
result = []
while i >= 0 or j >= 0 or carry:
sum = carry
if i >= 0:
sum += int(a[i])
i -= 1
if j >= 0:
sum += int(b[j])
j -= 1
carry = sum // 2
result.append(str(sum % 2))
return ''.join(result[::-1])Java
public class Solution {
public String addBinary(String a, String b) {
StringBuilder result = new StringBuilder();
int i = a.length() - 1, j = b.length() - 1, carry = 0;
while (i >= 0 || j >= 0 || carry > 0) {
int sum = carry;
if (i >= 0) sum += a.charAt(i--) - '0';
if (j >= 0) sum += b.charAt(j--) - '0';
result.insert(0, sum % 2);
carry = sum / 2;
}
return result.toString();
}
}