前置知识
蓝桥杯并查集|路径压缩|合并优化|按秩合并|合根植物(C++)-CSDN博客

可撤销并查集

关键注意

1. 可撤销并查集的撤销功能如何实现
2. 可撤销并查集能不能用路径压缩
   可撤销并查集(Reversible Union-Find)是一种扩展了标准并查集(Union-Find)数据结构的数据结构，它允许在进行连接(union)和查询(Find)操作的同时，能够回退(Undo)或者撤销之前的操作。这种数据结构通常用于支持一些需要回滚操作的应用，比如在离线算法中或者需要进行回退的决策问题中。当然主要是应用于在线算法，因为离线算法反悔可以完全输入后在一起处理。

举例

在蓝桥王国中有n个城市，王国经常会发生地震，会导致道路塌方，好在王国科技水平比较高也就只有刚修建好的道路会塌方，王国的人们出行前会询问两个地点是否连通。所以，你需要维护一棵动态森林，初始时包含n个散点，每个点代表一个独立的集合。然后，有m个操作，支持以下三种操作:连接操作(类型1):执行操作“1 u v”，将点u和点v连接起来，形成一个道路。这表示两个点之间有一条路。
查询操作(类型2):执行操作“2 u v”，用来査询点u和点v之间是否连通。如果它们在联通，输出"Yes"，否则输出“NO"
撤销操作(类型3):执行操作"3"，用于撤销上一个操作。这个操作需要保证存在被撤销的操作，即必须有之前的连接操作被撤销。

分析

我们采用并查集来表示联通，类似于最小生成树Kruskal算法，这样我们很容易就能完成op1和op2这两个操作。
但是第三个操作，如何去处理呢，怎么撤回呢，我们先不考虑路径压缩和启发式合并的情况下。并查集的合并为:
Fa[Find(i)]=j，我们只需要用变量记录t=Find(i)和m=Fa[Find(i)]即可。当反悔的时候我们直接Fa[t]=m即可。

但是既没有做路径压缩，又没有做启发式合并，那么查询效率是非常低的，所以我们很难通过一些复杂的题目。
所以我们还是需要去再去考虑优化办法。

路径压缩

我们考虑可不可以使用路径压缩来优化并查集。核心在于能够解决撤销上一步的能力。
我们考虑如果使用路径压缩优化后还能够撤销吗?
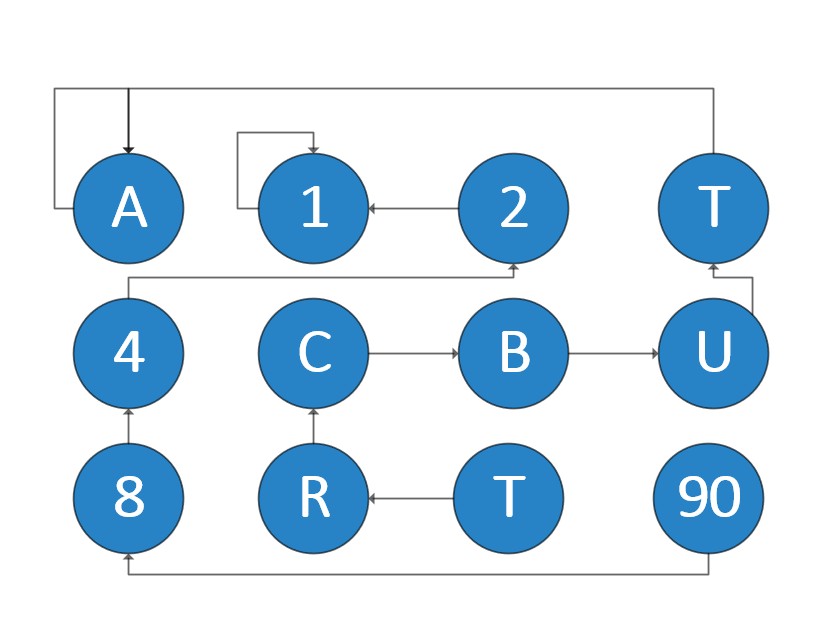
我们考虑这样一个图:
这样进行撤销的时候我们很容易记得上次操作的是什么，Fa[Find(i)]=j，我们只需要用变量记录t=Find(i)和m=Fa[Find(i)]即可。当反悔的时候我们直接Fa[t]=m即可。按照我们刚才考虑的就行，那如果是路径压缩之后对于路径压缩之后的右图还能否恢复呢?

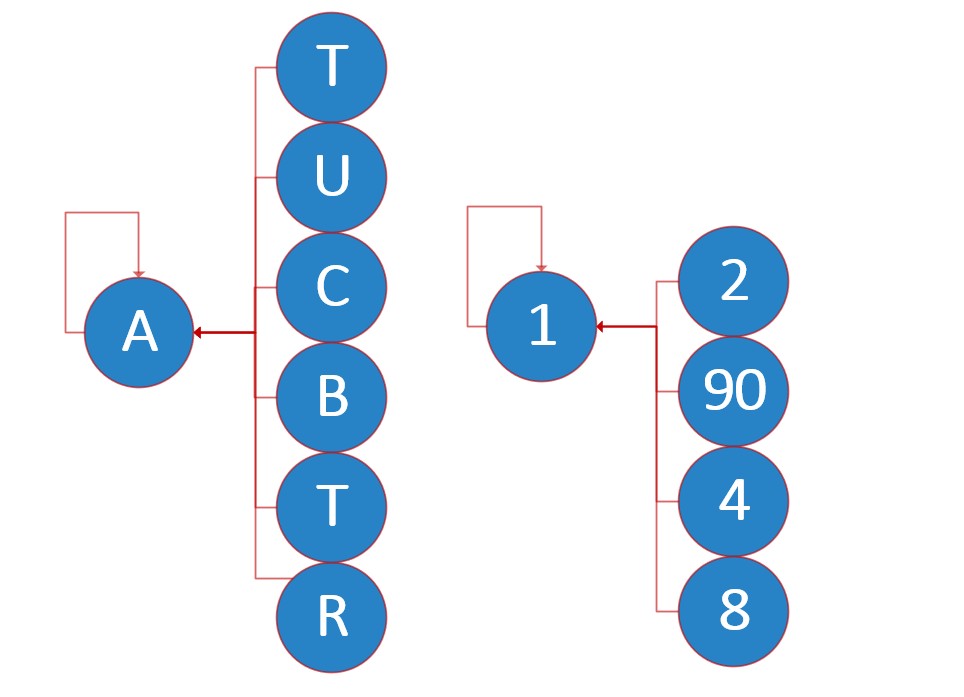
对于某一个集合一次路径压缩之后就变成了右图所示，不能找到是那两个集合合并了。
即使我们假设上次合并的是90和1，t=fa[90]=4 m=fa[4]=4，然后进行恢复，fa[4]=4然而并不能恢复，即使在恢复90，fa[90]=4之后，只是90和4被从树中摘除，然而我们看原图。
路径压缩是不行的

启发式合并

90和4之间还有个8我们还要记录8，如果中间还有很多元素，在每次查询和合并时都被压缩，我们就更难处理了，实际上经过路径压缩后的局面比我们想象的更加复杂。
所以我们不能使用路径压缩，那我们可以进行合并吗?我们知道普通合并是可以使用的，那么启发式合并或者按秩合并可以吗?
当然可以，这两种合并方式对于并查集来说是没有用影响的，无非就是a树挂在b节点上或者b树挂在节点a上面，对于并查集整体的恢复操作不会产生什么影响。

算法原理

并查集是一种树形的数据结构，它主要用于处理一些不相交集合的合并及查询问题。可撤销并查集的基本原理与并查集相似，但增加了一个撤销操作，我们需要做的就是对这一操作进行维护。
为了提高效率，我们采用启发式合并的优化方法。在可撤销并查集中，我们不使用路径压缩因为这样会破坏树形结构，导致在撤销操作时无法准确找到原始的父节点。在合并操作中，由于不使用路径压缩，查询的复杂度为$O(d)$，其中d为树的深度。为了降低树的深度，我们采用了启发式合并(或按秩合并)的方法。

那么我们可以给可撤销并查集的算法原理:

1. 查找
   由于支持撤销操作，那么肯定不能路径压缩，否则会破坏树形结构，反悔时无法找到原本的父节点。
2. 合并
   既然不能路径压缩，那么查询的复杂度就是0(a)的(d为深度)，所以我们要尽可能地减少树的深度，于是用到了一种合并方法–启发式合并(或按秩合并)启发式合并:
   维护每个集合的大小，合并时将小的集合合并到大的集合。
   时间复杂度:合并0(1)，查找0(logn)。
3. 撤销
   用栈来记录每次合并的操作，然后进行对fa，size等变量的维护即可

代码实现

1.定义所需变量

int n, q;
int fa[20000005], sz[2000005];

struct UndoObject
{
	int pos, val;
	UndoObject(int p, int v)
	{
		pos = p;
		val = v;
	}
};

stack<UndoObject> undo_sz, undo_fa;

用一个stack，先入后出，每次的操作往里放，先进去的会被晚撤销，撤销的一定是最近的这一步
undo_sz，记录树高
undo_fa，记录它的父亲是谁

声明了一些全局变量和数据结构，用于维护并查集的状态和实现撤销操作:
·n，q;:定义了两个全局变量n和q，分别表示数量和操作次数。fa[20000005]，siz[20000005];:定义了两个数组，fa 用于表示所属的集合的父节点,sz 用于表示每个集合的大小。
Undo0bject:定义了一个结构体(类) Undo0bject，用于存储撤销操作的详细信息。每个Undo0bject对象包含两个成员变量pos和val，分别表示位置和值。
undo_sz，undo fa;:定义了两个Undo0bject堆栈，undo sz 用于记录每次连接操作的集合大小和父节点信息，undo fa用于记录每次连接操作的父节点信息。
这些全局变量和数据结构主要用于在并查集的基础上实现了撤销操作。通过堆栈undo_sz和undo fa 记录每次连接操作的详细信息，程序可以在需要时撤销最近的操作，恢复到之前的状态。

2.初始化

void init(int n)
{
	for (int i = 1; i <= n; i ++)
		fa[i] = i, sz[i] = 1;  //一棵点，就是自己
	while (!undo_sz.empty())
		undo_sz.pop();  //清除之前的栈的内容
	while (!undo_fa.empty())
		undo_fa.pop();  //清除之前的栈的内容
}

static void init (int n)
{
	fa = new int[n + 1];  //要避过0
	sz = new int[n + 1];
	for (int i = 1; i <= n; i ++)
	{
		fa[i] = i;
		sz[i] = 1;
	}
	undo_sz = new Stack<>();
	undo_fa = new Stack<>();
}

初始化函数 init，用于在开始一个新的测试用例时，清空之前的状态信息，确保并査集处于初始状态。
该函数执行了以下操作:

• 初始化 fa 和 siz 数组:使用循环将每个初始化为独立的集合，即每个的父节点是自己，每个集合的大小为 1。
• 清空 undosz和 undo fa 栈:使用 while 循环，对两个堆栈undo sz 和 undo fa 分别调用 pop 操作，将之前的栈内容清空。
  当开始一个新的测试用例时，调用 init函数可以确保之前的状态信息不会对当前测试用例产生干扰。
  这对于在一个程序中多次执行并查集操作，每次都需要一个干净的状态时是非常有用的。

3.查询代码

int find (int x)
{
	if (x == fa[x])
		return x;
	return find(fa[x]);
}

并查集中的查找函数。并查集是一种数据结构，它能够高效地进行合并和查找操作。这个查找函数的作用是找到给定元素所在的集合的根节点。
int find(int x):定义一个函数find，它接受一个整数参数x，表示要查找的元素
if(x==fa[x])return x;: 如果x的父节点就是自己，说明x就是它所在的集合的根节点，直接返回x。
return find(fa[x]);:否则，递归地査找x的父节点的根节点，即调用find函数。将fa[x]作为参数传递给find函数，因为fa[x]是x的父节点，它所在的集合的根节点就是x所在的集合的根节点的父节点

4.合并代码

static void merge(int u, int v)
{
	int x = find(u);
	int y = find(v);
	if(x == y)  //如果相同，就不合并了
		return;
	if(sz[x] < sz[y])
	{
		int temp =x;
		x = y;
		y= temp;
	}
	//把原来的值放进去
	undo_sz.push(new UndoObject(x,sz[x]));
	//存完以后，改掉
	sz[x] += sz[y];
	//把原来的值放进去
	undo_fa.push(new UndoObject(y, fa[y]));
	//存完以后，改掉
	fa[y]= x;
}

这是并查集中的合并(连接)操作的实现，用于将两个节点所属的集合合并成一个集合。函数merge的具体步骤如下:

1. 使用find函数找到节点u所属集合的根节点x和节点v所属集合的根节点 y。
   1. 如果x和y相等，说明节点u和节点v已经在同一个集合中，无需合并，直接返回。
   2. 如果 sz[x]< sz[y]，即集合 x的大小小于集合 y的大小，那么交换x和 y，确保较大的集合成为合并后的集合的根节点。
2. 记录合并前的状态信息，将x的大小siz[x]和y的父节点 fa[y]分别入栈 undo_sz 和undo fa.
3. 更新集合大小和父节点信息，将集合y合并到集合x中。
   这个合并操作不仅将两个集合合并，还通过栈undo_sz和 undo_fa 记录了合并前的状态信息，以便后续可能的撤销操作。这种记录状态的设计可以在撤销时还原到之前的状态，使得操作更加灵活。

5.撤销代码

void undo()
{
	fa[undo_fa.top().pos]=undo_fa.top().val;
	undo_fa.pop();
	siz[undo_sz.top().pos]=undo_sz.top().val;
	undo_sz.pop();
}

这是用于撤销最近一次连接操作的函数 undo的实现。该函数通过栈undo_ fa和undo_sz 中记录的信息，将最近一次连接操作的状态还原到连接之前的状态。具体步如下:

1. 从 undo_fa 栈中取出最近一次连接操作前的状态信息，包括位置 pos 和父节点的值 val。然后，将城市 pos 的父节点更新为val。
2. 从 undo_sz 栈中取出最近一次连接操作前的状态信息，包括集合的根节点位置pos 和集合的大小 val。然后，将集合 pos 的大小更新为 val。
3. 分别从 undo_fa 和 undo_sz 栈中弹出这些信息;确保下一次 undo 操作不会再次撤销同一次连接操作。
   这个函数实现了撤销操作，可以在需要的时候将并查集的状态回滚到之前的状态