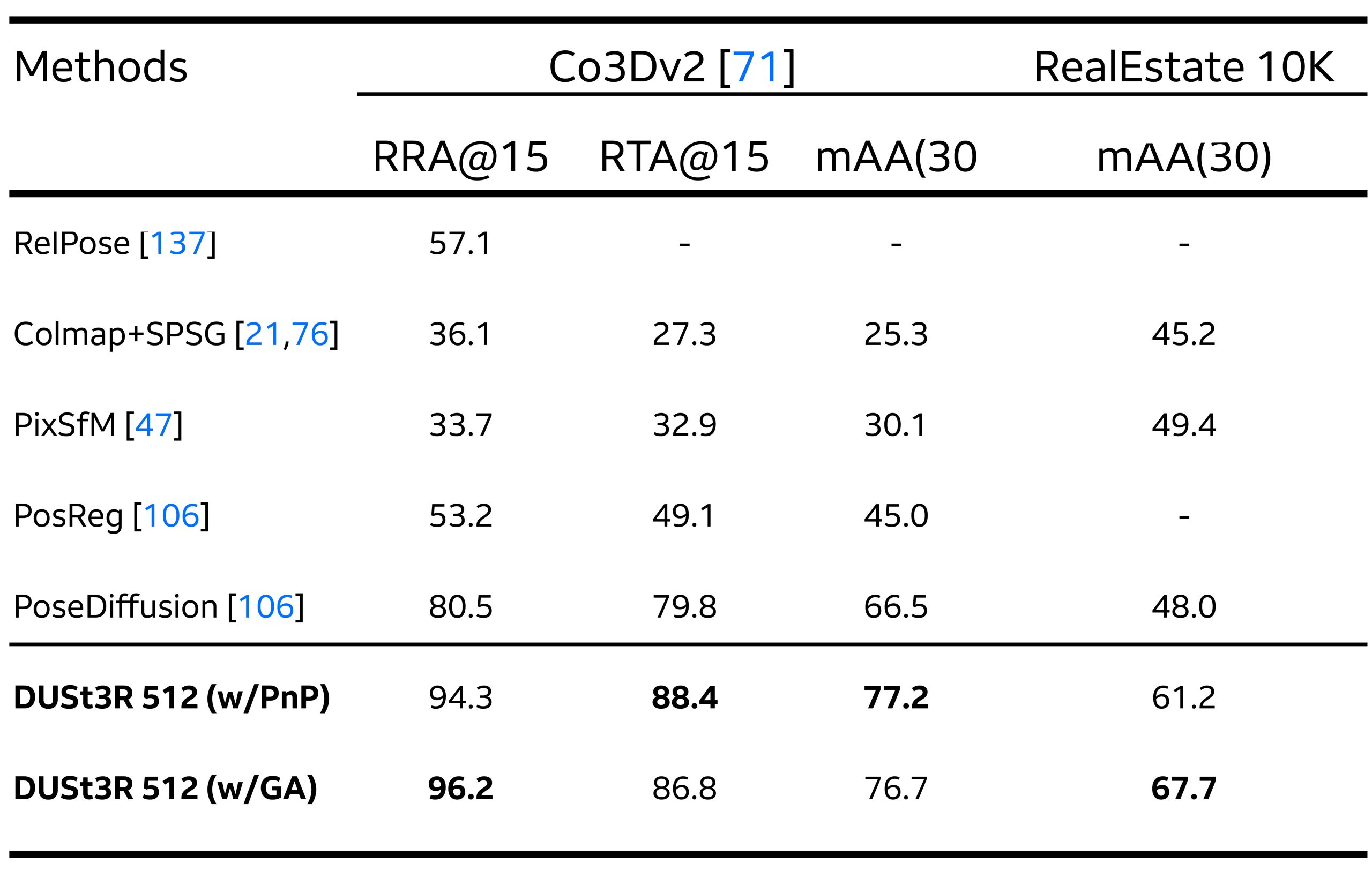
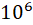题目1:题目 2335: 信息学奥赛一本通T1422-活动安排

设有n个活动的集合E={1,2,…,n}，其中每个活动都要求使用同一资源，如演讲会场等，而在同一时间内只有一个活动能使用这一资源。每个活动i都有一个要求使用该资源的起始时间si和一个结束时间fi,且si<fi。如果选择了活动i，则它在半开时间区间[si,fi)内占用资源。若区间[si,fi)与区间[sj,fj)不相交,则称活动i与活动j是相容的。也就是说，当si≥fj或sj≥fi时，活动i与活动j相容。选择出由相互兼容的活动组成的最大集合。

输入格式

第1行一个整数n(n≤1000)，接下来n行，每行两个整数si和fi。

输出格式

输出尽可能多的互相兼容的活动个数。

样例输入

4
1 3
4 6
2 5
1 7

样例输出

2

python代码

n=int(input())
t=[]
a=1#互相兼容的活动数量

for i in range(n):
    t.append(input().split())
for i in range(n):
    for j in range(2):
        t[i][j]=int(t[i][j])
t.sort(key=lambda x:x[0],reverse=True)#按照活动开始的时间进行降序排列
for i in range(n-1):
    if t[i][0]==t[i+1][0]:
        if t[i][1]>t[i+1][1]:
           t[i][1],t[i+1][1]=t[i+1][1],t[i][1]#左端点相同，将结束时间晚的放在后面
   
lastx=t[0][0]#最晚结束的活动的开始时间
for k in range(1,n):
    if t[k][1]<=lastx:#某一活动在它 开始之前结束
        lastx=t[k][0]
        a+=1
print(a)

知识点

1. 先把活动开始的时间进行降序排列，之后若左端点相同，将结束时间晚的放在后面，指针首先指向最晚结束的活动的开始时间，若是某一个活动的结束时间在它之前，那么这两个活动兼容
2. 另外一种思路：先把活动结束的时间进行升序排列，之后若左端点相同，将结束时间晚的放在后面，指针首先指向最早结束的活动的结束时间，若是某一个活动的开始时间在它之后，那么这两个活动兼容

题目2：P1002 [NOIP2002 普及组] 过河卒

棋盘上 A 点有一个过河卒，需要走到目标
B 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 C 点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示，
A 点 (0,0)、B 点 (n,m)，同样马的位置坐标是需要给出的。

输入格式

一行四个正整数，分别表示 B 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

样例输入

6 6 3 3

样例输出

6

python代码

x,y,n,m=map(int,input().split())
x+=1
y+=1
n+=1
m+=1#便于计算，索引值从1开始


ma=[[0]*25 for _ in range(25) ]#马的位置
step=[[0]*25 for _ in range(25)]#坐标

ma[n][m]=1
step[1][1]=1


ma[n-2][m-1]=1#马能到达的位置
ma[n-2][m+1]=1
ma[n+2][m-1]=1
ma[n+2][m+1]=1
ma[n-1][m-2]=1
ma[n-1][m+2]=1
ma[n+1][m-2]=1
ma[n+1][m+2]=1

for i in range(1,x+1):
    for j in range(1,y+1):
        if (i!=1 or j!=1) and(not ma[i][j]):
            step[i][j]=step[i-1][j]+step[i][j-1]
print(step[x][y])

知识点

1. 二维列表的建立方式：最初我以为ma=[[0]*5]*5来建立的，后来运行的时候一直报错，才知道这种方法会指向列，对某一值修改会对整列进行修改，那么正确的创建方式为：
2. ma=[[0]*5 for _ in range(5)]
3. 找到正常情况下的递推公式：step[i][j]=step[i-1][j]+step[i][j-1]（只能向右或向下）
4. 最后 把非正常情况的点 去除

题目3：

你的程序将由操作数序列 1,2,…,n 经过操作可能得到的输出序列的总数。

输入格式

输入文件只含一个整数 𝑛

输出格式

输出文件只有一行，即可能输出序列的总数目

样例输入

3

样例输出

5

python代码

n=int(input())
ans=1
for i in range(1,n+1):
    ans=ans*(4*i-2)//(i+1)
print(f'{ans:d}')

知识点

1. 卡特兰数
2. 进出栈序列：n 个元素进栈序列为：1，2，3，4，…，n，则有多少种出栈序列？

结论：
$$C_{{}_n}=C_{{}_{n-1}}\ast \frac{4\ast n-2}{n+1}$$

题目4:# [NOIP2001 普及组] 数的计算

题目描述

给出正整数 $n$，要求按如下方式构造数列：

1. 只有一个数字 $n$ 的数列是一个合法的数列。
2. 在一个合法的数列的末尾加入一个正整数，但是这个正整数不能超过该数列最后一项的一半，可以得到一个新的合法数列。

请你求出，一共有多少个合法的数列。两个合法数列 $a,b$ 不同当且仅当两数列长度不同或存在一个正整数 $i\le |a|$，使得 $a_i\ne b_i$。

输入格式

输入只有一行一个整数，表示 $n$。

输出格式

输出一行一个整数，表示合法的数列个数。

样例 #1

样例输入 #1

6

样例输出 #1

6

提示

样例 1 解释

满足条件的数列为：

• $6$
• $6,1$
• $6,2$
• $6,3$
• $6,2,1$
• $6,3,1$

数据规模与约定

对于全部的测试点，保证 $1\le n\le 10^3$。

python代码

def count(n):
    global ans
    for i in range(1,n+1):
        for j in range(1,int(i/2)+1):
            f[i]+=f[j]
        f[i]+=1
    
n=int(input())
ans=1#自身
f=[0]*1001
if n==1:
    print(ans)
else:
    count(n)
    print(f[n])

知识点

1. 先找规律,然后代码实现
2. f(1)=1,f(2)=2,f(3)=2
3. f(4)=f(1)+f(2)+1
4. f(5)=f(1)+f(2)+1
5. f(6)=f(1)+f(2)+f(3)+1
6. f(7)=f(1)+f(2)+f(3)+1

题目5：# 黑白棋子的移动

题目描述

有 $2n$ 个棋子排成一行，开始为位置白子全部在左边，黑子全部在右边，如下图为 $n=5$ 的情况：

移动棋子的规则是：每次必须同时移动相邻的两个棋子，颜色不限，可以左移也可以右移到空位上去，但不能调换两个棋子的左右位置。每次移动必须跳过若干个棋子（不能平移），要求最后能移成黑白相间的一行棋子。如 $n=5$ 时，成为：

任务：编程打印出移动过程。

输入格式

一个整数 $n$。

输出格式

若干行，表示初始状态和每次移动的状态，用 $\text{o}$ 表示白子，$\text{*}$ 表示黑子，$\text{-}$ 表示空行。

样例 #1

样例输入 #1

7

样例输出 #1

ooooooo*******--
oooooo--******o*
oooooo******--o*
ooooo--*****o*o*
ooooo*****--o*o*
oooo--****o*o*o*
oooo****--o*o*o*
ooo--***o*o*o*o*
ooo*o**--*o*o*o*
o--*o**oo*o*o*o*
o*o*o*--o*o*o*o*
--o*o*o*o*o*o*o*

python代码

def printx():#打印单元
    for i in range(2*n+2):
        print(c[i],end='')
    print()
    
def move(n):
    if n==4:#n==4时，已经为最小问题，需要列举
        c[3],c[8]=c[8],c[3]
        c[4],c[9]=c[9],c[4]        
        printx()#打印第一步
        c[3],c[7]=c[7],c[3]
        c[4],c[8]=c[8],c[4]
        printx()#打印第二步
        c[1],c[7]=c[7],c[1]
        c[2],c[8]=c[8],c[2]
        printx()#打印第三步
        c[1],c[6]=c[6],c[1]
        c[2],c[7]=c[7],c[2]
        printx()#打印第四步
        c[0],c[6]=c[6],c[0]
        c[1],c[7]=c[7],c[1]
        printx()#打印第五步
    else:
        c[n-1],c[2*n]=c[2*n],c[n-1]
        c[n],c[2*n+1]=c[2*n+1],c[n]
        printx()
        c[n-1],c[2*n-2]=c[2*n-2],c[n-1]
        c[n],c[2*n-1]=c[2*n-1],c[n]
        printx()
        move(n-1)


    

n=int(input())
c=[]#存放元素
for i in range(n):
    print('o',end='')
    c.append('o')


for j in range(n,2*n):
    print('*',end='')
    c.append('*')
c.append('-')
c.append('-')#一共2n+2个值，索引到c[2n+1]
print('--')
move(n)

知识点

1. 首先找规律，之后从最小的单元开始，即n=4，会发现n=5移动2步后就会变为n=4的问题，依次形成递归的思路
2. 注意每一步调用printx()函数，对于未完全输出一行数据，end='',一行输出完毕，利用print()换行

题目6：# [NOIP1998 普及组] 幂次方

题目描述

任何一个正整数都可以用 $2$ 的幂次方表示。例如 $137=2⁷⁺²3+2^0 $。

同时约定次方用括号来表示，即 $a^b$ 可表示为 $a(b)$。

由此可知，$137$ 可表示为 $2(7)+2(3)+2(0)$

进一步：

$7=2^2+2+2^0$ ( $2^1$ 用 $2$ 表示)，并且 $3=2+2^0$。

所以最后 $137$ 可表示为 $2(2(2)+2+2(0))+2(2+2(0))+2(0)$。

又如 $1315=2^{10}+2^8+2^5+2+1$

所以 $1315$ 最后可表示为 $2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)$。

输入格式

一行一个正整数 $n$。

输出格式

符合约定的 $n$ 的 $0,2$ 表示（在表示中不能有空格）。

样例 #1

样例输入 #1

1315

样例输出 #1

2(2(2+2(0))+2)+2(2(2+2(0)))+2(2(2)+2(0))+2+2(0)

提示

【数据范围】

对于 $100\%$ 的数据，$1\le n\le 2\times {10}^4$。

python代码

def culi(n):
    m=0#记录幂
    if n==1:#最小问题
        print('2(0)',end='')
    elif n==2:
        print('2',end='')
    elif n>=3:
        while n>=a[m+1]:#找到最大的幂
            m+=1
        #print(m)
        n-=a[m]
        print('2',end='')
        if m>=2:
            print('(',end='')
            culi(m)
            print(')',end='')

            
        if n!=0:#子问题
            print('+',end='')
            culi(n)

n=int(input())
a=[]
for i in range(16):
    a.append(pow(2,i))
culi(n)

知识点

1. 数学分治+递归的思想，当n>=3,拆分成n=1或n=2的问题
2. 由于最大的数值不是很大（2^15），所以利用查表确定最大的索引值，之后进行两次递归。