我们今天继续来随机看5道AMC10真题，以及详细解析，这些题目来自1250道完整的官方历年AMC10真题库。通过系统研究和吃透AMC10的历年真题，参加AMC10的竞赛就能拿到好名次。即使不参加AMC10竞赛，掌握了这些知识和解题思路后初中和高中数学会学得比较轻松、游刃有余。

孩子学有余力的情况下，参加一下这个比赛也是激发兴趣和好胜心的一种方法，以赛促学。也是孩子宝贵的一种学习经历和见识。

为帮助大家，我整理了2000-2023年的全部AMC10的A卷和B卷的真题共1250题，并且独家制作了多种在线练习，利用碎片化时间，一年足以通过自学在2024年AMC10竞赛中取得好成绩。

好消息：2000-2023年的AMC10AB卷真题限时免费赠送，免费体验独家设计的在线练习集，欢迎了解和获取。

2000-2023年AMC10真题练习和解析：2022年第19题

这道题的考点是组合，答案为C。

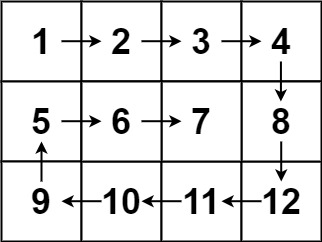
根据题意，除了中间的格子，初始情况下其他格子需要满足下列条件：

①每个灰色填充的格子的周围最多只有1个是灰色的。

②其他空白格子周围最多只有2个是灰色的。

接下来我们对初始情况下中间格子是空的还是灰色的进行分类讨论：

2000-2023年AMC10真题练习和解析：2014年第4题

这道题的考点是代数（列方程解应用题）。

我们假设香蕉是1元一根，玛芬是x元一个，那么根据题意列出方程：2x+16=2(4x+3),解得x=5/3，所以答案选B。

2000-2023年AMC10真题练习和解析：2012年第20题

这道题考点为代数，答案为A，解析过程如下：

提醒：算出答案以后，求这个数各个位上的数字之和还偶尔会考到，需注意审题，否则虽然算出了整数，但找不到答案会怀疑自己做错了。

2000-2023年AMC10真题练习和解析：2009年第21题

这道题的考点是等比数列和数论的余数。

我们先求出等比数列前2010项之和，再求除以8的余数即可。答案为D，计算过程如下：

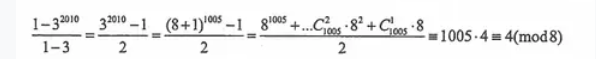
2000-2023年AMC10真题练习和解析：2001年第20题

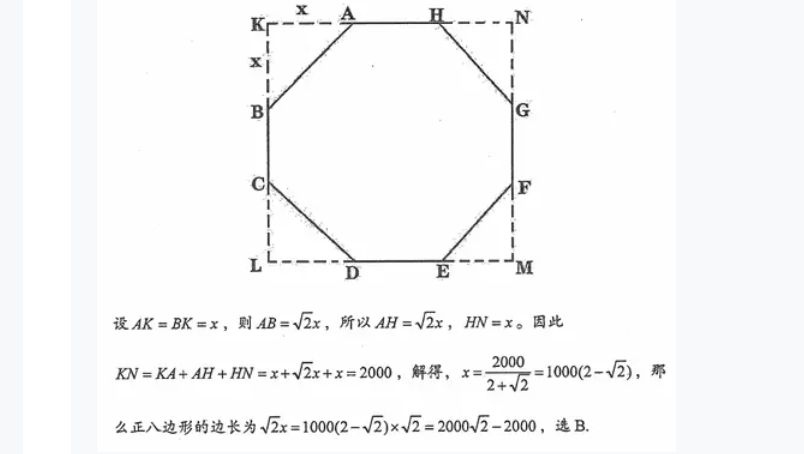
这道题目的考点是平面几何，正八边形的特点。根据题意，可以知道，正八边形的边长即为等腰直角三角形的斜边，等于√2的等腰直角三角形的直角边。画出图形计算即可，答案为B，解析过程如下：

---

六分成长针对AMC10备考资源，欢迎了解更多

上述六分成长独家制作的在线练习题，符合学习和认知心理学，来源于完整的历年AMC8和AMC10真题，并且会持续更新。AMC8和AMC10备考可用，反复练习，也有利于小学、初中数学能力提升。

欢迎联系我免费获得AMC10历年真题1250道，并免费体验独家设计的在线练习集。