时序分解 | Matlab实现GWO-CEEMDAN基于灰狼算法优化CEEMDAN时间序列信号分解
目录
- 时序分解 | Matlab实现GWO-CEEMDAN基于灰狼算法优化CEEMDAN时间序列信号分解
- 效果一览
- 基本介绍
- 程序设计
- 参考资料
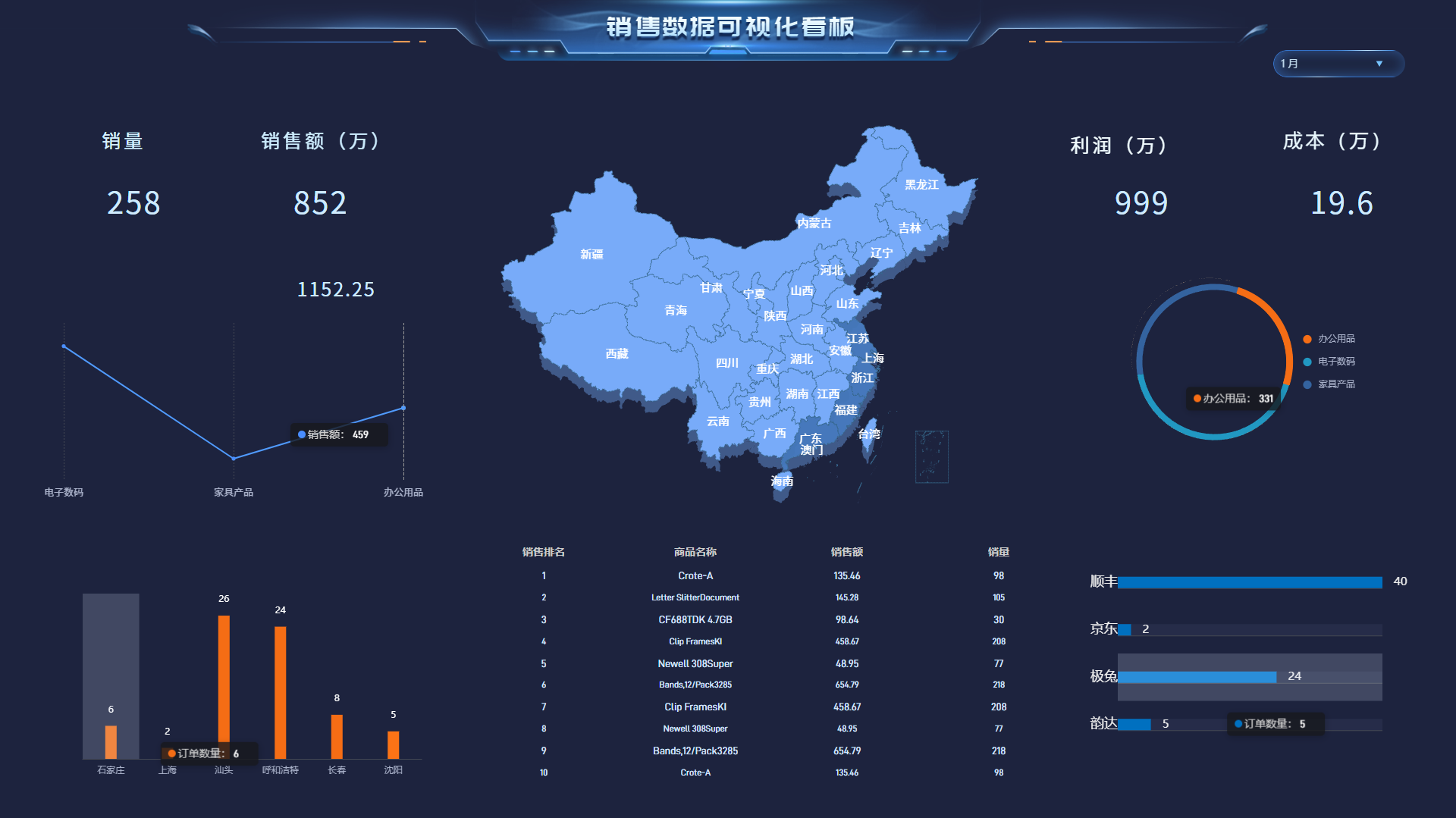
效果一览





基本介绍
1.CEEMDAN方法的分解效果取决于白噪声幅值权重(Nstd)和噪声添加次数(NE),因此,采用智能优化算法对这2个参数进行优化,适应度函数包括包络熵、样本熵、信息熵、排列熵,可随时切换(Matlab完整源码和数据)
2.直接替换Excel数据即可用,注释清晰,适合新手小白
3.附赠时间序列测试数据,可直接运行main一键出图
程序设计
- 完整源码和数据获取方式私信博主回复:Matlab实现GWO-CEEMDAN基于灰狼算法优化CEEMDAN时间序列信号分解。
%% 以最小包络熵、最小样本熵、最小信息熵、最小排列熵为目标函数(任选其一),采用优化CEEMDAN,求取CEEMDAN最佳的两个参数
clear
clc
close all
xz = 1; %xz=1 or 2, 选择1,以最小包络熵为适应度函数,选择2,以最小样本熵为适应度函数,选择3,以最小信息熵为适应度函数,选择4,以最小排列熵为适应度函数
if xz == 1
fobj=@EnvelopeEntropyCost; %最小包络熵
elseif xz == 2
fobj=@SampleEntropyCost; %最小样本熵
elseif xz == 3
fobj=@infoEntropyCost; %最小信息熵
elseif xz == 4
fobj=@PermutationEntropyCost; %最小排列熵
end
%% 选取数据
da = xlsread('测试数据.xlsx','B:B'); %这里选取测试数据,B代表Excel中的第B列,注意这里替换为自己的数据即可,数据形式为n行*1列,列数必须为1。
plot(da);
title('原始信号')
set(gcf,'color','w')
%% 设置参数
lb = [0.15 50]; % 噪声幅值权重的优化范围设置为[0.15,0.6],噪声添加次数的优化范围为[50,600]
ub = [0.6 600];
dim = 2; % 优化变量数目
Max_iter=20; % 最大迭代数目
SearchAgents_no=10; % 种群规模
%% 调用NGO函数
disp('代码运行时间较长,请耐心等待!')
[fMin , bestX, Convergence_curve ] = GWO(SearchAgents_no,Max_iter,lb,ub,dim,fobj,da);
%% 画适应度函数曲线图,并输出最佳参数
figure
plot(Convergence_curve,'linewidth',1);
title('迭代曲线图')
xlabel('迭代次数');
ylabel('适应度值');
legend('GWO优化CEEMDAN')
set(gcf,'color','w')
display(['GWO最佳位置为: ', num2str(bestX)]); %输出最佳位置
display(['GWO最佳适应度值为 : ', num2str(fMin)]); %输出最佳适应度值
%% CEEMDAN分解图
X = da;
Nstd = bestX(1);
NR = fix(bestX(2));
MaxIter = 10;
[anmodes,its]=ceemdan(X,Nstd,NR,MaxIter);
plotimf(anmodes,size(anmodes,1),'r',' CEEMDAN分解结果'); %画图
xlswrite('GWO-CEEMDAN分解结果.xlsx',anmodes);
%% 频谱图
fs=1;
N=400;
u=anmodes;
figure('Name','频谱图','Color',[1 1 1])
for i=1:size(u,1)
subplot(size(u,1) ,1,i)
[cc,y_f]=plot_fft(u(i,:),fs,1);
plot(y_f,cc,'b','LineWIdth',1);
ylabel(['IMF',num2str(i)]);
end
参考资料
[1] https://blog.csdn.net/kjm13182345320/article/details/129215161
[2] https://blog.csdn.net/kjm13182345320/article/details/128105718## 标题