力扣日记：【贪心算法篇】55. 跳跃游戏

日期：2024.3.19
参考：代码随想录、力扣

55. 跳跃游戏

题目描述

难度：中等

给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：

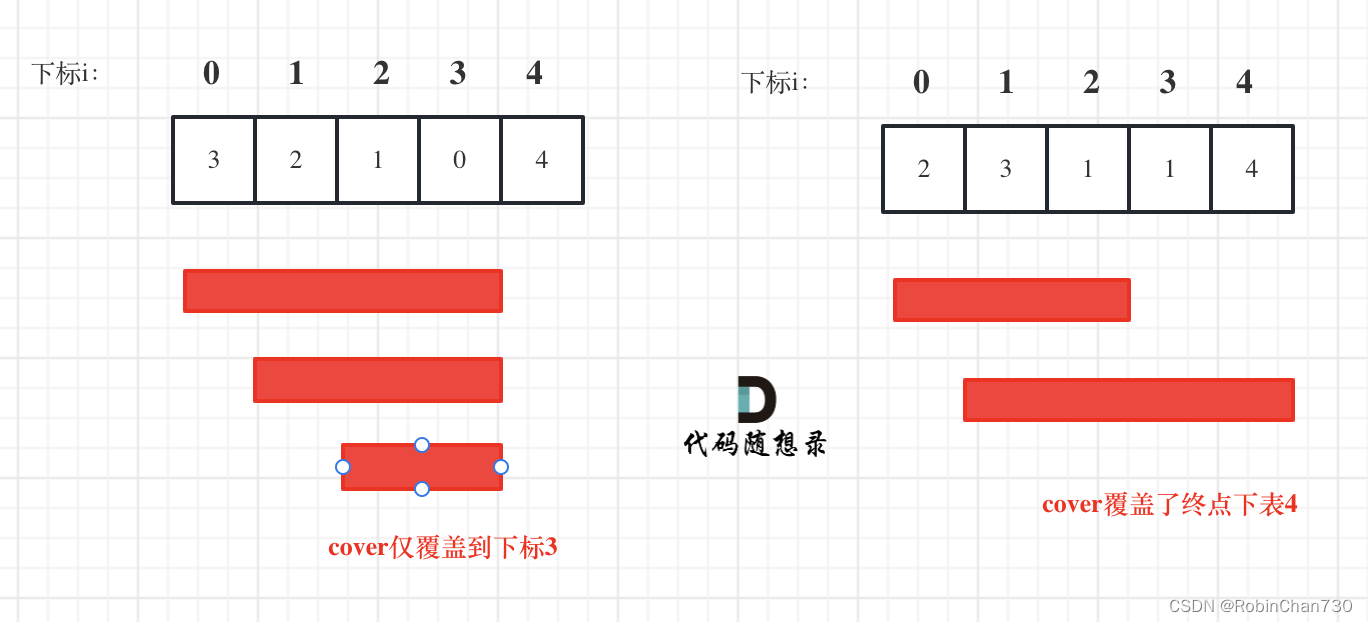
输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

提示：

• 1 <= nums.length <= 10^4
• 0 <= nums[i] <= 10^5

题解

class Solution {
public:
#define SOLUTION 2
#if SOLUTION == 1   /*回溯法，超出时间限制*/
    bool canJump(vector<int>& nums) {
        return backtracking(nums, 0);
    }
    bool backtracking(vector<int>& nums, int startindex) {
        // 终止条件：如果已经到达最后一个下标
        if (startindex >= nums.size() - 1) {
            return true;
        }
        // for 循环
        // 从大到小横向遍历这个元素值（选择可以跳跃的长度）
        for (int i = nums[startindex]; i > 0; i--) {
            startindex += i;    // 跳到下一个位置
            if (backtracking(nums, startindex)) return true;
            // 如果当前跳跃步数无法到最后一个坐标，则回溯
            startindex -= i;
        }
        return false;
    }
#elif SOLUTION == 2
    bool canJump(vector<int>& nums) {
        // 看最大覆盖范围！但每次只移动一个长度(关键！！！)，并不断更新最大覆盖范围（最大可到达的下标）
        // 局部最优：获取每个位置当前可到达的最大下标
        // 全局最优：遍历可到达的全部元素，找到其中最大的可到达下标即为总的最大下标
        int curMaxIndex = 0;
        for (int i = 0; i <= curMaxIndex; i++) {    // 最大只能到curMaxIndex（不断更新）
            if (i + nums[i] > curMaxIndex) {    // 如果新的当前位置可到达的最大长度 比 curMaxIndex 大，则更新
                curMaxIndex = i + nums[i];
            }
            if (curMaxIndex >= nums.size() - 1) {   // 如果已能到达最后一个下标，则返回true
                return true;
            }
        }
        return false;
    }
#endif
};

复杂度

贪心算法：

• 时间复杂度：O(n)
• 空间复杂度：O(1)

思路总结

• 一开始尝试用回溯算法，虽然思路是正确的，但回溯法相当于穷举，结果超出时间范围了
• 参考代码随想录的思路：

  • 看最大覆盖范围！注意每次只移动一个长度(关键！！！)，并不断更新最大覆盖范围（即最大可到达的下标）

    • 这样的话，就可以不管究竟在每个位置要跳几步，只要知道在覆盖范围内的每个位置能到达的最大下标即可（能覆盖到最大下标即成功）。
    • 

  • 局部最优：获取每个位置当前可到达的最大下标

  • 全局最优：遍历覆盖范围内即可到达的全部元素，找到其中最大的可到达下标即为总的最大下标