【滑动窗口、矩阵】算法例题

news2025/11/1 2:28:11

目录

 三、滑动窗口

30. 长度最小的子数组 ②

31. 无重复字符的最长子串 ②

32. 串联所有单词的子串 ③

33. 最小覆盖子串 ③

四、矩阵

34. 有效的数独 ②

35. 螺旋矩阵 ②

36. 旋转图像 ②

37. 矩阵置零 ②

38. 生命游戏 ②

 三、滑动窗口

30. 长度最小的子数组 ②

 给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3]
 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

  • 1 <= target <= 109
  • 1 <= nums.length <= 105
  • 1 <= nums[i] <= 105

力扣题解：. - 力扣（LeetCode）

方法1：时间超时（通过15/18）

    public int minSubArrayLen(int target, int[] nums) {
        int min = nums.length + 1;
        for (int i = 0; i < nums.length; i++) {
            int sum = 0;
            int left = i;
            sum += nums[left];
            int right = i + 1;
            while (right < nums.length && sum < target){
                sum += nums[right];
                right++;
            }
            if (sum >= target && min > right - left){
                min = right - left;
            }
        }
        return min == nums.length + 1? 0 : min;
    }

方法2：(0ms)

    public int minSubArrayLen(int target, int[] nums) {
        int l = 0, r = 0;
        int n = nums.length;
        int sum = 0;

        while(r < n && sum < target)
            sum += nums[r++];

        if(r == n)
            if (sum < target)
                return 0;
            else{
                while(sum > target)
                    sum -= nums[l++];
            }

        while(r < n){
            if(sum < target) sum += nums[r++];
            sum -= nums[l++];
        }
        if(sum < target) return r-l+1;
        return r -l;
    }

方法3：

    public int minSubArrayLen(int target, int[] nums) {
        int lo = 0, hi = 0, sum = 0, min = Integer.MAX_VALUE;
        while (hi < nums.length) {
            sum += nums[hi++];
            while (sum >= target) {
                min = Math.min(min, hi - lo);
                sum -= nums[lo++];
            }
        }
        return min == Integer.MAX_VALUE ? 0 : min;
    }

 方法4：（2ms）

    public int minSubArrayLen(int target, int[] nums) {
         int left = 0;
        int res = Integer.MAX_VALUE;
        int add = 0;
         for (int right = 0; right < nums.length; right++) {
            add += nums[right];
            while (add >= target) {
                res = Math.min(res, right - left + 1);
                add -= nums[left];
                ++left;
            }
        }
        return res > nums.length ? 0 : res;
    }

31. 无重复字符的最长子串 ②

 给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

提示：

  • 0 <= s.length <= 5 * 104
  • s 由英文字母、数字、符号和空格组成

方法1：（7ms）

    public static int lengthOfLongestSubstring(String s) {
        TreeSet<Integer> set = new TreeSet<>();
        if (s.length() == 0){
            return 0;
        }else if (s.length() == 1){
            return 1;
        }else {
            int left = 0;
            int right = 1;
            while (right < s.length()){
                String substring = s.substring(left, right);
                if (substring.contains(s.charAt(right) + "")){
                    set.add(right - left);
                    left = s.indexOf(s.charAt(right), left) + 1;
                }else {
                    if (right == s.length() - 1) {
                        set.add(right - left + 1);
                        break;
                    }
                }
                right++;
            }
            return set.last();
        }
    }

方法2：（滑动窗口  5ms）

    public int lengthOfLongestSubstring(String s) {
        if (s.length()==0) return 0;
        HashMap<Character, Integer> map = new HashMap<Character, Integer>();
        int max = 0;
        int left = 0;
        for(int i = 0; i < s.length(); i ++){
            if(map.containsKey(s.charAt(i))){
                left = Math.max(left,map.get(s.charAt(i)) + 1);
            }
            map.put(s.charAt(i),i);
            max = Math.max(max,i-left+1);
        }
        return max;
        
    }

作者：powcai
链接：https://leetcode.cn/problems/longest-substring-without-repeating-characters/solutions/3982/hua-dong-chuang-kou-by-powcai/

32. 串联所有单词的子串 ③

33. 最小覆盖子串 ③

四、矩阵

34. 有效的数独 ②

 请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

  1. 数字 1-9 在每一行只能出现一次。
  2. 数字 1-9 在每一列只能出现一次。
  3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

注意：

  • 一个有效的数独（部分已被填充）不一定是可解的。
  • 只需要根据以上规则，验证已经填入的数字是否有效即可。
  • 空白格用 '.' 表示。

示例 1：

输入：board = 
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：true

示例 2：

输入：board = 
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：false
解释：除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

提示：

  • board.length == 9
  • board[i].length == 9
  • board[i][j] 是一位数字（1-9）或者 '.'

方法1：

    public static boolean isValidSudoku(char[][] board) {
        String[] rows = new String[9];
        String[] columns = new String[9];
        String[] areas = new String[9];
        for (int i = 0; i < 9; i++) {
            if (rows[i] == null){
                rows[i] = "a";
            }

            for (int j = 0; j < 9; j++) {
                if (columns[j] == null){
                    columns[j] = "a";
                }
                if (rows[i].contains(board[i][j] + "")){
                    return false;
                }else if (board[i][j] != '.' && !rows[i].contains(board[i][j] + "")){
                    rows[i] += board[i][j];
                }
                if (columns[j].contains(board[i][j] + "")){
                    return false;
                }else if (board[i][j] != '.' && !columns[j].contains(board[i][j] + "")){
                    columns[j] += board[i][j];
                }
                int row = i / 3; // 0 1 2
                int column = j / 3; //0 1 2
                int area = row * 3 + column;
                if (areas[area] == null){
                    areas[area] = "a";
                }
                if (areas[area].contains(board[i][j] + "")){
                    return false;
                }else  if (board[i][j] != '.' && !areas[area].contains(board[i][j] + "")){
                    areas[area] += board[i][j];
                }
            }
        }
        return true;
    }

方法2：（0ms）

    public boolean isValidSudoku(char[][] board) {
        short[] rows = new short[9];
        short[] cols = new short[9];
        short[] squares = new short[9];
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                if (board[i][j] != '.') {
                    short value = (short)(1 << (board[i][j] - '0'));
                    int boxNum = i / 3 * 3 + j / 3;
                    if ((rows[i] & value) != 0 || (cols[j] & value) != 0 || (squares[boxNum] & value) != 0) {
                        return false;
                    }
                    rows[i] |= value;
                    cols[j] |= value;
                    squares[boxNum] |= value;
                }
            }
        }
        return true;
    }

方法3：（1ms）

    public boolean isValidSudoku(char[][] board) {
        int[] rows = new int[9];
        int[] cols = new int[9];
        int[] subboxes = new int[9];
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                char c = board[i][j];
                if (c != '.') {
                    int x = (1 << (c - '1'));
                    if ((rows[i] & x) != 0) {
                        return false;
                    } else {
                        rows[i] |= x;
                    }
                    if ((cols[j] & x) != 0) {
                        return false;
                    } else {
                        cols[j] |= x;
                    }
                    if ((subboxes[i / 3 * 3 + j / 3] & x) != 0) {
                        return false;
                    } else {
                        subboxes[i / 3 * 3 + j / 3] |= x;
                    }
                }
            }
        }
        return true;
    }

方法4：（2ms）

    public boolean isValidSudoku(char[][] board) {            
        int[][] row = new int[9][9]; // 行
        int[][] columns = new int[9][9]; // 列
        int[][][] a = new int[3][3][9];
        for (int i = 0; i < 9; i++) {
            Set<Character> set = new HashSet<>();
            for (int j = 0; j < 9; j++) {
                char c = board[i][j];
                if (c != '.') {
                    row[i][c - 49]++;
                    columns[j][c - 49]++;
                    a[i / 3][j / 3][c - 49]++;
                    if (row[i][c - 49] > 1 || columns[j][c - 49] > 1 || a[i / 3][j / 3][c - 49] > 1) {
                        return false;
                    }
                }

            }
        }
        return true;
    }

35. 螺旋矩阵 ②

 给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

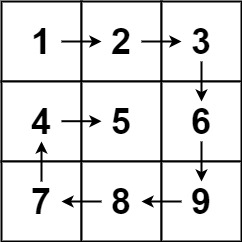
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 10
  • -100 <= matrix[i][j] <= 100

方法1：（0ms）

    public static List<Integer> spiralOrder(int[][] matrix) {
        int[][] path = new int[matrix.length][matrix[0].length];
        int step = 0;
        ArrayList<Integer> list = new ArrayList<>();
        int row = 0;
        int col = 0;
        int direct = 0;
        while (step < matrix.length * matrix[0].length){
            list.add(matrix[row][col]);
            path[row][col] = 1;
            if (direct == 0){
                col++;
                if (col == matrix[0].length || path[row][col] == 1){
                    direct = 1;
                    col--;
                    row++;
                }
            }else if (direct == 1){
                row++;
                if (row == matrix.length || path[row][col] == 1){
                    direct = 2;
                    row--;
                    col--;
                }
            }else if (direct == 2){
                col--;
                if (col == -1 || path[row][col] == 1){
                    direct = 3;
                    col++;
                    row--;
                }
            }else {
                row--;
                if (row == 0 || path[row][col] == 1){
                    direct = 0;
                    row++;
                    col++;
                }
            }
            step++;
        }
        return list;
    }

方法2：（0ms）

   public List<Integer> spiralOrder(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        List<Integer> res = new ArrayList<>();
        int u = 0, d = m - 1, l = 0, r = n - 1;
        while (true) {
            for (int i = l; i <= r; i ++) res.add(matrix[u][i]);
            if (++u > d) break;
            for (int i = u; i <= d; i ++) res.add(matrix[i][r]);
            if (--r < l) break;
            for (int i = r; i >= l; i --) res.add(matrix[d][i]);
            if (--d < u) break;
            for (int i = d; i  >= u; i --) res.add(matrix[i][l]);
            if (++l > r) break;
        }
        return res; 
    }

36. 旋转图像 ②

 给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

  • n == matrix.length == matrix[i].length
  • 1 <= n <= 20
  • -1000 <= matrix[i][j] <= 1000

方法1：（0ms）

    public static void rotate(int[][] matrix) {
        int n = matrix.length;
        int row = 0;
        int col = n - 1;
        int index = 0;
        while (row < col){
            while (row + index < col) {
                int leftUp = matrix[row][row + index];
                int rightUp = matrix[row + index][col];
                int rightDown = matrix[col][col - index];
                int leftDown = matrix[col - index][row];
                matrix[row][row + index] = leftDown;
                matrix[row + index][col] = leftUp;
                matrix[col][col - index] = rightUp;
                matrix[col - index][row] = rightDown;
                index++;
            }
            index = 0;
            row++;
            col--;
        }

    }

37. 矩阵置零 ②

 给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

示例 1：

输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

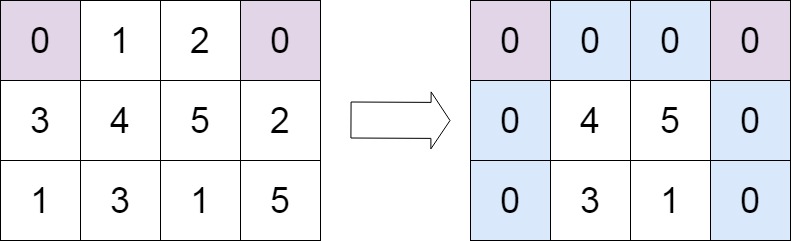
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

  • m == matrix.length
  • n == matrix[0].length
  • 1 <= m, n <= 200
  • -231 <= matrix[i][j] <= 231 - 1

进阶：

  • 一个直观的解决方案是使用  O(mn) 的额外空间，但这并不是一个好的解决方案。
  • 一个简单的改进方案是使用 O(m + n) 的额外空间，但这仍然不是最好的解决方案。
  • 你能想出一个仅使用常量空间的解决方案吗？

方法1：

    public void setZeroes(int[][] matrix) {
        TreeSet<Integer> rowSet = new TreeSet<>();
        TreeSet<Integer> columnSet = new TreeSet<>();
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                if (matrix[i][j] == 0){
                    rowSet.add(i);
                    columnSet.add(j);
                }
            }
        }
        for (int i = 0; i < matrix.length; i++) {
            if (rowSet.contains(i)){
                Arrays.fill(matrix[i], 0);
            }
        }
        for (int i = 0; i < matrix[0].length; i++) {
            if (columnSet.contains(i)){
                for (int j = 0; j < matrix.length; j++) {
                    matrix[j][i] = 0;
                }
            }
        }
    }

方法2：

    public void setZeroes(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        // 统计行列是否需要置为0 空间复杂度 O(m+n)
        boolean[] zeroRow = new boolean[m];
        boolean[] zeroCol = new boolean[n];
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(matrix[i][j] == 0){
                    zeroRow[i] = true;
                    zeroCol[j] = true;
                }
            }
        }

        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(zeroRow[i] || zeroCol[j]) {
                    matrix[i][j] = 0;
                }
            }
        }
    }

38. 生命游戏 ②

 根据 百度百科 ， 生命游戏 ，简称为 生命 ，是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。

给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态： 1 即为 活细胞 （live），或 0 即为 死细胞 （dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：

  1. 如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；
  2. 如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；
  3. 如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；
  4. 如果死细胞周围正好有三个活细胞，则该位置死细胞复活；

下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态，返回下一个状态。

示例 1：

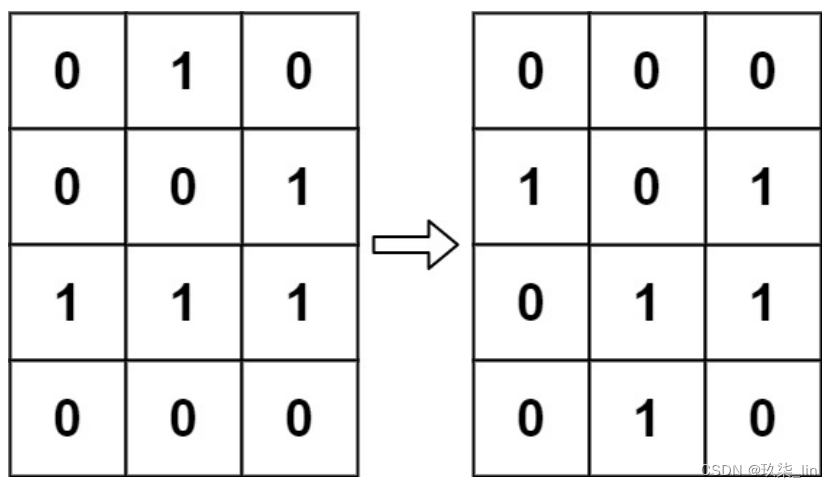
输入：board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
输出：[[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

示例 2：

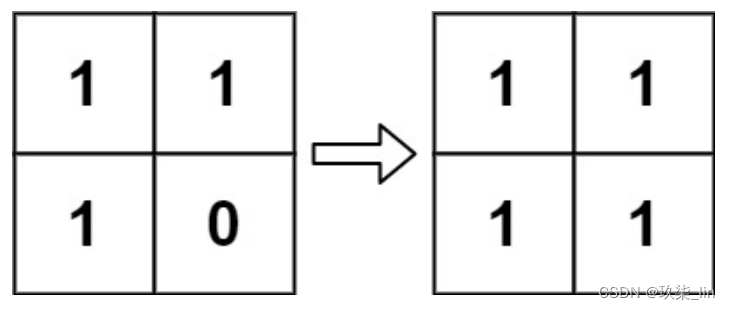
输入：board = [[1,1],[1,0]]
输出：[[1,1],[1,1]]

提示：

  • m == board.length
  • n == board[i].length
  • 1 <= m, n <= 25
  • board[i][j] 为 0 或 1

进阶：

  • 你可以使用原地算法解决本题吗？请注意，面板上所有格子需要同时被更新：你不能先更新某些格子，然后使用它们的更新后的值再更新其他格子。
  • 本题中，我们使用二维数组来表示面板。原则上，面板是无限的，但当活细胞侵占了面板边界时会造成问题。你将如何解决这些问题？

方法1：（0ms）

    public static void gameOfLife(int[][] board) {
        int[][] map = new int[board.length][board[0].length];
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                int row = Math.max(i - 1, 0);
                int col = Math.max(j - 1, 0);
                int src = board[i][j];
                int count = 0;
                while (row < board.length && col < board[0].length){
                    count += board[row][col];
                    col++;
                    if (col == j + 2 || col == board[0].length){
                        row++;
                        col = Math.max(j - 1, 0);
                    }
                    if (row == i + 2 || row == board.length){
                        break;
                    }
                }
                count -= src;
                if (src == 1 && count == 1) {
                    map[i][j] = 0;
                }else if (src == 1 && (count == 2 || count == 3)){
                    map[i][j] = 1;
                }else if (src == 1 && count > 3){
                    map[i][j] = 0;
                }else if (src == 0 && count == 3){
                    map[i][j] = 1;
                }
            }
        }
//        board = map;
//        for (int[] ints : board) {
//            System.out.println(Arrays.toString(ints));
//        }
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                board[i][j] = map[i][j];
            }
        }
    }

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1529689.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Science：量子纠缠突破成像极限

Science：量子纠缠突破成像极限

研究专家指出&#xff0c;量子物理学的一些核心特质&#xff0c;如粒子纠缠&#xff0c;为解决一个困扰显微技术领域多年的难题提供了新的思路&#xff1a;如何在极小的尺度上获得更清晰的图像。 这项创新性的研究通过利用纠缠光子&#xff0c;开发出了一种新技术&#xff0c;能…
阅读更多...
Web前端-HTML

Web前端-HTML

HTML 负责页面的结构&#xff08;页面的元素和内容&#xff09; HTML由标签组成&#xff0c;标签都是预定义好的。例如<a>展示超链接&#xff0c;使用<img>展示图片&#xff0c;<vedio>展示视频。 HTML代码直接在浏览器中运行&#xff0c;HTML标签由浏览器…
阅读更多...
在微信小程序中或UniApp中自定义tabbar实现毛玻璃高斯模糊效果

在微信小程序中或UniApp中自定义tabbar实现毛玻璃高斯模糊效果

backdrop-filter: blur(10px); 这一行代码表示将背景进行模糊处理&#xff0c;模糊程度为10像素。这会导致背景内容在这个元素后面呈现模糊效果。 background-color: rgb(255 255 255 / .32); 这一行代码表示设置元素的背景颜色为白色&#xff08;RGB值为0, 0, 0&#xff09;&a…
阅读更多...
行业模板｜DataEase制造行业大屏模板推荐

行业模板｜DataEase制造行业大屏模板推荐

DataEase开源数据可视化分析平台于2022年6月发布模板市场&#xff08;https://templates-de.fit2cloud.com&#xff09;&#xff0c;并于2024年1月新增适用于DataEase v2版本的模板分类。模板市场旨在为DataEase用户提供专业、美观、拿来即用的大屏模板&#xff0c;方便用户根据…
阅读更多...
Stable Diffusion WebUI 生成参数：高清修复/高分辨率修复（Hires.fix）

Stable Diffusion WebUI 生成参数：高清修复/高分辨率修复（Hires.fix）

本文收录于《AI绘画从入门到精通》专栏&#xff0c;专栏总目录&#xff1a;点这里。 大家好&#xff0c;我是水滴~~ 在本篇文章中&#xff0c;我们将深入探讨 Stable Diffusion WebUI 的一个引人注目的生成参数——高分辨率修复&#xff08;Hires.fix&#xff09;。我们将逐一…
阅读更多...
添加与搜索单词 - 数据结构设计

添加与搜索单词 - 数据结构设计

题目链接 添加与搜索单词 - 数据结构设计 题目描述 注意点 addWord 中的 word 由小写英文字母组成search 中的 word 由 ‘.’ 或小写英文字母组成1 < word.length < 25 解答思路 为了加快查询速度&#xff0c;可以使用字典树存储单词&#xff0c;基本结构是&#xf…
阅读更多...
Linux: network: firewall: firewalld 导致icmp带admin prohibited

Linux: network: firewall: firewalld 导致icmp带admin prohibited

文章目录 简介查看相关的配置产生的rule不在rule里的被拒绝重新加载iptables服务进程简介 https://firewalld.org/documentation/man-pages/firewalld.zone.html 最近遇到一个主机主动回icmp，destination unreachable的错误包，而且里面的code是 administratively prohibited…
阅读更多...
Flutter与Xamarin跨平台APP开发框架的区别

Flutter与Xamarin跨平台APP开发框架的区别

嘿&#xff0c;各位亲爱的朋友们&#xff01;大家好&#xff0c;我是咕噜铁蛋&#xff01;今天我们要探讨的话题是&#xff1a;Flutter与Xamarin这两款热门的跨平台APP开发框架。我深知选择合适的开发工具对于开发者来说有多么重要。那么&#xff0c;当我们需要开发跨平台应用时…
阅读更多...
[Qt项目实战]Qt实现美松标签打印机标签二维码打印（QR混排模式+页打印模式）

[Qt项目实战]Qt实现美松标签打印机标签二维码打印（QR混排模式+页打印模式）

1、硬件信息、环境参数及配套资料 1.1 打印机信息及开发环境 打印机 美松标签打印机串口/USB通讯Qt5.9 64位程序 1.2 打印机配套开发资料 打印机主要配套测试工具、开发SDK及驱动等&#xff0c;均由厂家提供。 开发Demo及动态库&#xff1a;MsPrintSDK-DLL-V2.2.2.5 链接&…
阅读更多...
只需3步，使用Stable Diffusion无限生成AI数字人视频

只需3步，使用Stable Diffusion无限生成AI数字人视频

基本方法 搞一张照片&#xff0c;搞一段语音&#xff0c;合成照片和语音&#xff0c;同时让照片中的人物动起来&#xff0c;特别是头、眼睛和嘴。 语音合成 语音合成的方法很多&#xff0c;也比较成熟了&#xff0c;大家可以选择自己方便的&#xff0c;直接录音也可以&#…
阅读更多...
Linux TCP参数——tcp_allowed_congestion_control

Linux TCP参数——tcp_allowed_congestion_control

tcp_allowed_congestion_control 设置允许普通进程使用的拥塞控制算法。这个参数的值阈是tcp_available_congestion_control参数的子集。默认值为"reno"加上tcp_congestion_control参数设置的算法。 reno 慢启动阶段&#xff1a;在开始的时候&#xff0c;cwnd按指数…
阅读更多...
创建自己的“百度网盘”（部署owncloud）

创建自己的“百度网盘”（部署owncloud）

[rootlocalhost html]# cd /root/[rootlocalhost ~]# wget https://download.com/server/stable/owncloud-10.12.0.zip --no-check-certificate #下载当前的owncloud代码包[rootlocalhost ~]# yum -y install unzip #安装解压工具[rootlocalhost ~]# unzip owncloud-10.12.0.zi…
阅读更多...
BetterDisplay Pro for Mac(显示器校准软件) v2.0.11激活版

BetterDisplay Pro for Mac(显示器校准软件) v2.0.11激活版

BetterDisplay Pro是一款由waydabber开发的Mac平台上的显示器校准软件&#xff0c;可以帮助用户调整显示器的颜色和亮度&#xff0c;以获得更加真实、清晰和舒适的视觉体验。 软件下载&#xff1a;BetterDisplay Pro for Mac v2.0.11激活版 以下是BetterDisplay Pro的主要特点&…
阅读更多...
【数据分析可视化】动态生成柱状图

【数据分析可视化】动态生成柱状图

import pandas as pd import matplotlib.pyplot as plt import matplotlib.ticker as ticker from matplotlib.animation import FuncAnimation import matplotlib.patches as mpatches from matplotlib.animation import FFMpegWriter# 定义一个函数&#xff0c;用于生成…
阅读更多...
开源模型应用落地-安全合规篇-模型输出合规性检测（三）

开源模型应用落地-安全合规篇-模型输出合规性检测（三）

一、前言 为什么我们需要花大力气对用户输入的内容和模型生成的输出进行合规性检测，一方面是严格遵守各项法规要求，具体如下：互联网信息服务深度合成管理规定https://www.gov.cn/zhengce/zhengceku/2022-12/12/content_5731431.htm ​ 其次，受限于模型本身的一些缺陷，…
阅读更多...
智能合约 之 ERC-20介绍

智能合约 之 ERC-20介绍

什么是ERC20 ERC20全称为Ethereum Request for Comment 20&#xff0c;是一种智能合约标准&#xff0c;用于以太坊网络上的代币发行 姊妹篇 - 如何部署ERC20 ERC20的应用场景 代币化资产&#xff0c;例如&#xff1a;USDT 是一种以美元为背书的ERC20代币&#xff0c;每个USDT代…
阅读更多...
Unity 实现双屏或多屏内容展示

Unity 实现双屏或多屏内容展示

在某些应用场景&#xff0c;一个应用可能需要使用多个显示器显示。 Unity支持最多8个不同显示器同时显示应用程序中八个摄像头的视图&#xff0c;如下图&#xff1a; 具体实现如下&#xff1a; 1、在Hiearchy面板上点击鼠标右键->Camera,创建多一个Camera,如图&#xff1a…
阅读更多...
Android Studio Gradle设置查看全部task

Android Studio Gradle设置查看全部task

如果你在 Android Studio 的 Gradle 窗口中看不到所有的任务&#xff0c;你可以尝试以下步骤来解决这个问题 android studio 版本&#xff1a; Android Studio Iguana | 2023.2.1 Build #AI-232.10227.8.2321.11479570, built on February 22, 2024 打开 Android Studio 的设置…
阅读更多...
深入探讨Python中的文件操作与文件IO操作【第141篇—Python实现】

深入探讨Python中的文件操作与文件IO操作【第141篇—Python实现】

&#x1f47d;发现宝藏 前些天发现了一个巨牛的人工智能学习网站&#xff0c;通俗易懂&#xff0c;风趣幽默&#xff0c;忍不住分享一下给大家。【点击进入巨牛的人工智能学习网站】。 深入探讨Python中的文件操作与文件IO操作 在Python编程中&#xff0c;文件操作和文件IO操作…
阅读更多...
maven手动上传的第三方包 打包项目报错 Could not find xxx in central 解决办法

maven手动上传的第三方包 打包项目报错 Could not find xxx in central 解决办法

背景: 在Maven私服手动上传了第三方的jar包, 只有jar包, 没有pom文件, 项目在ide中可以正常编译启动,但打包报错无法找到jar包 解决办法: 上传jar包的时候, 点击生成pom. 则打包的时候不会报错
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023