题目链接

添加与搜索单词 - 数据结构设计

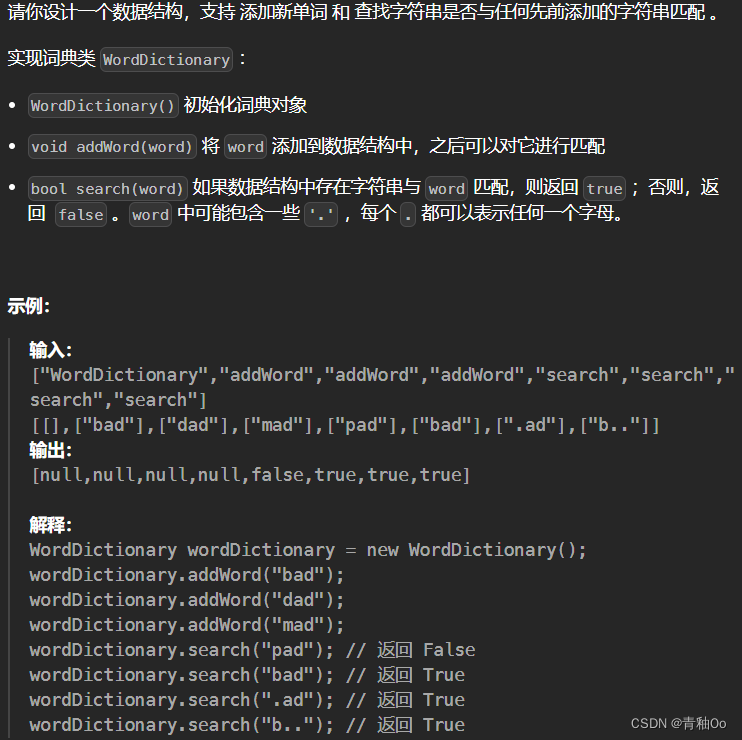
题目描述

注意点

• addWord 中的 word 由小写英文字母组成
• search 中的 word 由 ‘.’ 或小写英文字母组成
• 1 <= word.length <= 25

解答思路

• 为了加快查询速度，可以使用字典树存储单词，基本结构是：字典树Trie是由isLast（判断当前字符是否作为单词的最后一位）和大小为26的Trie数组child（存储按相应组合到达该树后所有可能的字符子树）组成
• 在写入字典树时，根据当前字符c对应的位置（c - ‘a’）找到当前单词路径是否存在树，如果不存在则新建，然后将trie[c - ‘a’]设置为当前树trie，重复此过程即可，注意当到达单词最后一位时，需要将当前树trie.isLast设置为true
• 在寻找单词是否存在时，当有’.'出现，其可以代表任意字符，需要将当前树trie的26棵子树都进行判断，任意一个成功找到说明单词存在。所以使用深度优先遍历寻找单词

代码

class WordDictionary {
    Trie[] root;

    public WordDictionary() {
        root = new Trie[26];
    }
    
    public void addWord(String word) {
        Trie[] trie = root;
        for (int i = 0; i < word.length(); i++) {
            int idx = word.charAt(i) - 'a';
            if (trie[idx] == null) {
                trie[idx] = new Trie();
            }
            if (i == word.length() - 1) {
                trie[idx].isLast = true;
            }
            trie = trie[idx].child;
        }
    }
    
    public boolean search(String word) {
        return dfs(root, word, 0);
    }

    public boolean dfs(Trie[] trie, String word, int loc) {
        char c = word.charAt(loc);
        if (c != '.') {
            int idx = c - 'a';
            // 字典树中无该字符
            if (trie[idx] == null) {
                return false;
            }
            // 判断字典树中该字符是否作为单词末尾
            if (loc == word.length() - 1) {
                return trie[idx].isLast;
            }
            return dfs(trie[idx].child, word, loc + 1);
        }
        // '.'可以代表任何字符
        for (int i = 0; i < 26; i++) {
            // 字典树中无该字符
            if (trie[i] == null) {
                continue;
            }
            boolean b = false;
            if (loc == word.length() - 1) {
                // 判断字典树中该字符是否作为单词末尾
                b = trie[i].isLast;
            } else {
                // 继续深搜寻找单词后面的字符
                b = dfs(trie[i].child, word, loc + 1);
            }
            // 满足一种情况就成功
            if (b) {
                return true;
            }
        }
        return false;
    }
}

class Trie {
    boolean isLast;
    Trie[] child;
    
    public Trie() {
        isLast = false;
        child = new Trie[26];
    }
}

/**
 * Your WordDictionary object will be instantiated and called as such:
 * WordDictionary obj = new WordDictionary();
 * obj.addWord(word);
 * boolean param_2 = obj.search(word);
 */

关键点

• 字典树的构造过程
• 深度优先遍历的思想