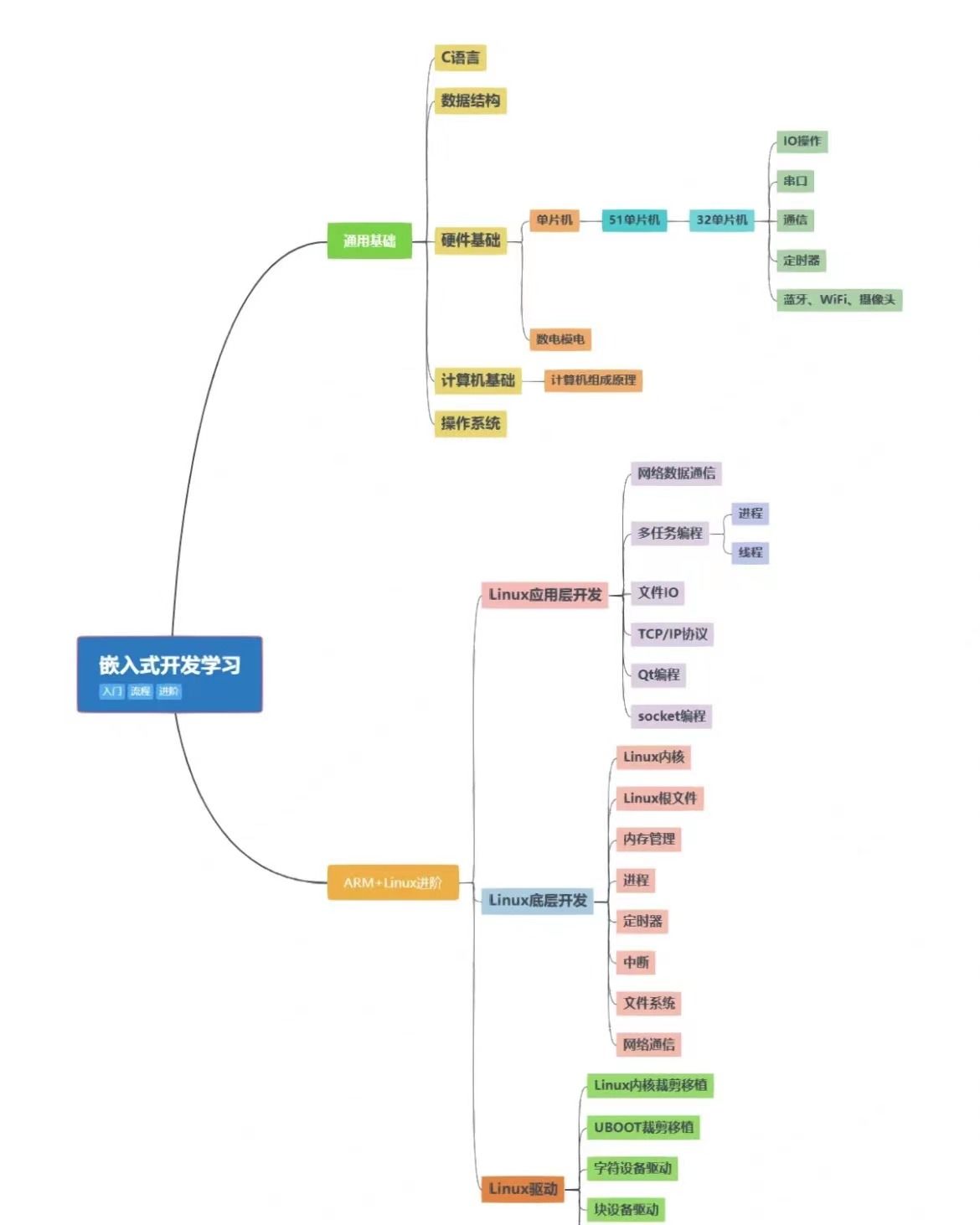
在处理器中，整数除法的成本通常是整数乘法的几倍：

• 流水线式的组合乘法器通常在不到10个周期内完成操作；
• 而对于整数除法则没有硬件支持，或者使用的迭代除法器比乘法器慢几倍。

表 1.1 比较了一些处理器上乘法和除法的时间。这张表展示了乘法和除法时间差距的增长趋势。
因此， Division by Invariant Integers using Multiplication 中提出了使用整数乘法进行任意非零整数常数和运行时不变量之间除法的算法。

文档 4. Instruction tables 中记录了更广泛的处理指令性能，其中 Intel IceLake 处理器的乘除法指令延迟和吞吐倒数如下表所示：

可以看出，在现代 CPU 处理器上除法开销大的情况并未发生改变。NVIDIA 和 AMD GPU 均不支持整数除法指令，CUDA C++ Programming Guide 5.4.1. Arithmetic Instructions 中指出整数除法和取模运算可能会编译出多达20条指令，建议开发者在某些情况下使用位运算来替代。很多深度学习框架和加速库中均采用论文所提出的算法来加速常量除法运算。

2 Mathematical notations

设 $x$ 是一个实数。那么

• $\lfloor x\rfloor$ 表示不超过 $x$ 的最大整数，
• $\lceil x\rceil$ 表示不小于 $x$ 的最小整数。

令 $\mathrm{TRUNC}(x)$ 表示 $x$ 的整数部分，向零取整。形式上，

• 如果 $x\ge 0$，则 $\mathrm{TRUNC}(x)=\lfloor x\rfloor$；
• 如果 $x\le 0$，则 $\mathrm{TRUNC}(x)=\lceil x\rceil$。

$x$ 的绝对值是 $|x|$。对于 $x>0$，$x$ 以 2 为（实数）底的对数为 ${\log }_{2}x$。

乘法写为 $x\ast y$。

如果 $x$、$y$ 和 $n$ 是整数且 $n\ne 0$，则 $x\equiv y(\mathrm{mod}n)$ 意味着 $x-y$ 是 $n$ 的倍数。

在语言定义中常见两种余数运算符。有时余数带有被除数的符号，有时带有除数的符号。我们使用 Ada 符号。
$$\begin{array}{rlr}n\mathrm{rem}d& =n-d\ast \mathrm{TRUNC}(n/d)& (\text{sign of dividend}),\\ nmodd& =n-d\ast \lfloor n/d\rfloor & (\text{sign of divisor}).\end{array}$$

Fortran 90 中的名称是 MOD 和 MODULO。在 C 语言中，对余数的定义取决于具体的实现（许多 C 实现将有符号商向零舍入并使用 $\mathrm{rem}$ 余数）。还有其他一些建议的定义[6, 7]。

如果 $n$ 是一个 udword 或 sdword，那么 $\mathrm{HIGH}(n)$ 和 $\mathrm{LOW}(n)$ 分别表示 $n$ 的最高有效半部和最低有效半部：

• $\mathrm{LOW}(n)$ 是一个 udword；
• 如果 $n$ 是 udword，$\mathrm{HIGH}(n)$ 是一个 udword ；如果 $n$ 是 sdword 则 $\mathrm{HIGH}(n)$ 是 sword。

在这两种情况下，$n=2^N\ast \mathrm{HIGH}(n)+\mathrm{LOW}(n)$。

3 Assumed instructions

建议的代码假设在 N 位机器上执行表 3.1 中的操作。某些原语，如加载常量和操作数，在符号中是隐含的，并且不包含在操作计数中。

第8节中的算法要求能够对两个双字进行加减运算，得到一个双字结果；这通常会扩展为2-4条指令。

处理常数除数的算法需要在编译时对 udword 进行算术运算。

处理运行时不变除数的算法需要取一个正整数以2为底的对数（有时向上取整，有时向下取整），并需要将一个 udword 除以一个 uword。如果这些算法只针对常数除数，那么这些操作只需要在编译时进行。如果该架构有一个前导零计数（LDZ）指令，那么可以从以下方式中找到这些对数
$$\begin{array}{rl}\lceil {\log }_{2}x\rceil & =N-\mathrm{LDZ}(x-1),\\ \lfloor {\log }_{2}x\rfloor & =N-1-\mathrm{LDZ}(x)(1\le x\le 2N-1).\end{array}$$

某些算法可能会产生诸如 $\mathrm{SRL}(x,0)$ 或 $-(x-y)$ 等表达式；优化器应该进行显而易见的简化。一些描述显示了 $2^N$ 的加法或减法，这实际上是一个无操作（no-op）。

如果一个架构缺少算术右移，则可以根据下面的等式来计算它：

$$\mathrm{SRA}(x,\ell )=\mathrm{SRL}(x+2^{N-1},\ell )-2^{N-1-\ell }\text{whenever }0\le n<2^N$$

如果一个架构只有 $\mathrm{MULSH}$ 和 $\mathrm{MULUH}$ 中的一个，那么另一个可以通过以下方式计算得出：

$$\mathrm{MULUH}(x,y)=\mathrm{MULSH}(x,y)+\mathrm{AND}(x,\mathrm{XSIGN}(y))+\mathrm{AND}(y,\mathrm{XSIGN}(x))$$
对于任意 N 位模式的 $x$，$y$（在 $\mathrm{MULUH}$ 中被解释为 uword，在 $\mathrm{MULSH}$ 中被解释为 sword）。

4 Unsigned division

假设我们想要编译一个无符号除法 $q=\lfloor n/d\rfloor$，其中 $0<d<2^N$ 是一个常数或运行时不变量，$0\le n<2^N$ 是变量。
让我们尝试找到 $1/d$ 的一个有理近似 $m/2^{N+\ell }$，使得

$$\lfloor \frac{n}{d}\rfloor =\lfloor \frac{m\ast n}{2^{N+\ell }}\rfloor \text{whenever }0\le n<2^N$$

将 $n=d$ 代入上式中显示我们需要 $2^{N+\ell }\le m\ast d$。设置 $n=q\ast d-1$ 显示 $2^{N+\ell }\ast q>m\ast (q\ast d-1)$。乘以 $d$ 得出 $(m\ast d-2^{N+\ell })\ast (q\ast d-1)<2^{N+\ell }$。 如果 $m\ast d-2^{N+\ell }\le 2$，则对于所有小于 $2^N$ 的 $q\ast d-1$ 的值，这个不等式都成立。下面的定理 4.2 声明这些条件是充分的，因为当 $n<2^N$ 时，最大相对误差（$2^N$分之一）太小，不足以影响商。

定理 4.2 假设 $m$、$d$、$\ell$ 是非负整数，使得 $d\ne 0$ 且
$$2^{N+\ell }\le m\ast d\le 2^{N+\ell }+2^{\ell }\text{(4.3)}$$

那么对于每一个整数 $n$ 且 $0\le n<2^N$ 有 $\lfloor \frac{n}{d}\rfloor =\lfloor m\ast n/2^{N+\ell }\rfloor$。

证明： 定义 $k=m\ast d-2^{N+\ell }$。那么根据假设有 $0\le k\le 2^{\ell }$。给定 $0\le n<2^N$ 的 $n$，写作 $n=q\ast d+r$，其中 $q=\lfloor n/d\rfloor$ 且 $0\le r\le d-1$。我们必须证明 $q=\lfloor m\ast n/2^{N+\ell }\rfloor$。通过计算得出

$$\begin{array}{rl}\frac{m\ast n}{2^{N+\ell }}-q& =\frac{m\ast d}{d}\ast \frac{n}{2^{N+\ell }}-q\\ & =\frac{k+2^{N+\ell }}{d}\ast \frac{n}{2^{N+\ell }}-q\\ & =\frac{k\ast n}{d\ast 2^{N+\ell }}+\frac{n}{d}-\frac{n-r}{d}\\ & =\frac{k}{2^{\ell }}\ast \frac{n}{2^N}\ast \frac{1}{d}+\frac{r}{d}\end{array}$$

因为 $0\le k\le 2^{\ell }$，$0\le n<2^N$，$0\le r\le d-1$，
$$\begin{array}{rl}\frac{0}{2^{\ell }}\ast \frac{0}{2^N}\ast \frac{1}{d}+\frac{0}{d}\le & \frac{k}{2^{\ell }}\ast \frac{n}{2^N}\ast \frac{1}{d}+\frac{r}{d}\le \frac{2^{\ell }}{2^{\ell }}\ast \frac{2^N-1}{2^N}\ast \frac{1}{d}+\frac{d-1}{d}\\ 0\le & \frac{k}{2^{\ell }}\ast \frac{n}{2^N}\ast \frac{1}{d}+\frac{r}{d}\le \frac{2^N-1}{2^N}\ast \frac{1}{d}+\frac{d-1}{d}\\ 0\le & \frac{k}{2^{\ell }}\ast \frac{n}{2^N}\ast \frac{1}{d}+\frac{r}{d}\le 1-\frac{1}{2^N\ast d}\\ 0\le & \frac{k}{2^{\ell }}\ast \frac{n}{2^N}\ast \frac{1}{d}+\frac{r}{d}<1\end{array}$$
这个差值是非负的，并且不超过 1。

如果不等式（4.3）成立，定理 4.2 允许用 $m\ast n/2^{N+\ell }$ 的乘法来替代除以 $d$。一般来说，我们要求 $2^{\ell }\ge d-1$ 以确保在区间 $[2^{N+\ell },2^{N+\ell }+2^{\ell }]$ 中存在 $d$ 的适当倍数。为了与有符号除法的算法（第5节和第6节）兼容，选择 $m\ast d>2^{N+\ell }$，尽管定理 4.2 允许相等。由于 $m$ 几乎可以大到 $2^{N+1}$，我们不直接乘以 $m$，而是分别乘以 $2^N$ 和 $m-2^N$。这引出了图 4.1 中的代码。在计算仅依赖于除数的常数之后，每个商的成本为1次乘法、2次加法/减法以及2次移位。

图 4.1 的解释：

• 如果 $d=1$，那么 $\ell =0$，所以 $m^{\prime }=1$ 且 $s{h}_1=s{h}_2=0$。代码计算 $t_1=\lfloor 1\ast n/2^N\rfloor =0$ 和 $q=n$。
• 若 $d>1$，则 $\ell \ge 1$，故 $s{h}_1=1$ 且 $s{h}_2=\ell -1$。由于 $m^{\prime }\le \frac{2^N\ast (2^{\ell }-d)}{d}+1\le \frac{2^N\ast (d-1)}{d}+1<2^N$，$m^{\prime }$ 的值可以置于一个 uword 中。由于 $0\le t_1\le n$，$q$ 的公式简化为
  $$\begin{array}{rl}q& =\mathrm{SRL}(t_1+\mathrm{SRL}(n-t_1,1),\ell -1)\\ & =\lfloor \frac{t_1+\lfloor \frac{(n-t_1)}{2}\rfloor }{2^{\ell -1}}\rfloor \\ & =\lfloor \frac{\lfloor \frac{2\ast t_1}{2}+\frac{(n-t_1)}{2}\rfloor }{2^{\ell -1}}\rfloor \text{(4.5)}\\ & =\lfloor \frac{\lfloor (t_1+n)/2\rfloor }{2^{\ell -1}}\rfloor \\ & =\lfloor \frac{t_1+n}{2^{\ell }}\rfloor \end{array}$$

而 $t_1+n=\lfloor m^{\prime }\ast n/2^N\rfloor +n=\lfloor (m^{\prime }+2^N)\ast n/2^N\rfloor$。设 $m=m^{\prime }+2^N=\lfloor 2^{N+\ell }/d\rfloor +1$。由于 $2^{N+\ell }<m\ast d\le 2^{N+\ell }+2^{\ell }$，且 $d\le 2^{\ell }$，
$$\begin{array}{rl}{2}^{N+\ell }/d-1& \le m-1\le 2^{N+\ell }/d\\ 2^{N+\ell }-d& \le m\ast d-d\le 2^{N+\ell }\\ 2^{N+\ell }& \le m\ast d\le 2^{N+\ell }+d\\ 2^{N+\ell }& \le m\ast d\le 2^{N+\ell }+2^{\ell }\end{array}$$
因此满足定理 4.2 的假设。

注意： 从概念上讲，$q$ 是 $\mathrm{SRL}(n+t_1,\ell )$，就像在 (4.5) 中一样。不要这样计算 $q$，因为 $n+t_1$ 可能会溢出 $N$ 位，且移位计数可能会越界。

改进： 如果 $d$ 是常数且为2的幂，则用移位替换除法。

改进： 如果 $d$ 是常数且 $m=m^{\prime }+2^N$ 是偶数，则将 $m/2^{\ell }$ 约简到最低项。原始乘数约简后在 $N$ 位内。在极少数情况下（例如，在 32 位机器上 $d=641$，在 64 位机器上 $d=274177$），最终的移位为零。

改进。 如果 $d$ 是常数且为偶数，则对某个 $e>0$ 重写 $\lfloor \frac{n}{d}\rfloor =\lfloor \frac{\lfloor n/2^e\rfloor }{d/2^e}\rfloor$。然后可以使用 $\mathrm{SRL}$ 计算 $\lfloor n/2^e\rfloor$。由于 $n/2^e<2^{N-e}$，乘数所需的精度比之前少。

这些思想体现在图 4.2 中，它生成了 $n/d$ 的代码，其中 $n$ 是无符号的，$d$ 是常数。

以下三个示例阐述了图 4.2 中的情况。所有示例都采用无符号 32 位算术。

示例：$q=\lfloor n/10\rfloor$。CHOOSE MULTIPLIER 找到 $m_{\mathrm{low}}=(2^{36}-6)/10$ 和 $m_{\mathrm{high}}=(2^{36}+14)/10$。 经过一轮除以2的操作后，它返回 $(m,3,4)$，其中 $m=(2^{34}+1)/5$。推荐的代码 $q=\mathrm{SRL}(\mathrm{MULUH}((2^{34}+1)/5,n),3)$ 消除了预先的0位移。见表 11.1。

示例：$q=\lfloor n/7\rfloor$。这里 $m=(2^{35}+3)/7>2^{32}$。本示例使用图 4.1 中较长的序列。

示例：$q=\lfloor n/14\rfloor$。CHOOSE MULTIPLIER 首先返回当 $d=7$ 时相同的乘数。 推荐的代码使用2和7的独立除法：

$$q=\mathrm{SRL}(\mathrm{MULUH}((2^{34}+5)/7,\mathrm{SRL}(n,1)),2).$$

本算法和后续算法共享的程序 CHOOSE MULTIPLIER 如图 6.2 所示。

因为 $N+s{h}_{post}\le \ell +prec$，所以 $N+s{h}_{post}-prec\le \ell$。
$$2^{N+s{h}_{post}}\ast (1+2^{-prec})\le 2^{N+s{h}_{post}}+2^{\ell }$$
又因为 $0\le s{h}_{post}\le \ell$，所以
$$2^{N+s{h}_{post}}\ast (1+2^{-prec})\le 2^{N+\ell }+2^{\ell }$$
不等式（4.3）的上界成立。

因为 $2^{\ell -1}<d$ 且 $d\le 2^{prec}$， 所以 $\ell -1<prec$，所以 $2^{-prec}<2^{1-\ell }$。
$$m<2^{N+s{h}_{post}}\ast (1+2^{1-\ell })/d$$
因为 $2^{\ell -1}<d\le 2^{\ell }$ 且 $2^{1-\ell }\le 1$，所以 $1+2^{1-\ell }\le 2$。可得
$$2^{N+s{h}_{post}}\ast (1+2^{1-\ell })/d\le 2^{N+s{h}_{post}}\ast 2/d$$
又因为 $d\le 2^{\ell }$，所以
$$2^{N+s{h}_{post}+1}/d\le 2^{N+s{h}_{post}-\ell +1}$$
因此，$2^{N+s{h}_{post}}\ast (1+2^{1-\ell })/d\le 2^{N+s{h}_{post}-\ell +1}$。

注意：略去5到9节中商向零取整的有符号除法、商向负无穷大取整的有符号除法、udword 除以运行时不变的 uword，以及先验已知余数为零的除法。

10 Implementation in GCC

作者在可自由使用的 GCC 编译器[21]中实现了常数除数的算法，扩展了其与机器和语言无关的内部代码生成。 并且还对一些机器描述符或 md 文件进行了轻微的机器依赖的修改，以获得最优的代码。GCC 支持的所有语言和几乎所有处理器都将受益。 相关更改计划包含在 GCC 2.6中。

为了生成 N 位数除法的代码，CHOOSE MULTIPLIER 函数需要执行 ($2N$) 位算术运算。这使得该程序比图 6.2中显示的更复杂。

根据操作的位大小选择最佳指令是一个棘手的问题，作者花了相当长的时间：

• 对于某些架构，选择具有最小可用精度的乘法指令很重要。
• 在其他架构上，可以通过一系列加法、减法和移位更快地执行乘法。

作者还没有实现任何针对运行时不变除数的算法。只有少数架构（AMD 29050、英特尔 x86、摩托罗拉 68k 和88110，以及在某种程度上的 IBM POWER）具有足够的硬件支持来使这种实现可行，即可以用于整数对数计算的指令，以及 ($2N$) 位/$N$ 位除法指令。即使有硬件支持，也必须小心，确保转换真正改进了代码；例如，可能需要执行很多次循环才能确保较快的循环体超过循环头中乘数的计算成本。

11 Results

图 11.1 提供了一个编译时间常数除法器的例子，它在所有最新的处理器实现上都获得了显著的加速。该程序将二进制数转换为十进制字符串。它为每个输出数字计算一个商和一个余数。

表 11.1 展示了为 Alpha、MIPS、POWER 和 SPARC 生成的汇编代码。这里没有显式的除法。尽管最初是单独计算的，但商和余数计算已合并（通过 GCC 的公共子表达式消除过程）。

unsigned int 数据类型在所有四种架构上均为32位，但 Alpha 是一种64位架构。Alpha 的代码比其他的长，因为它使用
$$4\ast [(2^{16}+1)\ast (2^8+1)\ast (4\ast [4\ast (4\ast x-x)+x]-x)]+x$$
将 $(2^{34}+1)/5$ 乘以 $x$，而不是更慢的、需要 23 个周期的mulq。这说明这些算法所需的乘法有时可以通过一系列的移位、加法和减法快速计算[5]，因为小常数除数的乘数在二进制模式上有规律。

表 11.2 比较了有除法消除算法和没有除法消除算法的基转换例程在一些处理器实现上的时间。转换的数字是一个完整的32位数，足以隐藏测量中的程序调用开销。

作者还运行了 SPEC’92 的整数基准测试。对于大多数程序来说，改进微不足道；观察到的最佳改进仅为3%左右。一些涉及哈希的基准测试显示出高达约30%的提升。作者预计在一些数论代码上会有显著的提升。

参考资料：

• Division by Invariant Integers using Multiplication
• Improved division by invariant integers
• C++干货系列——从编译期常量谈到constexpr(二)
• Integer Division by Constants: Optimal Bounds
• lemire/fast_division
• Thorius/fast_division
• Why doesn’t gcc or clang on ARM use “Division by Invariant Integers using Multiplication” trick?
• Perform integer division using multiplication [duplicate]
• paddle/phi/kernels/funcs/fast_divmod.h
• paddle/phi/kernels/primitive/datamover_primitives.h
• onnxruntime/core/providers/cuda/shared_inc/fast_divmod.h
• intel/xetla/include/common/utils/fastmath.hpp
• How to find magic multipliers for divisions by constant on a GPU?
• [原创]加减乘除反汇编笔记与MagicNumber探究记录
• Java 源码 - java.lang.Integer
• 除以二
• C/C++除数为整数常量（但不是2的幂次）时，优化得div指令都没了是什么原理？
• 编译技术-除常数优化
• 即，令，当，这些数学用语在英文论文中如何表示？
• 英语分数的表达,特别是分母比较大的怎么表达 比如： 2/37 2/115 3/1112
• What has a better performance: multiplication or division?
• 4. Instruction tables
• 『扩展欧几里得算法 Extended Euclid』
• 擴展歐基里德算法 (Extended Euclidean algorithm)
• The integer division algorithm of Intel’s x86 processors
• x86汇编_MUL/IMUL乘法指令_笔记52
• integer division and modulo
• Quick ALU Performance multiply/division investigation
• Most efficient way of dividing by power of two
• Fast integer division and modulo with a const runtime divisor
• Floating Point and Integer Arithmetic Benchmark
• Achieved IOPs
• Integer division problem
• 5.4.1. Arithmetic Instructions