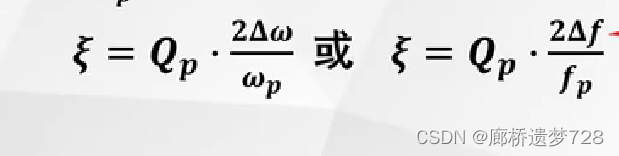并联谐振回路概述
串联谐振回路适用于低内阻电源(理想电压源)。而对于大内阻电源,则适合采用并联谐振回路。
并联谐振回路:指电感线圈L、电容器C和外加信号源相互并联的振荡回路。同样,由于电容器C的损耗很小,可以认为损耗电阻集中于电感线圈L。
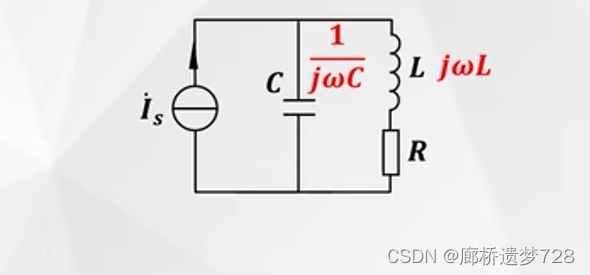
如图所示,LC并联端口阻抗为:
一般情况下损耗电阻R很小,故上式可化简为:
为使式子简洁,常将其变换为导纳的形式:
其中:G=RC/L为电导,B为电纳。由导纳的式子可将其看成三个元件并联,得到如下转换:
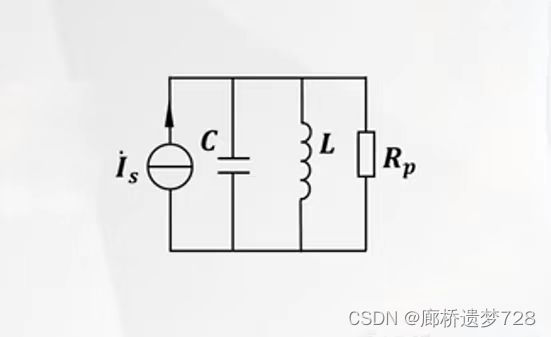
其中,
谐振条件
由阻抗可知,并联谐振时,呈现纯电阻,且阻抗为最大值(即电纳B=0,回路导纳Y=Gp为最小值)。
将记为谐振时的角频率。
| 呈现感性 | B<0 | |
| 纯阻抗 | B=0 | |
| 呈现容性 | B>0 |
谐振频率(满足):
由得,谐振时B=0,故
,得
,则
。
品质因数
定义为:
其中为特性阻抗。将上式中的损耗电阻R用谐振电阻Rp替换,可得:
对谐振时的电感、电容支路,其电流值如下:
可以看出谐振时电感支路与电流支路的电流幅值相等,相位相反,且为外加信号源电流的Qp倍。因此,并联谐振也称为电流谐振。
广义失谐系数
用来表示回路失谐大小的量。并联谐振回路用失谐时的电纳比谐振时的电导
定义为:
当失谐不大时:
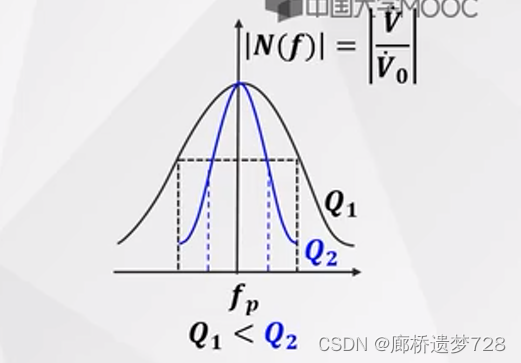
谐振曲线
串联回路用电流比来表示,并联回路用电压比来表示。
通频带:指电流下降到谐振电流的0.707倍时的频率范围。
相频特性曲线