我们将主要使用交叉熵成本来解决学习减速的问题。然而，我想简要描述另一种解决方法，基于所谓的 softmax 层神经元。在本章的剩余部分，我们实际上不会使用 softmax 层，因此如果你时间紧迫，可以跳到下一节。然而，softmax 仍然值得理解，部分原因是它本身很有趣，另一部分原因是我们将在后面讨论深度神经网络时使用 softmax 层。

Softmax 的思想是为我们的神经网络定义一种新类型的输出层。它的开始方式与 sigmoid 层相同，通过形成加权输入来开始。$z_j^L={\sum }_k{w}_{jk}^L{a}_k^{L-1}+b_j^L$然而，我们不应用 sigmoid 函数来获得输出。相反，在 softmax 层中，我们将所谓的 softmax 函数应用于 $z_j^L$。根据此函数，第 j 个输出神经元的激活 $a_j^L$是
$$a_j^L=\frac{e^{z_j^L}}{{\sum }_k{e}^{z_k^L}},\text{\hspace{1em}(78)}$$

如果您对 softmax 函数不熟悉，方程（78）可能看起来很难理解。不明白为什么我们想要使用这个函数。而且这也不明显会帮助我们解决学习减速问题。为了更好地理解方程（78），假设我们有一个具有四个输出神经元和四个相应加权输入的网络，我们将它们表示为$z_1^L,z_2^L,z_3^L$ 和 $z_4^L$。在下面显示了可调节的滑块，显示了加权输入的可能值，并显示了相应的输出激活的图表。开始探索的一个好方法是使用底部滑块增加 zL4：

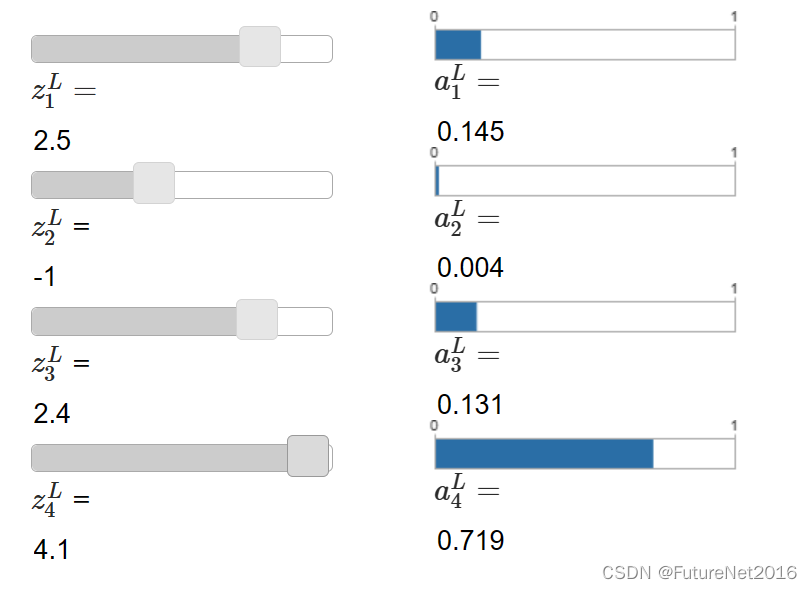
当您增加 zL4 时，您会看到相应的输出激活 aL4 增加，其他输出激活减少。类似地，如果您减少 zL4，那么 aL4 将减少，并且所有其他输出激活将增加。实际上，如果您仔细观察，您会看到在这两种情况下，其他激活的总变化完全补偿了 aL4 的变化。原因是输出激活总是保证总和为 1，我们可以使用方程（78）和一点代数来证明：
$$\sum _j{a}_j^L=\frac{{\sum }_j{e}^{z_j^L}}{{\sum }_k{e}^{z_k^L}}=1.\text{\hspace{1em}(79)}$$

因此，如果 aL4 增加，那么其他输出激活必须以相同的总量减少，以确保所有激活的总和保持为 1。当然，类似的情况也适用于所有其他激活。

方程（78）还意味着输出激活都是正的，因为指数函数是正的。将这一点与上一段的观察结合起来，我们可以看到 softmax 层的输出是一组正数，它们总和为 1。换句话说，softmax 层的输出可以被看作是一个概率分布。

softmax 层输出概率分布的事实相当令人满意。在许多问题中，将输出激活 aLj 解释为网络对正确输出为 j 的概率的估计是方便的。因此，在 MNIST 分类问题中，我们可以将 aLj 解释为网络对正确数字分类为 j 的估计概率。

相比之下，如果输出层是 sigmoid 层，那么我们肯定不能假设激活形成一个概率分布。我不会明确证明，但是应该是合理的假设，sigmoid 层的激活通常不会形成概率分布。因此，对于 sigmoid 输出层，我们没有这样简单的输出激活解释。

我们开始逐渐理解 softmax 函数和 softmax 层的行为方式。为了回顾我们的进展：方程（78）中的指数项确保所有输出激活都是正的。而方程（78）中分母的求和确保了 softmax 输出的总和为 1。因此，这种特定形式不再显得那么神秘：相反，它是一种自然的方式来确保输出激活形成一个概率分布。您可以将 softmax 视为一种重新缩放 zLj 的方式，然后将它们压缩在一起形成概率分布。

学习减速问题：我们现在已经相当熟悉 softmax 层神经元了。但我们还没有看到 softmax 层是如何让我们解决学习减速问题的。为了理解这一点，让我们定义对数似然成本函数。我们将使用 x 表示网络的训练输入，y 表示相应的期望输出。那么与此训练输入相关的对数似然成本为
$$C\equiv -\ln a_y^L.\text{\hspace{1em}(80)}$$

所以，例如，如果我们正在使用 MNIST 图像进行训练，并输入一个数字 7 的图像，那么对数似然成本就是 $-\ln a_7^L$。为了看出这是直观合理的，考虑当网络表现良好时的情况，也就是说，它对输入是数字 7 的确信度很高。在这种情况下，它将估计相应的概率 $a_7^L$ 的值接近于 1，因此成本 $-\ln a_7^L$ 将很小。相比之下，当网络表现不佳时，概率 $a_7^L$将较小，成本 $-\ln a_7^L$ 将较大。因此，对数似然成本的行为符合我们对成本函数的预期。

那么学习减速问题呢？要分析这个问题，回想一下学习减速的关键是量 $\partial C/\partial w_{jk}^L$ 和 $\partial C/\partial b_j^L$ 的行为。我不会明确地进行推导 - 我会在下面的问题中要求你来做 - 但是通过一点代数运算，你可以证明：
$$\frac{\partial C}{\partial b_j^L}=a_j^L-y_j\text{\hspace{1em}(81)}$$
$$\frac{\partial C}{\partial w_{jk}^L}=a_k^{L-1}(a_j^L-y_j)\text{\hspace{1em}(82)}$$

这些方程与我们之前分析交叉熵时获得的类似表达式相同。例如，将方程（82）与方程（67）进行比较。它们是相同的方程，尽管在后者中我对训练实例进行了平均。而且，正如在先前的分析中一样，这些表达式确保我们不会遇到学习减速。实际上，将具有对数似然成本的 softmax 输出层视为与具有交叉熵成本的 sigmoid 输出层非常相似是很有用的。

鉴于这种相似性，您应该使用 sigmoid 输出层和交叉熵，还是 softmax 输出层和对数似然呢？实际上，在许多情况下，两种方法都效果很好。在本章的其余部分，我们将使用具有交叉熵成本的 sigmoid 输出层。然后，在后面章节中，我们有时会使用具有对数似然成本的 softmax 输出层。切换的原因是使我们稍后的一些网络更类似于某些有影响力的学术论文中发现的网络。作为更一般的原则，每当您想将输出激活解释为概率时，softmax 加上对数似然都值得使用。这并不总是一个关注点，但在涉及不相交类别的分类问题（如 MNIST）中可能很有用。