[Acwing 5.多重背包]

有 $N$ 种物品和一个容量是 $V$ 的背包。

第 $i$ 种物品最多有 $s_i$ 件，每件体积是 $v_i$，价值是 $w_i$。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式

第一行两个整数，$N$，$V$，用空格隔开，分别表示物品种数和背包容积。

接下来有 $N$ 行，每行三个整数 $v_i,w_i,s_i$，用空格隔开，分别表示第 $i$ 种物品的体积、价值和数量。

输出格式

输出一个整数，表示最大价值。

数据范围

$0<N\le 1000$

$0<V\le 2000$

$0<v_i,w_i,s_i\le 2000$

提示：

本题考查多重背包的二进制优化方法。

输入样例

4 5
1 2 3
2 4 1
3 4 3
4 5 2

输出样例：

10

思路

01背包：第i种物品可以取0件、取1件。
多重背包：第 $i$ 种物品可以取 $0$ 件、取 $1$ 件、取 $2$ 件 ……取 $s_i$ 件。多重背包转化为 $01$ 背包求解:把第i种物品换成 $s$ :件 $01$ 背包中的物品，每件物品的体积为 $k\ast v$ ，价值为 $k\ast w$。$(0\le k\le s)$

对01背包和完全背包不了解的可以看一下这两篇博客
01背包
完全背包

$01$背包

	//v体积，w价值，s数量
	for (int i = 1; i <= n; i++)
		for (int j = m; j >= v[i]; j--) //循环条件保证数组下标为正
			f[j] = max(f[j], f[j - v[i]] + w[i]); //状态转移方程

多重背包

	//v体积，w价值，s数量
	for (int i = 1; i <= n; i++)
		for (int j = m; j >= v[i]; j--)
			for (int k = 0; k <= s[i] && k * v[i] <= j; j++)
				f[j] = max(f[j], f[j - k * v[i]] + k * w[i]);

优化后的朴素算法代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1010;
int f[N];

int main() {
	int n, m;
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++) {
		int v, w, s;
		scanf("%d%d%d", &v, &w, &s);
		for (int j = m; j >= 0; j--)
			for (int k = 1; k <= s && k * v <= j; k++)
				f[j] = max(f[j], f[j - k * v] + k * w);
	}
	printf("%d\n", f[m]);
	return 0;
}

二进制优化

例子

假设有50个苹果，现在要取 $n$ 个苹果 $(n\le 50)$，如何取?
朴素的做法应该是将苹果一个一个拿出来，直到 $n$ 个苹果被取出来。再假设有 $50$ 个苹果和 $6$ 只箱子，利用箱子进行某些预备工作，
可以在每个箱子中放$2^k(k\ge 0)$个苹果，
也就是$1、2、4、8、16、19$(剩余的数)，取任意 $n$ 个苹果时，只要推出几只箱子就可以了

二进制拆分思想:将第 $i$ 种物品拆分成若干件物品，每件物品的体积和价值乘以一个拆分系数$(1,2^1,2^2\dots 2^{k-1},s-2^{k+1})$，就可以转化成 $01$ 背包的物品求解例如，$s_i=12$，拆分系数为 $1,2,4,5$，转化成 $4$ 件 $01$ 背包的物品:$(v_i,w_i),(2v_i,2w_i),(4v_i,4w_i),(5v_i,5w_i)$。

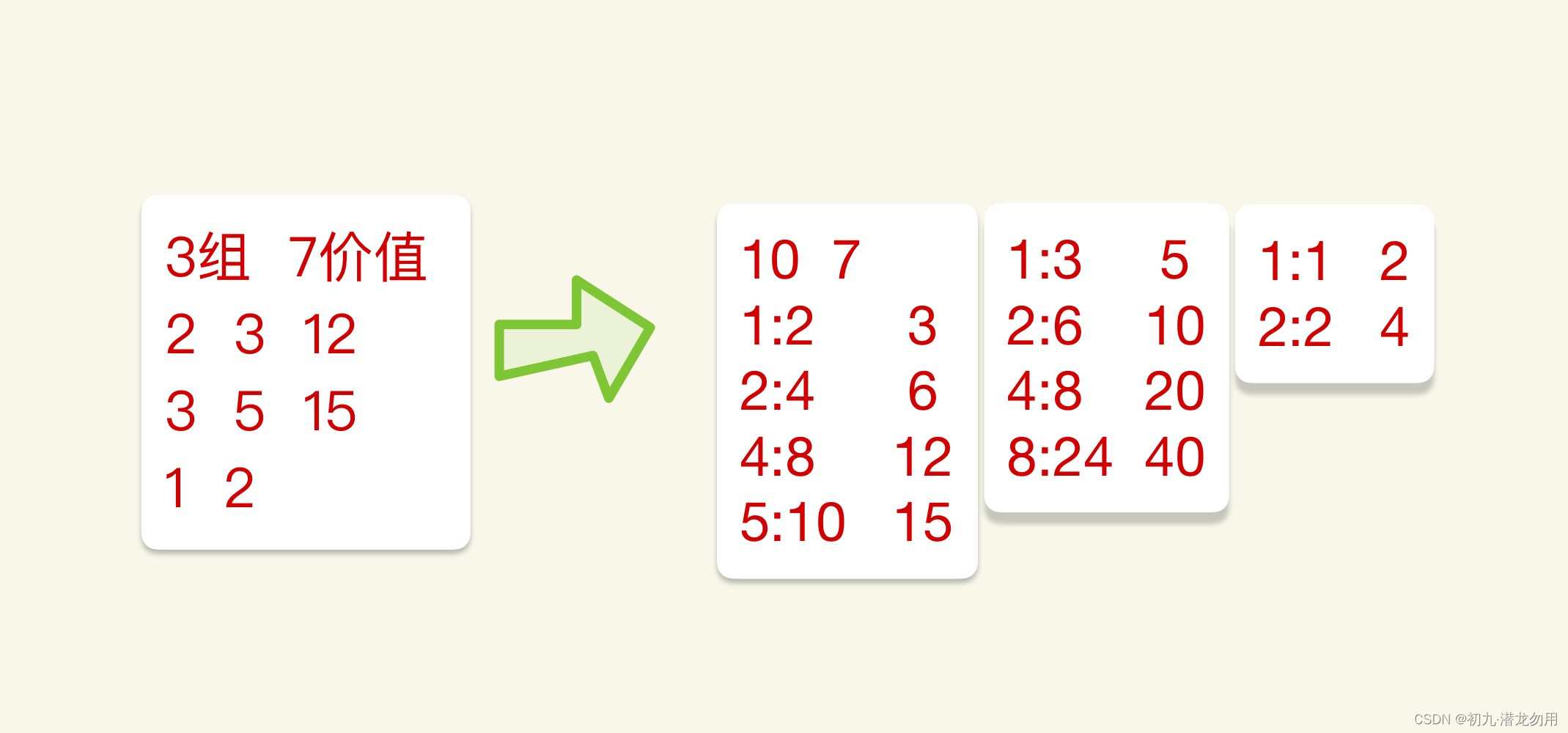
此时把原本的三组物品分割成十组，并且原来的三组分割后依然可以组合为任意个数。
比如原本体积为 $2$ 、价值为 $3$ 、个数为 $12$ 的一组分割为体积为 $1、2、4、5$ 的四组，若要最优解是原本的体积为 $8$ ,则可从分割后的四组中取体积为 $1、2、5$ 的三组即可，同理可以拼凑出任意任意体积。

二进制优化代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 2010;
int f[N],vv[N],ww[N];

int main() {
	int n, m;
	scanf("%d%d",&n,&m);
	
	int num=1;//拆分的组数的计数
	for(int i=1;i<=n;i++){
		int v,w,s;
		scanf("%d%d%d",&v,&w,&s);
		
		//这段代码本质是将原本的3种物品根据二进制拆分为10种物品
		for(int j=1;j<=s;j<<=2){
			vv[num]=j*v;//体积
			ww[num++]=j*w;//价值
			s-=j;
		}
		if(s){//若有剩余
			vv[num]=s*v;
			ww[num++]=s*w;
		}
	}
	
	//拆分为01背包后使用01背包模板即可
	for (int i = 1; i < num; i++)
		for (int j = m; j >= vv[i]; j--) 
			f[j] = max(f[j], f[j - vv[i]] + ww[i]); 
	
	printf("%d",f[m]);
	return 0;
}