🔥 个人主页: 黑洞晓威
😀你不必等到非常厉害,才敢开始,你需要开始,才会变的非常厉害。
131.分割回文串
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
示例 1:
输入:s = "aab"
输出:[["a","a","b"],["aa","b"]]
示例 2:
输入:s = "a"
输出:[["a"]]
解决思路
这个问题可以通过回溯算法来解决。回溯算法是一种搜索算法,通过尝试所有可能的情况来找到所有的解。
具体步骤如下:
- 遍历字符串
s,以每个字符为起点进行回溯搜索,找到所有可能的回文子串组合。 - 在搜索过程中,每当找到一个回文子串时,将其加入当前路径,并继续向下搜索。
- 当搜索到字符串末尾时,将当前路径加入结果列表中,并回溯到上一层继续搜索。
代码
class Solution {
List<List<String>> result = new ArrayList<>();
public List<List<String>> partition(String s) {
List<String> path = new ArrayList<>();
backTrack(s,0,path);
return result;
}
public void backTrack(String s , int start,List<String> path){
if(start >= s.length()){
result.add(new ArrayList<>(path));
}
for(int i = start;i<s.length();i++){
String ns = s.substring(start, i + 1);
if(judge(ns)){
path.add(ns);
backTrack(s,i+1,path);
path.remove(path.size()-1);
}
}
}
public boolean judge(String s){
int first = 0;
int second = s.length()-1;
while(first < second){
if(s.charAt(first) != s.charAt(second)){
return false;
}
first++;
second--;
}
return true;
}
}
450.删除二叉搜索树中的节点
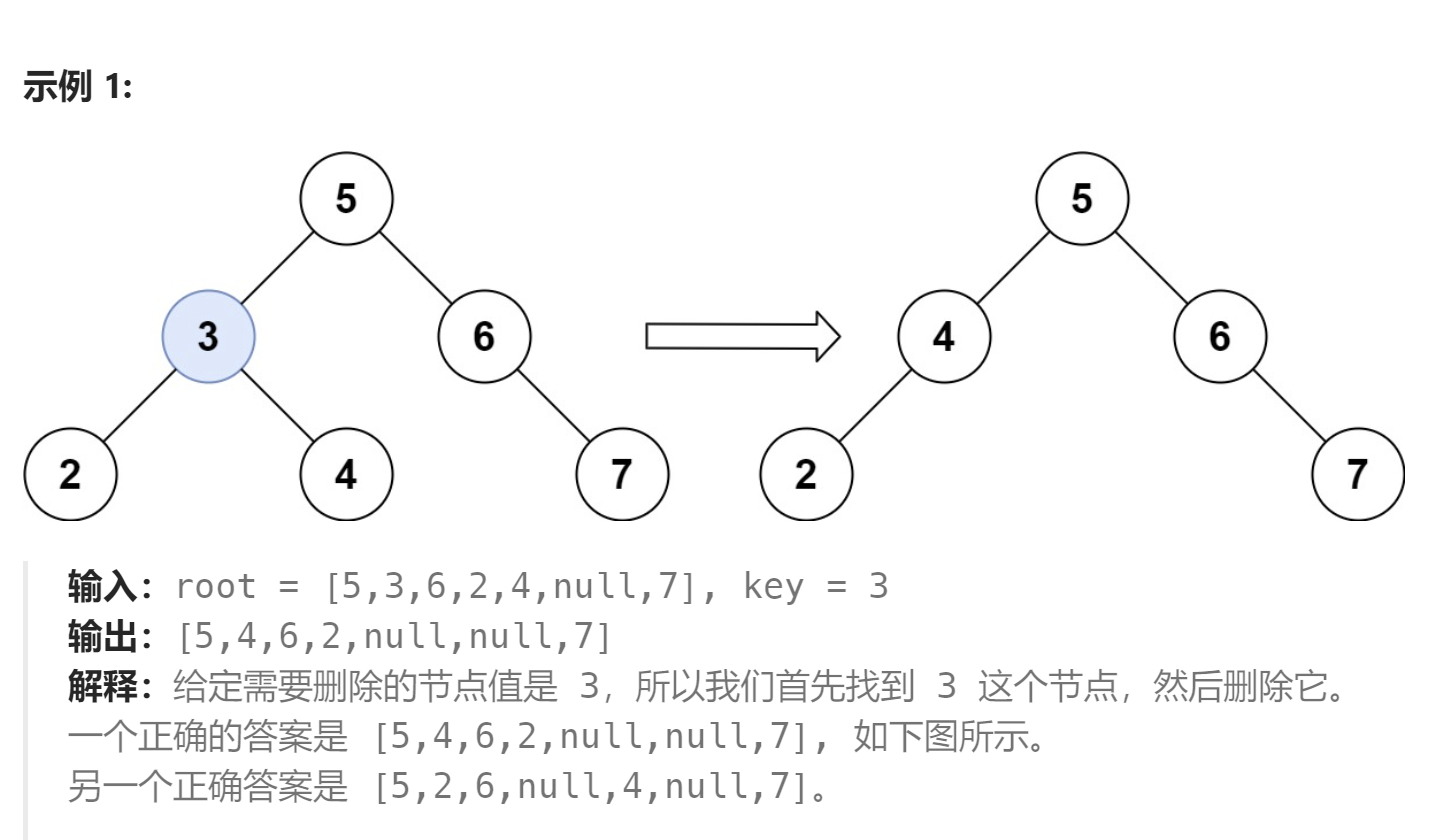
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
解决思路
- 找到需要删除的节点。
- 根据节点的情况进行删除操作:如果节点是叶子节点,则直接删除;如果节点只有一个子节点,则用子节点替换当前节点;如果节点有两个子节点,则找到右子树中的最小节点,将当前节点替换为最小节点,然后删除右子树中的最小节点。
代码
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int val) {
this.val = val;
}
}
public class DeleteNodeInBST {
public TreeNode deleteNode(TreeNode root, int key) {
if (root == null) {
return null;
}
if (key < root.val) {
root.left = deleteNode(root.left, key);
} else if (key > root.val) {
root.right = deleteNode(root.right, key);
} else {
if (root.left == null) {
return root.right;
} else if (root.right == null) {
return root.left;
}
root.val = findMin(root.right).val;
root.right = deleteNode(root.right, root.val);
}
return root;
}
private TreeNode findMin(TreeNode node) {
while (node.left != null) {
node = node.left;
}
return node;
}
public static void main(String[] args) {
TreeNode root = new TreeNode(5);
root.left = new TreeNode(3);
root.right = new TreeNode(6);
root.left.left = new TreeNode(2);
root.left.right = new TreeNode(4);
root.right.right = new TreeNode(7);
int key = 3;
DeleteNodeInBST solution = new DeleteNodeInBST();
TreeNode result = solution.deleteNode(root, key);
// 输出结果
System.out.println(result);
}
}