一、正切函数的图像性质

标准正切函数 $\tan x$ 的图像：

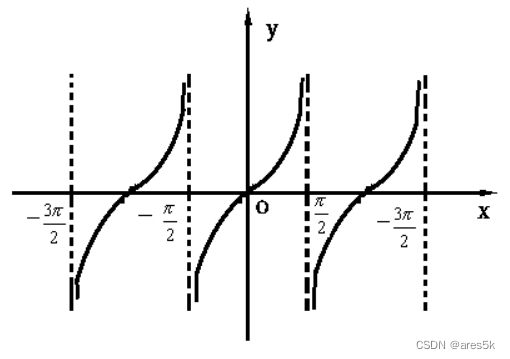
做题画图时，正切函数不需要使用五点法画图，只需要取三个点就好：$-\frac{\pi }{2}、0、\frac{\pi }{2}$ 即可，当碰见复杂的正切函数时，其解题思路和正余弦函数是完全相通的

定义域和值域

标准正切函数 $\tan x$ 的定义域为：{$x|x\ne k\pi +\frac{\pi }{2},k\in Z$}，值域：$(-\infty ,+\infty )$

周期性

标准正切函数 $\tan x$ 的周期为 $\pi$

复杂正切函数 $A\tan (\omega x+\phi )$ 的周期公式为：$T=\frac{\pi }{\omega }$

奇偶性

标准正切函数 $\tan x$ 基于原点对称，所以为奇函数

复杂正切函数 $A\tan (\omega x+\phi )$ 时，只要 $\phi$ 是 $\frac{\pi }{2}$ 的整数倍，那么这个正切函数就都是奇函数（ $\phi$ 是 $\frac{\pi }{2}$ 的奇数倍时，会发生奇变，变为 $\frac{1}{\tan \alpha }$，但这也仅仅是变为倒数，并不会影响其奇偶性），当 $\phi$ 不是 $\frac{\pi }{2}$ 的整数倍时，那这个函数就是非奇非偶函数

对称性

正切函数的没有对称轴，但是有对称中心，标准的正切函数 $\tan x$ 的对称中心为：$(\frac{k\pi }{2},0),k\in Z$

单调性

标准正切函数 $\tan x$ 在 $(-\frac{\pi }{2}+k\pi ,\frac{\pi }{2}+k\pi )$ 内单调递增

二、三角函数恒等变换公式

1. 同角齐次式

将 $\cos \alpha$ 与 $\sin \alpha$ 的分式，变为关于 $\tan$ 的式子。要求分式的分子和分母中的每一项都必须是相同的次数，也就是必须齐次。然后分子分母同除相同次数的 $\cos \alpha$

这个原理需要了解同角恒等式：$\tan \alpha =\frac{\sin \alpha }{\cos \alpha }$ 和 ${\sin }^2\alpha +{\cos }^2\alpha =1$

适合使用同角齐次式的问题举例

1. 一次齐次分式

已知 $\tan \alpha =2$，求 $\frac{\cos \alpha +\sin \alpha }{\sin \alpha +\cos \alpha }$

步骤1：分式是关于 $\cos \alpha$ 与 $\sin \alpha$ 的，而已知的信息是 $\tan \alpha$，可以考虑用齐次式将分式变为关于 $\tan$ 的分式

步骤2：分式的分子分母都是多项式，并且多项式的每一项都是一次项，是齐次的，所以可以使用齐次式

步骤3：按照同角齐次式的理论，分子分母需要同除相同次数的 $\cos \alpha$，也就是一次式 $\cos \alpha$

步骤4：$\frac{(\cos \alpha +\sin \alpha )/\cos \alpha }{(\sin \alpha -\cos \alpha )/\cos \alpha }=\frac{\frac{\cos \alpha }{\cos \alpha }+\frac{\sin \alpha }{\cos \alpha }}{\frac{\sin \alpha }{\cos \alpha }-\frac{\cos \alpha }{\cos \alpha }}$ = $\frac{1+\tan \alpha }{\tan \alpha -1}$

步骤5：将 $\tan \alpha =2$ 代入，$\frac{1+\tan \alpha }{\tan \alpha -1}=\frac{1+2}{2-1}=3$

2. 二次齐次分式

已知 $\tan \alpha =2$，求 $\frac{3{\sin }^2\alpha +2\sin \alpha \cos \alpha }{4{\cos }^2\alpha -\sin \alpha \cos \alpha }$

步骤1：分式是关于 $\cos \alpha$ 与 $\sin \alpha$ 的，而已知的信息是 $\tan \alpha$，可以考虑用齐次式将分式变为关于 $\tan$ 的分式

步骤2：这里需要注意，两个三角函数相乘，可视为二次项，所以题中分式的分子分母中多项式的每一项都是二次项，是齐次的，可以使用齐次式

步骤3：按照同角齐次式的理论，分子分母需要同除相同次数的 $\cos \alpha$，也就是二次式 ${\cos }^2\alpha$

步骤4：$\frac{(3{\sin }^2\alpha +2\sin \alpha \cos \alpha )/{\cos }^2\alpha }{(4{\cos }^2\alpha -\sin \alpha \cos \alpha )/{\cos }^2\alpha }=\frac{\frac{3{\sin }^2\alpha }{{\cos }^2\alpha }+\frac{2\sin \alpha \cos \alpha }{{\cos }^2\alpha }}{\frac{4{\cos }^2\alpha }{{\cos }^2\alpha }-\frac{\sin \alpha \cos \alpha }{{\cos }^2\alpha }}=\frac{3{\tan }^2\alpha +2\tan \alpha }{4-\tan \alpha }$

步骤5：将 $\tan \alpha =2$ 代入，$\frac{3{\tan }^2\alpha +2\tan \alpha }{4-\tan \alpha }=\frac{3\ast (2{)}^2+4}{4-2}=8$

3. 非齐次分式

已知 $\tan \alpha =2$，求 $\frac{{\sin }^2\alpha +1}{\sin \alpha \cos \alpha +{\cos }^2\alpha }$

步骤1：先判断分子分母中多项式的每一项是否齐次，分母中多项式为 $\sin \alpha \cos \alpha$ 和 ${\cos }^2\alpha$ 都是二次项，分子中 ${\sin }^2\alpha$ 是二次项， $1$ 是一次项。所以这个分式不是齐次的

步骤2：将这种特殊分式变为齐次式，利用同角恒等式 ${\sin }^2\alpha +{\cos }^2\alpha =1$，将 $1$ 变成 ${\sin }^2\alpha +{\cos }^2\alpha$

步骤3：此时分式为 $\frac{{\sin }^2\alpha +{\sin }^2\alpha +{\cos }^2\alpha }{\sin \alpha \cos \alpha +{\cos }^2\alpha }$，分子分母中多项式的每一项都变为二次式了，满足齐次。后面就可以分子分母同除 ${\cos }^2\alpha$ 解分式了

4. 整式

已知 $\tan \alpha =2$，求 ${\sin }^2\alpha +\sin \alpha \cos \alpha$

步骤1：齐次式是将 $\cos \alpha$ 与 $\sin \alpha$ 的分式，变为关于 $\tan$ 的式子。而题中是一个整式，所以要先将其变为分式

步骤2：我们知道整式除 $1$ 值不变，所以可以将整式变为 $\frac{{\sin }^2\alpha +\sin \alpha \cos \alpha }{1}$，此时分子都是二次项但分母是一次项

步骤3：利用同角恒等式 ${\sin }^2\alpha +{\cos }^2\alpha =1$，将 $1$ 变成 ${\sin }^2\alpha +{\cos }^2\alpha$，变换后为 $\frac{{\sin }^2\alpha +\sin \alpha \cos \alpha }{{\sin }^2\alpha +{\cos }^2\alpha }$，分子分母的每一项都是二次项，是齐次，后面正常用齐次式的方式解就可以

2. 两角和与差公式

当不能单独使用诱导公式算出值时，可以考虑使用或搭配两角和与差公式

1. 正弦和与差公式

正弦和公式：$\sin (\alpha +\beta )=\sin \alpha \ast \cos \beta +\cos \alpha \ast \sin \beta$

正弦差公式：$\sin (\alpha -\beta )=\sin \alpha \ast \cos \beta -\cos \alpha \ast \sin \beta$

2. 余弦和与差公式

余弦和公式：$\cos (\alpha +\beta )=\cos \alpha \ast \cos \beta -\sin \alpha \ast \sin \beta$

余弦差公式：$\cos (\alpha -\beta )=\cos \alpha \ast \cos \beta +\sin \alpha \ast \sin \beta$

3. 正切和与差公式

正切和公式：$\tan (\alpha +\beta )=\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \ast \tan \beta }$

正切差公式：$\tan (\alpha -\beta )=\frac{\tan \alpha -\tan \beta }{1+\tan \alpha \ast \tan \beta }$

4. 例：求 $\sin (15^{\circ })$ 的值

解：

假设使用诱导公式，先将其变为 $(k\ast \frac{\pi }{2}+\alpha )$ 的形式，既 $\sin (0\ast \frac{\pi }{2}+15^{\circ })=\sin (15^{\circ })$，此时仍不能算出 $\sin (15^{\circ })$ 的值

这时就可以将 $15^{\circ }$ 变为 $45^{\circ }-30^{\circ }$，然后利用两角差公式计算， 即：$\sin (45^{\circ }-30^{\circ })=\sin 45^{\circ }\ast \cos 30^{\circ }-\cos 45^{\circ }\ast \sin 30^{\circ }=\frac{\sqrt{2}}{2}\ast \frac{\sqrt{3}}{2}-\frac{1}{2}\ast \frac{\sqrt{2}}{2}=\frac{\sqrt{6}-\sqrt{2}}{4}$

3. 辅助角公式

辅助角公式适合用来处理 $f(x)=a\sin \alpha +b\cos \alpha$ 的函数图像性质问题（最值、值域、单调性等）。

1. 公式

公式 1（常用）：将原式变为正弦两角和与差结构：

$f(x)=a\sin x+b\cos x=\sqrt{a^2+b^2}\ast \sin (x+\phi )$，其中 ($\tan \phi =\frac{b}{a}$)

公式 2：将原式变为余弦两角和与差结构：

$f(x)=a\sin x+b\cos x=\sqrt{a^2+b^2}\ast \cos (x-\phi )$，其中 ($\tan \phi =\frac{a}{b}$)

2. 以 <公式 1> 为例，演示公式的推导原理

推导思想：

因为 $f(x)=a\sin x+b\cos x$ 中有两个不同的三角函数，所以很难直接求出 $f(x)$ 的图像性质。公式的思想就是利用正弦两角和与差的结构，将原式变为 $A\sin (\omega \alpha +\phi )$ 的形式，这个形式就很容易解得图像性质。

推导过程：

目的：将原式变为正弦两角和与差的结构，即：$\sin \alpha \ast \cos \beta \pm \cos \alpha \ast \sin \beta$

实现：先对 $a\sin x+b\cos x$ 中的两个系数进行勾股运算，得到勾股数：$\sqrt{a^2+b^2}$

对原式的系数提取勾股数，即：$a\sin x+b\cos x=\sqrt{a^2+b^2}\ast (\frac{a}{\sqrt{a^2+b^2}}\ast \sin x+\frac{b}{\sqrt{a^2+b^2}}\ast \cos x)$

此时借助一个未知的辅助角 $\phi$，令：$\cos \phi =\frac{a}{\sqrt{a^2+b^2}}$

将 $\cos \phi$ 代入到式子中：$a\sin x+b\cos x=\sqrt{a^2+b^2}\ast (\cos \phi \ast \sin x+\frac{b}{\sqrt{a^2+b^2}}\ast \cos x)$

因为 $(\frac{a}{\sqrt{a^2+b^2}}{)}^2+(\frac{b}{\sqrt{a^2+b^2}}{)}^2=1$，所以 ${\cos }^2\phi +(\frac{b}{\sqrt{a^2+b^2}}{)}^2=1$

又因为同角三角函数恒等式 ${\cos }^2\alpha +{\sin }^2\alpha =1$，所以 $\frac{b}{\sqrt{a^2+b^2}}=\sin \phi$

将 $\sin \phi$ 代入到式子中：$a\sin x+b\cos x=\sqrt{a^2+b^2}\ast (\cos \phi \ast \sin x+\sin \phi \ast \cos x)$

此时小括号中的表达式已经满足两角和与差结构，整理后得：$a\sin x+b\cos x=\sqrt{a^2+b^2}\ast \sin (x+\phi )$

借助辅助角 $\phi$（未知角） 推导后，可以得到下面信息，后续利用这些信息求图像性质就容易了：

• 辅助角公式：$a\sin x+b\cos x=\sqrt{a^2+b^2}\ast \sin (x+\phi )$
• 关于 $\phi$ 的正弦等式：$\sin \phi =\frac{b}{\sqrt{a^2+b^2}}$
• 关于 $\phi$ 的余弦等式：$\cos \phi =\frac{a}{\sqrt{a^2+b^2}}$
• 关于 $\phi$ 的正切等式：因为同角三角函数恒等式 $\tan \alpha =\frac{\sin \alpha }{\cos \alpha }$，所以 $\tan \phi =\frac{\sin \phi }{\cos \phi }=\frac{b}{a}$
  
  

3. 例

求 $f(x)=12\sin x+5\cos x$ 的值域和周期？

解：

因为 $f(x)$ 中是两个三角函数的加减运算，所以不能直接求出其图像性质，因为是同角，所以可以借助辅助公式

直接套用辅助角公式，即：$\sqrt{12^2+5^2}\sin (x-\phi )=13\sin (x-\phi )$

原式变成 $A\sin (\omega x+\phi )$ 后，就可以按照以前学的正弦图像性质快速求出周期和值域

$\because A\sin (\omega x+\phi )$ 的周期为 $\frac{2\pi }{\omega }$

$\therefore 13\sin (x-\phi )$ 的周期为 $\frac{2\pi }{1}=2\pi$

$\because A\sin (\omega x+\phi )$ 的值域为 [$-A,A$]

$\therefore 13\sin (x-\phi )$ 的值域为 [$-13,13$]

4. 二倍角公式

1. 正弦二倍角公式

公式：$\sin 2\alpha =2\sin \alpha \cos \alpha$

公式推导：正弦的二倍角公式是基于正弦的两角和公式推导出来的，正弦两角和公式为：$\sin (\alpha +\beta )=\sin \alpha \ast \cos \beta +\cos \alpha \ast \sin \beta$ ，正弦二倍角无非就是 $\beta =\alpha$ 的特殊情况，即：$\sin (\alpha +\alpha )=\sin \alpha \ast \cos \alpha +\cos \alpha \ast \sin \alpha$，整理后得正弦二倍角公式：$\sin 2\alpha =2\sin \alpha \cos \alpha$

2. 余弦二倍角公式

公式 1：$\cos 2\alpha ={\cos }^2\alpha -{\sin }^2\alpha$

公式 1 推导：余弦的二倍角公式是基于余弦的两角和公式推导出来的，余弦两角和公式为：$\cos (\alpha +\beta )=\cos \alpha \ast \cos \beta -\sin \alpha \ast \sin \beta$ ，余弦二倍角无非就是 $\beta =\alpha$ 的特殊情况，即：$\cos (\alpha +\alpha )=\cos \alpha \ast \cos \alpha -\sin \alpha \ast \sin \alpha$，整理后余弦二倍角公式：$\cos 2\alpha ={\cos }^2\alpha -{\sin }^2\alpha$

公式 2：$\cos 2\alpha =2{\cos }^2\alpha -1$

公式 2 推导：公式 2 是在公式 1 的基础上利用同角三角函数恒等式 ${\sin }^2\alpha +{\cos }^2\alpha =1$ 推导出来的，这个恒等式可以变换成关于 ${\sin }^2\alpha$ 的等式 ${\sin }^2\alpha =1-{\cos }^2\alpha$，然后将 ${\sin }^2\alpha$ 代入到公式 1 中为：$\cos 2\alpha ={\cos }^2\alpha -(1-{\cos }^2\alpha )$，整理后得到公式 2 ：$\cos 2\alpha =2{\cos }^2\alpha -1$

公式 3：$\cos 2\alpha =1-2{\sin }^2\alpha$

公式 3 推导：公式 3 是在公式 1 的基础上利用同角三角函数恒等式 ${\sin }^2\alpha +{\cos }^2\alpha =1$ 推导出来的，这个恒等式可以变换成关于 ${\cos }^2\alpha$ 的等式 ${\cos }^2\alpha =1-{\sin }^2\alpha$，然后将 ${\cos }^2\alpha$ 代入到公式 1 中为：$\cos 2\alpha =1-{\sin }^2\alpha -{\sin }^2\alpha$，整理后得到公式 3 ：$\cos 2\alpha =1-2{\sin }^2\alpha$

3. 正切二倍角公式

公式：$\tan 2\alpha =\frac{2\tan \alpha }{1-{\tan }^2\alpha }$

公式推导：正切的二倍角公式是基于正切的两角和公式推导出来的，正切两角和公式为：$\tan (\alpha +\beta )=\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \ast \tan \beta }$ ，正切二倍角无非就是 $\beta =\alpha$ 的特殊情况，即：$\tan (\alpha +\alpha )=\frac{\tan \alpha +\tan \alpha }{1-\tan \alpha \ast \tan \alpha }$，整理后得正切二倍角公式：$\tan 2\alpha =\frac{2\tan \alpha }{1-{\tan }^2\alpha }$

5. 降幂公式

1. 正弦降幂公式

公式：${\sin }^2\alpha =\frac{1-\cos 2\alpha }{2}$

公式推导：正弦降幂公式是基于余弦的二倍角公式推导出来的，余弦的二倍角公式为：$\cos 2\alpha =1-2{\sin }^2\alpha$，整理成关于 $2{\sin }^2\alpha$ 的等式为：$2{\sin }^2\alpha =1-\cos 2\alpha$，然后去掉倍数 $2$，最后得到正弦降幂公式：${\sin }^2\alpha =\frac{1-\cos 2\alpha }{2}$

2. 余弦降幂公式

公式：${\cos }^2\alpha =\frac{1+\cos 2\alpha }{2}$

公式推导：余弦降幂公式是基于余弦的二倍角公式推导出来的，余弦的二倍角公式为：$\cos 2\alpha =2{\cos }^2\alpha -1$，整理成关于 $2{\cos }^2\alpha$ 的等式为：$2{\cos }^2\alpha =1+\cos 2\alpha$，然后去掉倍数 $2$，最后得到余弦降幂公式：${\cos }^2\alpha =\frac{1+\cos 2\alpha }{2}$

3. 同角不同三角函数相乘的降幂公式

公式：$\sin \alpha \cos \alpha =\frac{1}{2}\sin 2\alpha$

公式推导：公式是基于正弦的二倍角公式推导出来的，正弦的二倍角公式为：$\sin 2\alpha =2\sin \alpha \cos \alpha$，整理成关于 $2\sin \alpha \cos \alpha$ 的等式为：$2\sin \alpha \cos \alpha =\sin 2\alpha$，然后去掉倍数 $2$，最后得到公式：$\sin \alpha \cos \alpha =\frac{1}{2}\sin 2\alpha$

6. 半角公式（二倍角公式的变形）

1. 正弦半角公式

公式：$\sin \frac{\alpha }{2}=\pm \sqrt{\frac{1-\cos \alpha }{2}}$

公式推导：正弦半角公式是基于正弦降幂公式推导出来的，正弦降幂公式为：${\sin }^2\alpha =\frac{1-\cos 2\alpha }{2}$，先将 $\alpha$ 减半，得到等式：${\sin }^2\frac{\alpha }{2}=\frac{1-\cos \alpha }{2}$，最后开根后得到正弦半角公式 $\sin \frac{\alpha }{2}=\pm \sqrt{\frac{1-\cos \alpha }{2}}$

2. 余弦半角公式

公式：$\cos \frac{\alpha }{2}=\pm \sqrt{\frac{1+\cos \alpha }{2}}$

公式推导：余弦半角公式是基于余弦降幂公式推导出来的，余弦降幂公式为：${\cos }^2\alpha =\frac{1+\cos 2\alpha }{2}$，先将 $\alpha$ 减半，得到等式：${\cos }^2\frac{\alpha }{2}=\frac{1+\cos 2\alpha }{2}$，最后开根后得到余弦半角公式 $\cos \frac{\alpha }{2}=\pm \sqrt{\frac{1+\cos \alpha }{2}}$

3. 正切半角公式

公式 1：$\tan \frac{\alpha }{2}=\pm \sqrt{\frac{1-\cos \alpha }{1+\cos \alpha }}$

公式 1 推导：因为有同角恒等式 $\tan \alpha =\frac{\sin \alpha }{\cos \alpha }$，所以 $\tan \frac{\alpha }{2}=\frac{\sin \frac{\alpha }{2}}{\cos \frac{\alpha }{2}}$，分别用正弦半角和余弦半角公式进行替换得：$\tan \frac{\alpha }{2}=\frac{\pm \sqrt{\frac{1-\cos \alpha }{2}}}{\pm \sqrt{\frac{1+\cos \alpha }{2}}}=\pm \sqrt{\frac{(1-\cos \alpha )\ast \frac{1}{2}}{(1+\cos \alpha )\ast \frac{1}{2}}}=\pm \sqrt{\frac{1-\cos \alpha }{1+\cos \alpha }}$

公式 2：$\tan \frac{\alpha }{2}=\frac{\sin \alpha }{1+\cos \alpha }$

公式 2 推导：这个公式的目的是想将 $\tan \frac{\alpha }{2}$ 转换成关于 $\sin \alpha$ 和 $\cos \alpha$ 比值的等式，首先同样是因为有同角恒等式 $\tan \alpha =\frac{\sin \alpha }{\cos \alpha }$，所以 $\tan \frac{\alpha }{2}=\frac{\sin \frac{\alpha }{2}}{\cos \frac{\alpha }{2}}$，现在想把分子中的 $\sin \frac{\alpha }{2}$ 变成 $\sin \alpha$ 可以利用正弦二倍角公式：$\sin \alpha =2\sin \frac{\alpha }{2}\cos \frac{\alpha }{2}$，所以 $\sin \frac{\alpha }{2}$ 变成 $\sin \alpha$ 需要乘 $2\cos \frac{\alpha }{2}$，现在对分子分母同乘 $2\cos \frac{\alpha }{2}$，得到：$\tan \frac{\alpha }{2}=\frac{2\sin \frac{\alpha }{2}\cos \frac{\alpha }{2}}{2\cos \frac{\alpha }{2}\cos \frac{\alpha }{2}}$，整理后得：$\tan \frac{\alpha }{2}=\frac{\sin \alpha }{2{\cos }^2\frac{\alpha }{2}}$，现在再对分母进行处理，因为有余弦降幂公式为：${\cos }^2\alpha =\frac{1+\cos 2\alpha }{2}$，所以 ${\cos }^2\frac{\alpha }{2}=\frac{1+\cos \alpha }{2}$，在乘倍数 $2$ 得：$2{\cos }^2\frac{\alpha }{2}=1+\cos \alpha$，最后将 $1+\cos \alpha$ 代回到分母即可得到公式：$\tan \frac{\alpha }{2}=\frac{\sin \alpha }{1+\cos \alpha }$

公式 3：$\tan \frac{\alpha }{2}=\frac{1-\cos \alpha }{\sin \alpha }$

公式 3 推导：这个公式的目的是想将 $\tan \frac{\alpha }{2}$ 转换成关于 $\cos \alpha$ 和 $\sin \alpha$ 比值的等式，首先同样是因为有同角恒等式 $\tan \alpha =\frac{\sin \alpha }{\cos \alpha }$，所以 $\tan \frac{\alpha }{2}=\frac{\sin \frac{\alpha }{2}}{\cos \frac{\alpha }{2}}$，现在想把分母中的 $\cos \frac{\alpha }{2}$ 变成 $\sin \alpha$ 可以利用正弦二倍角公式：$\sin \alpha =2\sin \frac{\alpha }{2}\cos \frac{\alpha }{2}$，所以 $\cos \frac{\alpha }{2}$ 变成 $\sin \alpha$ 需要乘 $2\sin \frac{\alpha }{2}$，现在对分子分母同乘 $2\sin \frac{\alpha }{2}$，得到：$\tan \frac{\alpha }{2}=\frac{2\sin \frac{\alpha }{2}\sin \frac{\alpha }{2}}{2\cos \frac{\alpha }{2}\sin \frac{\alpha }{2}}$，整理后得：$\tan \frac{\alpha }{2}=\frac{2{\sin }^2\frac{\alpha }{2}}{\sin \alpha }$，现在再对分子进行处理，因为有正弦降幂公式为：${\sin }^2\alpha =\frac{1-\cos 2\alpha }{2}$，所以 ${\sin }^2\frac{\alpha }{2}=\frac{1-\cos \alpha }{2}$，在乘倍数 $2$ 得：$2{\sin }^2\frac{\alpha }{2}=1-\cos \alpha$，最后将 $1-\cos \alpha$ 代回到分子即可得到公式：$\tan \frac{\alpha }{2}=\frac{1-\cos \alpha }{\sin \alpha }$

7. 万能公式

1. 正弦万能公式

公式：$\sin 2\alpha =\frac{2\tan \alpha }{1+{\tan }^2\alpha }$

公式推导：这个公式用来转换正弦二倍角和正切一倍角，公式的推导主要利用了正弦二倍角公式和同角齐次式，首先正弦二倍角公式为：$\sin 2\alpha =2\sin \alpha \cos \alpha$，然后利用同角齐次式将其变为：$\sin 2\alpha =\frac{(2\sin \alpha \cos \alpha )\ast \frac{1}{{\cos }^2\alpha }}{({\sin }^2\alpha +{\cos }^2\alpha )\ast \frac{1}{{\cos }^2\alpha }}=\frac{\frac{2\sin \alpha }{\cos \alpha }}{\frac{{\sin }^2\alpha }{{\cos }^2\alpha }+\frac{{\cos }^2\alpha }{{\cos }^2\alpha }}=\frac{2\tan \alpha }{{\tan }^2\alpha +1}$

2. 余弦万能公式

公式：$\cos 2\alpha =\frac{1-{\tan }^2\alpha }{1+{\tan }^2\alpha }$

公式推导：这个公式用来转换余弦二倍角和正切一倍角，公式的推导主要利用了余弦二倍角公式和同角齐次式，首先余弦二倍角公式为：$\cos 2\alpha ={\cos }^2\alpha -{\sin }^2\alpha$，然后利用同角齐次式将其变为：$\cos 2\alpha =\frac{({\cos }^2\alpha -{\sin }^2\alpha )\ast \frac{1}{{\cos }^2\alpha }}{({\sin }^2\alpha +{\cos }^2\alpha )\ast \frac{1}{{\cos }^2\alpha }}=\frac{\frac{{\cos }^2\alpha }{{\cos }^2\alpha }-\frac{{\sin }^2\alpha }{{\cos }^2\alpha }}{\frac{{\sin }^2\alpha }{{\cos }^2\alpha }+\frac{{\cos }^2\alpha }{{\cos }^2\alpha }}=\frac{1-{\tan }^2\alpha }{{\tan }^2\alpha +1}$

三、反三角函数

高中阶段的反三角函数简单了解其图像性质即可

1. 反正弦函数

反正弦函数记做：$y=\arcsin x$

反正弦函数图像：正弦函数图像中，取定义域 $x$ 为 $[-\frac{\pi }{2},\frac{\pi }{2}]$ 的这一段，然后将图像关于 $y=x$ 对称（关于 $y=x$ 对称，即原图像的 $x$ 就是新图像的 $y$，原图像的 $y$ 就是新图像的 $x$），这时的图像就是反正弦函数图像。

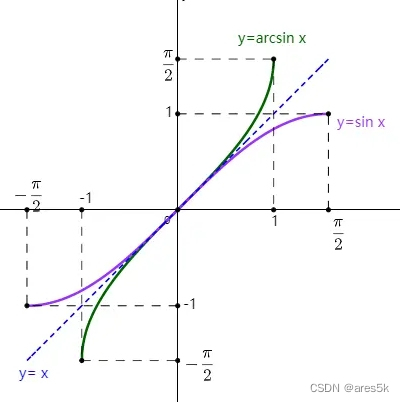
反正弦函数的图像性质：

• 定义域：$[-1,1]$
• 值域：$[-\frac{\pi }{2},\frac{\pi }{2}]$
• 单调性：单调递增
• 奇偶性：关于原点对称，所以是奇函数
  
  

2. 反余弦函数

反余弦函数记做：$y=\arccos x$

反余弦函数图像：余弦函数图像中，取定义域 $x$ 为 $[0,\pi ]$ 的这一段，然后将图像关于 $y=x$ 对称（关于 $y=x$ 对称，即原图像的 $x$ 就是新图像的 $y$，原图像的 $y$ 就是新图像的 $x$），这时的图像就是反余函数弦图像。

反余弦函数的图像性质：

• 定义域：$[-1,1]$
• 值域：$[0,\pi ]$
• 单调性：单调递减
• 奇偶性：既不关于原点对称，也不关于 $y$ 轴对称，是一个非奇非偶函数
  
  

3. 反正切函数

反正切函数记做：$y=\arctan x$

反正切函数图像：正切函数图像中，取定义域 $x$ 为 $(-\frac{\pi }{2},\frac{\pi }{2})$ 的这一段，然后将图像关于 $y=x$ 对称（关于 $y=x$ 对称，即原图像的 $x$ 就是新图像的 $y$，原图像的 $y$ 就是新图像的 $x$），这时的图像就是反正切数弦图像。

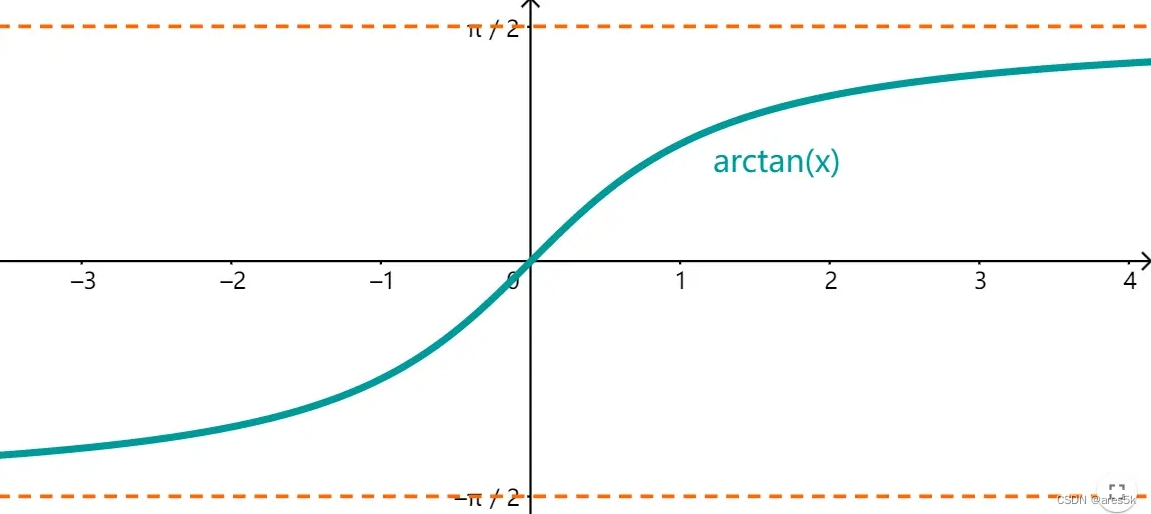
反正切函数的图像性质：

• 定义域：$(-\infty ,\infty )$
• 值域：$(-\frac{\pi }{2},\frac{\pi }{2})$
• 单调性：单调递增
• 奇偶性：关于原点对称，所以是奇函数